Некласична математична логіка

Розділ 5

Нечітка логіка

Логіка у звичайному сенсі слова є уявленням механізму мислення, повинна бути завжди строго формалізованою. Однак у дійсності існує не одна логіка (наприклад, булева), а стільки, скільки ми побажаємо, тому що все визначається вибором відповідної системи аксіом. Звичайно, як тільки аксіоми прийняті, всі твердження, що побудовані на їх основі, повинні бути строгими, без суперечності, пов'язані за правилами, встановленими в цій системі аксіом.

Нечітка логіка є узагальненням класичної логіки на випадок, коли істинність розглядається як лінгвістична змінна, що набуває значення типу: "дуже істинно", "більш-менш істинно", "не дуже хибно" і т. п. Зазначені лінгвіст-тичні значення представляються нечіткими множинами. Основна відмінність від класичної логіки полягає в тому, що замість значень “істина“ і “хибність“ у нечіткій логіці використовується ступінь істинності, що набуває значення з нескінченної множини від 0 (хибність) до 1 (істина) включно. Отже, логічні операції вже не можуть бути подані таблицями істинності. У нечіткій логіці вони задаються функціями і лише в крайніх випадках ‒ коли значення змінних виключно 1 або 0 ‒ згадані вище функції дають таблиці істинності операцій класичної логіки.

Основи нечіткої логіки були закладені в кінці 1960-х років у працях відомого американського математика Лотфі А. Заде, що започаткував теорію нечітких множин. Термін "нечітка логіка" використовується зазвичай у двох різних значеннях. У вузькому сенсі нечітка логіка ‒ це логічне числення, що є розширенням багатозначної логіки. В її широкому сенсі, який сьогодні є переважаючим у використанні, нечітка логіка рівнозначна теорії нечітких множин. З цієї точки зору нечітка логіка у вузькому сенсі є розділом нечіткої логіки в широкому сенсі.

5.1. Основні визначення

Означення 5.1.1. Нечіткою множиною з універсальної множини U називають сукупність упорядкованих пар = {(_х(а), а): а U }, де _х(а) ‒ функція належності нечіткої множини (_х : U[0, 1]), що приписує кожному елементу а U ступінь його належності .

Використовують спеціальний запис нечітких множин. Якщо U є універсумом зі скінченною кількістю елементів, то можна подати так:

. (5.1)

Якщо U є нескінченною множиною, то записують так:

. (5.2)

Знаки  і  у формулах (5.1) та (5.2) мають інтерпретацію множини елементів. Характерні також табличний та графічний спосіб подання .

Приклад 5.1.1. Визначити за допомогою нечіткої множини поняття ”людина середнього зросту ” , задавши універсум множиною U = {150, 155, 160,… 190} (зріст заданий у см).

Розв’язання. Виходячи з умови, з позицій першого дослідника це поняття може бути визначеним такою нечіткою множиною:

.

Інший дослідник, вважаючи, що людина має середній зріст 175 ‒ 180 см, подасть шуканий результат іншою нечіткою множиною:

.

Приклад 5.1.2. Введемо означення нечітких множин : ‒ “малий зріст людини”, ‒ “середній зріст людини”, ‒ “великий зріст людини”. Як універсум застосуємо U = {xR : 0 ≤ x ≤ a_max }, де a_max – можливий максимальний зріст людини в см.

На рис. 5.1 подано графіки функцій належності, що визначають уведені множини.

Рисунок 5.1 – Графіки функцій належності множин , , .

У точці а = 175 см, _x(a) = _y(a) =0,5, тоді як _z(a) = 0.

Функції належності зручно задавати в параметричній формі. Найбільшу популярність отримали трикутна, трапецевидна, гаусова, сигмоїдальна та Пі-подібна функції належності.

Рисунок 5.2 – Види графіків функцій належності (в порядку слідування: Z – функція; П ‒ функція; Л ‒ функція; S ‒ функція)

Для побудови функцій належності можна використати метод, що базується на статистичній обробці думок групи експертів. У наведених вище прикладах використані прямі методи, коли експерт або просто задає для будь-якого а U значення _x(a), або визначає функцію належності. Як правило, прямі методи задання функції належності використовуються для вимірних понять, таких як швидкість, година, відстань, тиск, температура і так далі, тобто коли виділяються полярні значення.

Непрямі методи визначення значень функції належності використовуються у випадках, коли немає елементарних вимірних властивостей для визначення нечіткої множини. Як правило, це методи попарних порівнянь.

Означення 5.1.2. Висотою нечіткої множини називають величину .

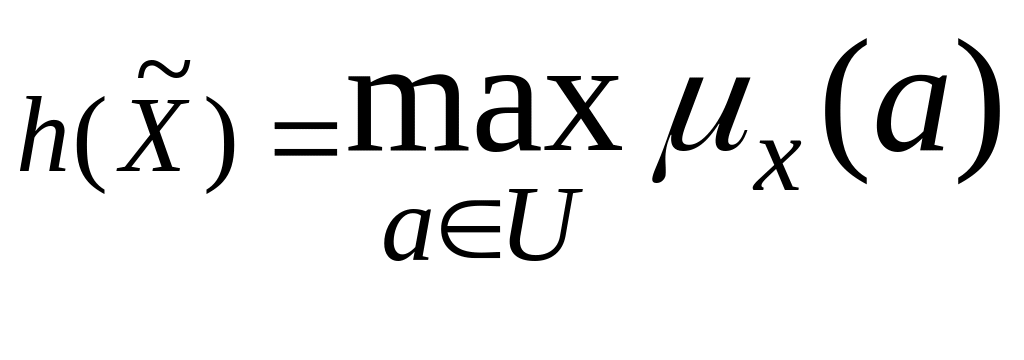Приклад 5.1.3. Якщо U = {2, 3, 4, 5, 6}, a , то висотою нечіткої величини буде .

Означення 5.1.3. Нечітку множину називають нормальною, якщо . Якщо множина не є нормальною, то нормалізацію нечіткої множини можна провести за правилом , де вже стає нормальною нечіткою множиною.

Приклад 5.1.4. Нечітку множину прикладу 5.1.3 нормалізувати.

Розв’язання. За означенням 5.1.3 одержимо .

Означення 5.1.4. Нечітку множину називають субнормальною, якщо h( ) < 1 .

Означення 5.1.5. Нечітку множину називають порожньою, якщо _х(а) = 0 для всіх а U.

Означення 5.1.6. Нечітка множина називається унімодальною, якщо _х(а) = 1 лише для одного елемента з U.

Означення 5.1.7. α-перерізом нечіткої множини називають множину Х_α ={aU: _х(а) ≥ α} (α[0,1]). Множина Х_α належить до звичайних (чітких) множин.

Приклад 5.1.5. Для заданої універсальної множини U = {0,1,2..,10} і нечіткої множини

= визначити Х_0,6 і Х_1.

Розв’язання. Виходячи з означення 5.1.5,

Х_0,6 ={4,5,6,7,8}; Х₁ ={5,6}.

Означення 5.1.8. Лінгвістичною змінною називається змінна, значеннями якої можуть бути слова або словосполучення деякої природної або штучної мови.

Означення 5.1.9. Терм-множиною називається множина всіх можливих значень лінгвістичної змінної.

Означення 5.1.10. Термом називається будь-який елемент терм-множини. В теорії нечітких множин терм формалізується нечіткою множиною за допомогою функції належності.

Приклад 5.1.6. Розглянемо змінну “швидкість автомобіля“, що оцінюється за шкалою “низька“, “середня“, “висока“ і “дуже висока“.

У цьому прикладі лінгвістична змінна є “швидкість автомобіля“, термами ‒ лінгвістичні оцінки “низька“, “середня“, “висока“ і “дуже висока“, які й становлять терм-множину.

Означення 5.1.11. Фаззіфікацією називається процедура перетворення чітких даних у нечітку множину.

Не вдаючись у подробиці, процедура фаззіфікації виявляється у формалізації даних як лінгвістичних змінних, введення всіх можливих термів, що їх характеризують, та побудові функцій належності для кожного терма.

Означення 5.1.12. Дефаззіфікацією (в нечіткій логіці) називається процедура перетворення нечіткої множини в чітке число.

У теорії нечітких множин процедура дефаззіфікації аналогічна знаходженню характеристик становища (математичного сподівання, моди, медіани) випадкових величин у теорії ймовірності. Наприклад, таким числом може стати максимум функції належності, центр ваги функції належності чи щось інше.