Коледж КНУТД Математика І курс_дистанційне навчання

Модуль 5 Вектори і координати зм 13 Прямокутні координати у просторі.

Мета: сформувати уявлення про декартові координати у просторі, перетворення фігур у просторі та їх властивості, поняття кутів між мимобіжними прямими, між прямою та площиною, між площинами, вміння знаходити відстань між точками, координати середини відрізка, навчитися застосовувати набуті знання до розв'язування задач,виховувати дисциплінованість, здібності до самоорганізації, самоосвіти.

1. Опорні питання заняття:

1. Введення декартових координат у просторі.

2. Відстань між точками. Координати середини відрізка.

3. Перетворення фігур у просторі.

4. Кути у просторі.

2. Запитання для самоперевірки

3. Задачі

Ключові поняття: координати точки, відстань, середина відрізка, симетрія, рух, паралельне перенесення, перетворення подібності, кут між мимобіжними прямими, кут між прямою і площиною, кут між площинами, ортогональна проекція

Література:

• Погорєлов О.В. Стереометрія: Підруч. для 10-11 кл. серед. шк.

• Бевз Г.П. та ін. Геометрія: Підруч. для 10-11 кл. загальноосв.навч.закл.

1. Опорні питання заняття:

   1. Введення декартових координат у просторі.

Координатна пряма – .

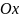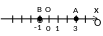Обов'язково має напрям (додатний) у сторону збільшення числових значень, початок координат (точка 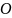) та масштабну одиницю.

Точки, які лежать на цій прямій мають лише одну координату – абсцису : , , .

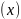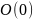Координатна площина – .

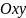Представляє собою 2 взаємно перпендикулярні координатні прямі, початки яких збігаються, а також здебільшого однакові масштабні одиниці.

Осі розбивають координатну площину на 4 частини – квадранти.

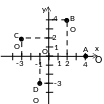Точки, розміщені на площині, мають 2 впорядковані координати – абсцису та ординату : .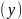

Початок координат – точка .

Точка лежить на осі , тому у неї ненульова тільки перша координата – абсциса. Аналогічно, у точок, які лежать на осі ненульовими будуть тільки другі координати – ординати.

Знайдіть самостійно координати двох інших точок на зображенні.

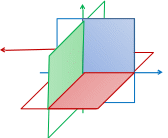Перевірте себе: ,

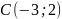Координатний простір – Oxyz.

Якщо взяти три взаємно перпендикулярні координатні прямі – (вісь абсцис), (вісь ординат) та 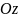(вісь аплікат), які перетинаються в одній точці 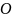(початок координат), то вони утворять взаємно перпендикулярні координатні площини – , , .

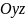Осі розбивають координатний простір на 8 частин, які називають октантами.

Точка розбиває осі на півосі: додатну і від'ємну.

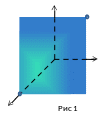
Візьмемо довільну точку 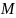і проведемо через неї площину, паралельну координатній площині . Вона перетне вісь в деякій точці 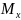(рис 1).

Координатою (або абсцисою) точки називається число, яке дорівнює за абсолютною величиною довжині відрізка : додатне, якщо точка лежить на додатній півосі , від'ємне, якщо вона лежить на від'ємній півосі і дорівнює нулю, якщо точка збігається з точкою .

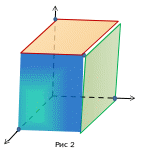
Проведемо через точку ще дві площини, паралельні відповідно координатним площинам та . Вони перетнуть відповідні осі координат – у точці 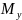та – у точці 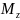(рис 2).

Координати точки у просторі позначають так: 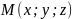, а іноді використовують просто координати, без буквених позначень.