Основные положения метода конечных элементов

Для обеспечения необходимой прочности элементов и узлов машины центробежного торкретирования, обеспечивающих надежную работу при минимальном расходе материалов необходимо исследование напряженно- деформированного состояния конструкции. Это позволяет обеспечить более высокую точность расчетов конструкции на прочность и обеспечить ее долговечность.

В качестве одного из наиболее эффективных методов расчета прочности сложных конструкций следует отметить метод конечных элементов .

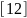С появлением мощных ПЭВМ возможности этого метода становятся практически неограниченными.

Напряженно-деформированное состояние элементов и узлов МЦТ в зависимости от нагрузки на них и характеристик материалов, из которых они изготовлены можно описать дифференциальными уравнениями, любое из которых может быть получено из общего квазигармонического уравнения.

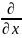
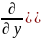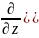)+ )+ )+Q= 0 (4)

где х, у,z – пространственные координаты;

u- искомая непрерывная функция;

, – коэффициенты, описывающие свойства объекта;

Q- внешнее воздействие.

При решении задач упругости вместо приведенного уравнения часто применяют вариационный подход, пологая, что решение для искомой функции и совпадает с функцией, минимизирующий функционал. Это предполагает определенную последовательность приведения расчетов по МКЭ.

1)Первым шагом на пути решения поставленной задачи является разбиение области решения на конечные элементы. Методика разбиения области зависит от имеющихся инженерных навыков и опыта компьютерного моделирования.

Выбор типа, формы элементов и числа его узловых точек зависит, от характера рассматриваемой задачи и от точности решения, которую требуется обеспечить. Вместе с тем, при замене исходного технического объекта его дискретной моделью необходимо обеспечить как можно большую идентичность в поведении аналога и модели.

2) В качестве основных неизвестных при использовании метода конечных элементов принимаются узловые значения искомой функции, и ее частные производные до m- го порядка. Общее число неизвестных определяет число степеней свободы, а то последнего зависит точность определения искомой функции в объеме каждого конечного элемента, и, следовательно, во всей области поставленной задачи.

После выбора узловых неизвестных строится аппроксимирующий полином, который выражает закон изменения искомой функции u (x, y, z) по объему конечного элемента через значения его узловых неизвестных. Модельно искомой функции является система

u (x, y, z)= = [N] {𝛿}, (5)

где М- число конечных элементов дискретной модели;

[N]= {[N] ⁽¹⁾ [N] ⁽²⁾ … [N] ⁽ⁿ⁾},

{σ}- вектор узловых неизвестных для всей совокупности конечных элементов.

[N] ^(е)- матрица - строка, элементы которой называются функциями формы конечного элемента;

{𝛿}^(е)- вектор узловых неизвестных е- го конечного элемента.

Следует отметить, что полученные полиномы всегда должны обеспечивать непрерывность искомой функции u (x, y, z) и ее производных до (m-1)- го порядка включительно по всей области решения. В каждом из полиномов должны содержаться члены, обеспечивающие их переход к постоянным значениям при уменьшении размеров конечного элемента.

3) Основным этапом моделирования является получение основной системы разрешающих уравнений. В общем случае вектор {𝛿} неизвестен. В вариационном методе конечных элементов алгоритм получения основной системы разрешающих уравнений основан на минимизации функционала.

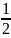
F= {ε}^т {σ} dV – {f}^т {p}dV-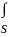 {f}^т {g} dS , (6)

где F- потенциальная энергия;

V- объем тела;

{σ}- вектор- столбец напряжений;

S- граница тела;

{f}- вектор- столбец перемещений тела;

{p}- распределенные массовые силы;

{g}- распределенная внешняя нагрузка.

Решение данного алгоритма состоит из четырех этапов.

На первом этапе осуществляется выбор функционала F, который является суммой соответствующих функционалов, относящихся к отдельным конечным элементам.

На втором этапе осуществляется подстановка аппроксимирующего выражения 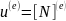{𝛿}^(е) в уравнение функционала 6 и получение элементных вкладов в функционал F.

На третьем этапе осуществляется минимизация по вектору{𝛿} функционала F. Для этого составляется уравнения

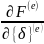= 0 (7)

Суммирование этих уравнений по конечным элементам приводит к системе алгебраических уравнений

[К] {𝛿}= {R}, (8)

где [К]- матрица жесткости системы элементов;

{R}- вектор нагрузки.

И, наконец, на четвертом этапе решение системы 5 позволяет определить неизвестный вектор узловых значений.