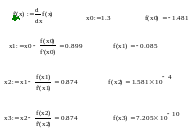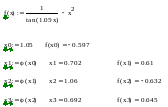Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «московский технический университет связи и информатики»

2. Курсовая работа

по дисциплине «Информатика»

по теме

«Модели и алгоритмы решения задач численными методами»

Вариант № 44

Студент гр. 2БШИ1401 Куратов А.А.

Преподаватель ____________/ Сосновиков Г.К./

Москва 2014

Тема 1. Решение алгебраических и трансцендентных уравнений Решение задачи на практических занятиях

Задание. Выбрать нелинейное уравнение из табл. и затем:

• отделить корень уравнения.

• проверить выполнение условий сходимости (в методе итераций, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости);

• выбрать начальное приближение

1. Отделение корня уравнения.

2. Уточнение корня уравнения

Результаты расчета для трех итераций (метод половинного деления).

Результаты расчета для трех итераций (метод Ньютона).

«Ручной расчет» трех итераций

Представим вычисления в виде следующей табл. 1.2-2b.

k	Xk	f(xk)
0	1.3	-1.481
1	0.899	-0.085
2	0.874	1.581*10-4
3	1.874	7.205*10-10

Домашняя работа

Результаты расчета для трех итераций (метод итераций).

Для сходимости метода необходимо представить уравнение f(x)=0 в виде x=φ(x). Для сходимости метода необходимо, чтобы первая производная от функции φ(x) была по модулю <1.

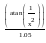
Приведем уравнение f(x)=0к виду x = и проведем исследование.

Выберем начальное значение (в методе итерацийx0– произвольное значение из отрезка [a;b]), например, x0=1.3, и с использованием итерационной функции выполним три итерации.

2. «Ручной расчет» трех итераций

Тема 2. Технология вычисления интегралов в среде

математических пакетов

Задание: вычислить интеграл заданными методами.

В домашней работе вычислить интеграл из своего индивидуального задания третьим методом (например, если в лабораторной работе использовались методы средних прямоугольников и трапеций, то использовать метод Симпсона и т.д.)

Решение задачи на практических занятиях

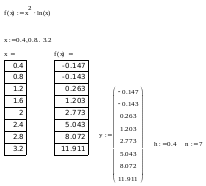
• определенный интеграл ;

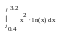• шаг интегрирования h=0.4.

Вычисление определенного интеграла

Получение таблицы значений подынтегральной функции

Интегрирование с использованием численных методов

Метод трапеций

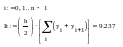
Метод Симпсона

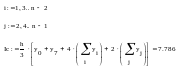
Домашняя работа

Метод средних прямоугольников

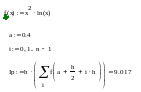
Тема 3. Технология решения задач одномерной

оптимизации средствами математических

пакетов

Задание.

• построить график функции f(x), выбрать отрезок, содержащий минимум, и проверить на нем условие унимодальности функции;

• Провести «ручной расчет» 3-х итераций по поиску минимума функции f(x) на отрезке [a;b], в соответствии с заданным методом.

В домашней работе вычислить минимум вторым (не использующимся в лабораторной работе) методом.

Решение задачи на практических занятиях

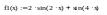
Решения задач средствами пакета Mathcad

Отделение отрезка унимодальности Первая производная не убывает, а вторая - положительна следовательно, на отрезке [0;2] существует единственный минимум

Метод дихотомии