44. Аналитические показатели динамического ряда, способы их расчета и взаимосвязь.

При изучении динамики общественных явлений рассчитывают следующую систему аналитических показателей: абсолютные приросты, темпы роста, темпы прироста и абсолютное значение одного процента прироста либо снижения. Расчет этих показателей основан на абсолютном или относительном сравнении уровней динамического ряда. При этом если каждый уровень сравнивается с его предыдущим уровнем, получают цепные показатели, а если каждый уровень сравнивается с начальным или каким-нибудь другим, принятым за постоянную базу сравнения, то получают базисные показатели динамики.

Абсолютный прирост – это разность двух уровней ряда динамики. Он показывает, на сколько абсолютных единиц данный уровень больше или меньше уровня, взятого для сравнения, и выражается в тех же единицах, что и уровни анализируемого ряда. Цепной абсолютный прирост исчисляется как разность между сравниваемым уровнем и предшествующим ему уровнем

Базисный абсолютный прирост исчисляется как разность между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения

Абсолютный прирост может иметь + ил – знак, в последнем случае это не прирост, а снижение.

Темп роста – это отношение двух уровней ряда динамики. Он выражается в коэффициентах или в процентах. В первом случае он показывает, во сколько раз данный уровень больше или меньше уровня, взятого для сравнения, во втором – сколько процентов данный уровень составляет по отношению к другому уровню, взятому для сравнения. Цепной темп роста исчисляется как отношение между сравниваемым уровнем и предшествующим ему уровнем

Базисный темп роста исчисляется как отношение между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения

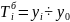
Если темп роста меньше единицы, то имеет место не рост, а снижение анализируемого уровня.

Темп прироста – это отношение абсолютного прироста к уровню, принятому за базу сравнения. Он обычно выражается в % и показывает, на сколько % уровень данного периода больше или меньше базисного. Цепной темп прироста

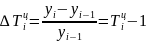
Базисный тем прироста 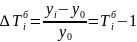. Темп прироста вычисляется и как разность между темпом роста, выраженным в %, и 100 %

Темп прироста может иметь как + так и – знак.

Абсолютное значение 1 % прироста – это отношение цепного абсолютного прироста за анализируемый период к соответствующему темпу прироста, выраженному в %

Следовательно, количественно абсолютное значение 1% равно одной сотой части уровня, предшествующего анализируемого, и выражается в тех же единицах, что и соответствующие уровни.

45. Средние показатели динамического ряда и методы их расчёта.

Статистические хар-ки динамики могут меняться во времени и варьируют по годам. Для получения обобщающей хар-ки динамики изучаемых явлений рассчитывается ср показатели динамики.

1. Ср-й уровень ряда хар-ет типичную величину абсолют-х уровней. Он рассчитывается:

а) в интервальном ряду – по формуле средней арифметической простой:

где у – уровни интервального ряда, n – количество равных периодов времени

б) в моментном динамическом ряду с равными промежутками времени между датами – по формуле средней хронологической простой:

в) в моментном ряду с неравными промежутками времени между 2-мя датами – по формуле средней арифметической взвешенной:

2. Средний абсолютный прирост – обобщающий показатель скорости абсолютного изменения уровней динамического ряда, т.е. он показывает на сколько единиц изменится уровень в среднем за единицу времени, всегда является интервальным показателем. Рассчитывается по формуле:

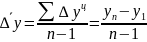
n-число уровней ряда динамики, n-1- число цепных абсолютных приростов

3. Средний темп роста – обощающая характеристика индивидуальных темпов роста ряда динамики:

где m=n-1 – число цепных темпов роста.

Если расчёт ведётся по периодам разной продолжительности, пользуются средними геометрическими взвешенными по продолжительности периодов:

где t_i – продолжительность i-тых отрезков времени.

4. Средний темп прироста является обобщающим показателем темпов роста уровней ряда динамики. Выражается в процентах, показывает на сколько процентов увеличился (или уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени.

(если выражен в коэффициентах)

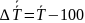(если выражен в процентах)