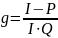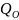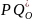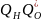Билет №9

1. Эффективность контроля цу.

Контроль ЦУ необходим для повышения надёжности их работы и повышения вероятности получения правильной информации, поступающей с цифрового устройства.

Оценка эффективности нужна для сравнения различных методов контроля. А для этого необходимо установить соответствие между надёжностью и характеристиками контроля (достоверность, полнота и так далее). Надёжность ЦУ оценивается как вероятность безотказной работы P(t).

Если неисправность возникает в момент ϴ и если ϴ>t, то считается, что на интервале 0 устройство работает безотказно. (Вероятность P(t)).

Тогда P(t) можно считать как вероятность получения правильной информации.

1-P(t) – вероятность получения ложной информации.

При отказе мы не получаем информации или полученная информация неправильная.

Q(t) – вероятность получения неправильной информации.

Картинка соотношения времён функционирования

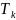- период функционирования ДУ;

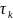– длительность контроля;

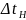- время существования неисправности;

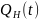- ошибка ЦУ не будет обнаружена;

- ошибка ЦУ будет обнаружена;

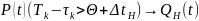
Δt_H

ϴ t

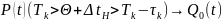
t > t

ϴ

t < t

ϴ

ϴ

Q(t) = Q₀(t) + Q_H(t)

P(t) – вероятность того, что ошибки нет.

P(t) + Q₀(t) + Q_H(t) = 1 – полная группа событий ЦУ.

ЦУ выдаёт информацию в соответствии с вероятностями.

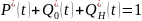- полная группа событий относится к СК.

СК – система контроля.

ЦУ СК	Исправен Р	Не исправен, ошибка не обнаружена	Не исправен, ошибка обнаружена
Исправен Р*	РР*
Не исправен, ошибка не обнаружена
Не исправен, ошибка обнаружена

Вероятность получения правильной информации:

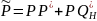
Вероятность получения ложной информации:

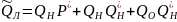
Вероятность отсутствия информации (информация не будет получена, СК выдаёт сообщение об ошибке):

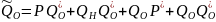
Полная группа событий:

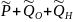
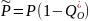
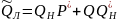
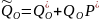
Эффективность контроля цу

Она показывает, насколько ОК соответствует своему назначению (а именно – выдавать информацию).

Эффективность – вероятность получения правильной информации при условии её получения.

Критерий эффективности должен учитывать два фактора:

• Качество метода контроля;

• Качество контрольной аппаратуры;

Обозначим эффективность: I

- правильное;

Из предыдущих выражений видно, что контроль увеличивает вероятность получения правильной информации и уменьшает вероятность получения неправильной информации (СК отсеивает часть ложной информации, но и часть правильной информации).

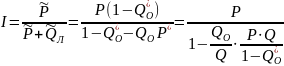
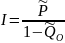
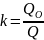– качество метода контроля;

- качество контрольной аппаратуры;

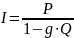- эффективность контроля;

g = k * h – качество контроля;

обычно при проектировании СК задаются I, P, Q.

Если I, P, Q заданы, то качество контроля выражается формулой: