
- •Список сокращений
- •Билет №1
- •Аналитические модели ду.
- •3.Покрытие ду
- •Разделимые арифметические коды.
- •Билет №2
- •Структурно – аналитическая модель ду.
- •Понятие кодового расстояния и его использование в теории кодирования.
- •Билет №3
- •Активизация одномерного пути.
- •Понятие тестов ду (контролирующие, диагностические).
- •Билет №4
- •Метод эквивалентной нормальной формы.
- •Порождающая и проверяющая матрицы.
- •Билет №5
- •Метод булевой разности.
- •Контроль озу. Аппаратно микропрограммный контроль
- •Билет №6
- •Элементы теории линейного кодирования.
- •Контроль мажоритарно – резервированных элементов.
- •Билет №7
- •Циклические коды.
- •Контроль с использованием квазислучайных последовательностей. Билет №8
- •Сигнатурный анализ (сигнатурный анализ в контроле).
- •Определение сверток двоичного слова.
- •Билет №9
- •Эффективность контроля цу.
- •Картинка соотношения времён функционирования
- •Эффективность контроля цу
- •Тест процедуры.
- •Билет №10
- •Коррекция арифметических операций.
- •Понятие свёртки. Вычисление свёртки двоичного числа
- •Билет №11
- •Числовой аппаратный контроль по модулю.
- •Структурная модель ду.
- •Билет №12
- •Цифровой контроль по модулю.
- •Принцип коррекции искажений.
- •Билет №13
- •Соотношение между надёжностью цу и систем контроля.
- •Теоретические предпосылки контроля по модулю 2 (контроль по четности) и определение искаженного разряда.
Список сокращений
АЛУ – арифметические логические устройства;
вч – вычитание;
ДНФ – дизъюнктивная нормальная область;
ДУ – дискретное устройство;
ЗП – записывается;
ЗУ – запоминающее устройство;
Инв – инверт;
ИР – информационные разряды;
КР – контрольные разряды;
КЦУ – контроль цифрового устройства;
МЭ – мажоритарный элемент;
НР – неработоспособное;
ОЗУ – оперативное запоминающее устройство;
ОК – объект контроля;
ПДУ – последовательное дискретное устройство;
Р – работоспособное;
Рг – регистр;
св – свёртка;
СК – система контроля;
СМ – сумматор;
СО – сигнал ошибки;
СЧ – считывание;
УКр – устройство коррекции;
УПР – устройство переключения режимов;
УС – устройство сравнения;
ФЭ – функциональный элемент;
ЦУ – цифровое устройство;
ЭА – элемент анализа;
ЭНФ – эквивалентная нормальная форма;
Оглавление
Билет №1 2
Билет №2 5
Билет №3 7
Билет №4 10
Билет №5 13
Билет №6 15
Билет №7 18
Билет №8 20
Билет №9 21
Билет №10 25
Билет №11 27
Билет №12 30
Билет №13 33
Билет №1
Аналитические модели ду.
Уравнение непосредственных связей. Для её составления для каждого логического элемента записывается булева функция, то есть связь между входом и выходом. Затем производится последняя замена переменных, начиная с элементов последнего ранга и продолжение замены в направлении входных полюсов (**то есть суперпозиция, то есть замена выходных переменных входными).
К схеме:
Y=k*l

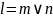

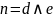
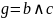
2. ДНФ
В этой модели функция, реализуемая ДУ как булева функция, аргументами которой являются входные переменные.
Y=f (a, b, c, d, e)
Составление её производится по принципу суперпозиции (см. скобку **). При этом аргументом, то есть буквами булевых выражений уравнений непосредственных связей присваиваются индексы логических элементов. Которые выполняют данную логику.
Y=k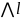
Заменяем «k» и «l»

Каждый элемент расписываем:


Индексы означают, какой элемент выполняет данную операцию.
Примечание:
Выражение, где присутствуют индексы элементов, называются эквивалентной нормальной формой (ЭНФ), которая помимо аналитического описания ДУ отражает его структуру, так как присутствуют индексы логических элементов.
3.Покрытие ду
Булевы функции «n» - элементов можно представить в виде отображения на n-мерный куб. Множества кубов, называемое покрытием, соответствует аналитической модели ДУ, представленной в виде ДНФ.
Куб – это: Строки
«1»
покрытие «0»
покрытие
куб
1
куб 2
куб 3


1 |
2 |
3 |
1 |
Х |
1 |
Х |
1 |
1 |
0 |
0 |
0 |
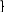 2
2
1,2,3 – вершины куба.
Разделимые арифметические коды.
Для кодирования двоичного слова необходимо использовать вычисление остатков по двум модулям. При этом комбинации весовых коэффициентов не повторяются.
q1=5 ИР КР
|
|
… |
ra1 |
ra2 |
Разделимые арифметические коды позволяют обнаружить разряд, в котором произошло искажение и скорректировать ошибку этого разряда (однократную ошибку).
Весовые коэффициенты:
q=5

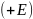 – положительная
ошибка;
– положительная
ошибка;

 -
отрицательная
ошибка;
-
отрицательная
ошибка;
q=7

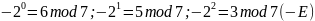

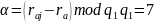

 -
остаток искажённого символа;
-
остаток искажённого символа;
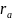 -
остаток
неискажённого слова;
-
остаток
неискажённого слова;
 для
положительной ошибки
для
положительной ошибки
 для отрицательной ошибки
для отрицательной ошибки
α |
4 |
3 |
2 |
1 |
6 |
0 |
9 |
6 |
3 |
5 |
4 |
1 |
10 |
7 |
3 |
8 |
5 |
2 |
11 |
β α |
1 |
2 |
4 |
3 |
1 |
0 |
9 |
6 |
3 |
2 |
4 |
1 |
10 |
7 |
4 |
8 |
5 |
2 |
11 |
Свёртка
числа по модулю q определяется как
разность
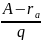
На основании приведённых значений свёрток и при использовании формул вычисляются коэффициенты α и β.
И в соответствии с вычисленными значениями составляется таблица для определения искажённого разряда, в котором возникает положительная ошибка.
Для модуля q=7:
A=12


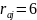
По модулю 5:
A=12
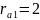
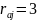
Вычисляем коэффициенты:
α=1 β=1
Если α=β=0, то искажений в слове нет. Иначе используется таблица для коррекции искажений.
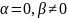 – искажения
в КР по модулю q.
– искажения
в КР по модулю q.
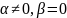 – искажения
в КР по модулю q.
– искажения
в КР по модулю q.

 β
β