37. Необходимое и достаточное условие дифференцируемости. Дифференцируемость и непрерывность.
Необходимое
условие:
Достаточное
условие:
Дифференцируемость и непрерывность:
из непрерывности функции не следует ее дифференцируемость.
из дифференцируемости функции следует ее непрерывность.
Рассмотрим
более конкретно каждый вопрос. Чтобы
ответить на данные вопросы необходимо
доказать озвученый факт или привести
пример, который опровергает этот факт.
Найдем
производную следующей функции
.
Хорошо известно, данная функция является
непрерывной и, что ее производная будет
следующей:
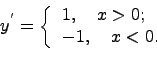
Покажем, что в точке нуль производная не существут. Для этого найдем производную в нуле по определению производной:
данный
предел равен 1, если
и
равен (-1), если
,
получаем, что предел не существует,
следовательно в нуле производной нет
и функция в нуле не дифференцируема.
38. Правила вычисления производных.
Если
функции f и g имеют конечные
производные при
,
то:
1)
-
постоянные;
2)
;
3)
.
39.
Производные элементарных функций.
40. Производная сложной функции, производная обратной функции. Примеры.
Производная композиции (сложной функции)
Производная
обратной функции
Логарифмическая
производная функции f
41. Применение дифференциала для приближенных вычислений значений функции.
Пример 1. Дана функция z = x2 + y2 – 2·x + 2·y и две точки А(1, 2) и В( 1,08; 1,94 ). Найти:
значение функции в точке В;
приближённое значение z1 функции в точке В, заменяя приращение функции при переходе от точки А к точке В дифференциалом; оценить в процентах относительную погрешность вычисления при замене приращения функции дифференциалом.
Решение. Вычислим значение функции в точке В:
z(B) = 1,08² + 1,94² – 2·1,08 + 2·1,94 = 6,65.
Приближенное значение z1 в точке В найдём по формуле линеаризации:
z1(B) = z0 + dz, где z0 = z(1, 2) = 12 + 22 – 2·1 + 2·2 = 7.
Найдём приращения аргументов
Δ x = x – x0 = 1,08 – 1 = 0,08; Δ y = y – y0 = 1,94 - 2 = - 0,06.
Найдём значения частных производных функции в точке А
.
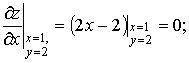
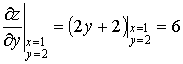Найдём значение дифференциала
Приближённое значение функции в точке В равно z = 7 − 0,36 = 6,64. Относительная погрешность вычисления равна
Пример
2.
Гипотенуза с
и катет а
определяются с максимальными абсолютными
погрешностями | Δ с
| =0,2; |Δ а|
= 0,4 и соответственно равны с
= 75, а
= 32. Определить угол А по формуле
и
максимальную абсолютную погрешность
|Δ А| измерения этого угла.
Решение.
Из условия примера имеем
.
Вычислим частные производные
.
Заменяя приращение величины её дифференциалом, получим
.
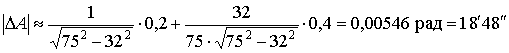Таким образом,
.
42. Производные и дифференциалы высших порядков. Примеры.
Производные высших порядков Рассмотрим функцию y=f(x), определенную на некотором промежутке (a,b) . Вычислим производную y', которая также является функцией на (a,b). Производной второго порядка от функции y=f(x) называется производная от ее производной:y''=(y')' . Аналогично определяют производную любого порядка: y(n)=(y(n-1))' .
Дифференциалы высших порядков: Рассмотрим дифференциал функции y=f(x) в произвольной точке промежутка (a,b): dy=f'(x)dx. Здесь dx - приращение независимой переменной, которое является числом и не зависит от x. Сам же дифференциал есть функция от x, и можно вычислить дифференциал от этой функции: d(dy)=(f'(x)dx)'dx1 При dx=dx1 этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле d2y=f''(x)dx2 Аналогично вычисляется дифференциал любого порядка dny=f(n)(x)dxn .
Производные n-го порядка от основных элементарных функций
43. Необходимое условие экстремума дифференцируемой. Теорема Ферма. функции в точке x0 функция достигает экстремума, если для любых x из некоторой окрестности точки x0 выполняется неравенство f (x) ≤ f (x0) (минимум) или f (x) ≥ f (x0) (максимум). Необходимое условие экстремума. Во всех точках экстремума производная функции не существует или равна нулю. Теорема Ферма. Если функция f (x) дифференцируема в точке x0 и достигает в ней экстремума, то
|
График .Теорема Ферма: касательная к графику функции в точке экстремума параллельна оси абсцисс