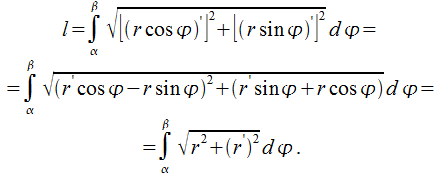11. Вычисление двойного интеграла в полярных координатах. Замена переменных в двойном интеграле.

Вычисление двойного интеграла в полярных координатах.

Если D^* – область в полярной системе, соответствующая области D в прямоугольной системе, то

 

 

Замена переменных в двойном интеграле. Пусть функции  взаимно однозначно отображают открытое множество, содержащее область  плоскости  на открытое множество, содержащее область  , и пусть  является образом  . Если  и их частные производные непрерывны, а определитель    , то  . Выражение   называется элементом площади в криволинейных координатах, функциональный определитель  - якобианом.

12. Замена переменных в тройном интеграле. Цилиндрические координаты . Сферические координаты.

Замена переменных в тройном интеграле  состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам

Если выполняются условия

1?. Отображение (6) взаимно однозначно;

2?. Функции в (6) непрерывно - дифференцируемы в области 

3?. Якобиан отображения

то имеет место формула

Формулы (6) называют криволинейными координатами (u, v, w) в области T

 Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).

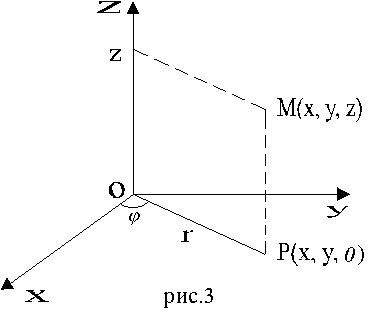
Пусть M(x, y, z) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел  - полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид

Якобиан отображения (8) 

Сферические координаты. Пусть M(x, y) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел  , где r - расстояние точки M до точки 0,  - угол между лучами OM и OZ,  - полярный угол точки P на плоскости xy. Тройка чисел  называется сферическими координатами точки M.

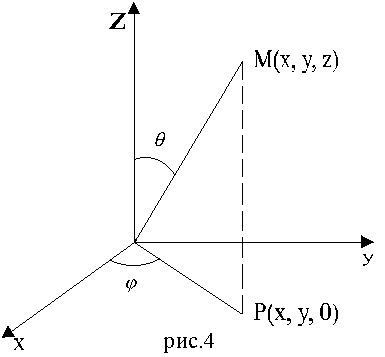
Они связаны с прямоугольными формулами

Якобиан отображения  . Иногда используются обобщённые сферические координаты.

Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой

Переходя в этом равенстве к новым переменным по формулам (6), получим выражение объёма области T в криволинейных координатах

Пусть T - материальное тело (кубируемая область) с плотностью 

Тогда

- масса тела.

13. Криволинейный интеграл 1 рода.

Криволинейным интегралом первого типа от функции f(х, у) по кривой L называется предел интегральной суммы (1.1) при и max : (4.2)

 Криволинейный интеграл 1-го рода (Кри-1)      Сведение Кри-1 к определенному интегралу

     Если кривая l задана уравнением то

     Если кривая l задана параметрически то

Свойства.

1. По самому определению криволинейный интеграл первого типа не зависит от направления пути интегрирования:

;

2) ;

3) (c=const);

4) если путь интегрирования L разбит на части L₁, L₂, ... , L_n, то

.

Криволинейный интеграл 2 рода.

Криволинейным интегралом второго рода или криволинейным интегралом по координатам Называется предел интегральной суммы (21.8) при

 Криволинейный интеграл 2-го рода (Кри-2)      Изменение направления обхода по кривой

     Сведение Кри-2 к определенному интегралу

     1. Кривая l задана уравнением y = f(x), x изменяется от до :

     2. Кривая l задана параметрически: x = x(t), y = y(t), t изменяется от до :

     Сведение Кри-2 к Кри-1

где - угол между направлением касательной к кривой l, согласованным с направлением обхода на кривой, и положительным направлением оси Ох.

Свойства.

1.

2.

3.

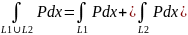
4.

Длина дуги кривой.

Длина дуги кривой в параметрической форме

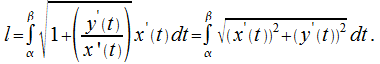
Длина дуги в полярных координатах