Контрольная работа № 1 по математике предисловие

Контрольная работа содержит задания из трех разделов математики: математическому анализу, линейной алгебре и аналитической геометрии.

Каждая контрольная работа должна быть сделана в отдельной тетради, на обложке которой студенту следует разборчиво написать свою фамилию, инициалы, шифр, номер контрольной работы, название дисциплины.

Решения задач необходимо проводить в той же последовательности, что и в условиях задач. При этом условие задачи должно быть полностью переписано перед ее решением.

Студент выполняет тот вариант контрольной работы, последняя цифра которого совпадает с последней цифрой его учебного шифра в зачетной книжке.

Контрольные задания по математическому анализу рекомендуемая литература

1. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. / В.А. Кудрявцев, Б.П. Демидович. М. : Наука, 1989. 656 с.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления. в 2 т. М. : Наука, 1968. Т 1. 551 с.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления. в 2 т. М. : Наука, 1968. Т 2. 312 с.

4. Шипачев В.С. Высшая математика. М. : Высш. шк., 1996. 480 с.

5. Сборник индивидуальных заданий по высшей математики : в 3ч. / А.П. Рябушко, В.В. Бархатов, В.В. Державец, И.Е. Юруть.. Минск : Высшэйш. шк., 1990. Ч. 1. 270 с.

Контрольная работа № 1 по математическому анализу.

Введение в анализ. Дифференциальное исчисление функции одной и двух переменных.

Основные теоретические сведения и методические указания

I. ПРЕДЕЛЫ

1. Множество вещественных чисел. Числовые последовательности. Предел. Верхние и нижние пределы множеств. Существование предела монотонной ограниченной последовательности. Число е. Натуральные логарифмы.

2. Понятие предела функции в точке. Понятие функции, ограниченной в окрестности точки. Теорема об ограниченности функции, имеющей предел.

3. Теорема о переходе к пределу в неравенствах.

4. Теорема о пределе промежуточной функции.

5. Понятие непрерывности функции. Первый замечательный предел 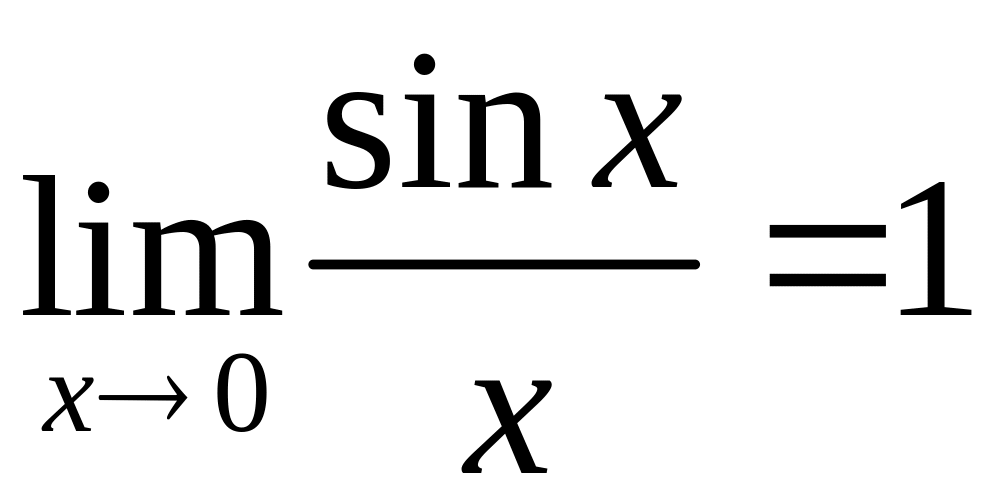. Второй замечательный предел .

6. Понятие бесконечно малой функции. Теорема о связи между функцией, ее пределом и бесконечно малой.

7. Теорема о сумме бесконечно малых функций.

8. Теорема о произведении бесконечно малой функции на ограниченную функцию.

9. Теорема об отношении бесконечно малой функции к функции, имеющей предел, отличный от нуля.

10. Теорема о пределе суммы.

11. Теорема о пределе произведения.

12. Теорема о пределе частного.

13. Теорема о переходе к пределу под знаком непрерывной функции.

14. Непрерывность суммы, произведения и частного.

15. Непрерывность сложной функции.

16. Понятие бесконечно большой функции. Теоремы о связи бесконечно больших функций с бесконечно малыми.

17. Сравнение бесконечно малых функций.

18. Эквивалентные бесконечно малые функции. Теорема о замене бесконечно малых функций эквивалентными.

19. Условие эквивалентности бесконечно малых функций.

II. Дифференцирование

1. Понятие производной. Производная функции .

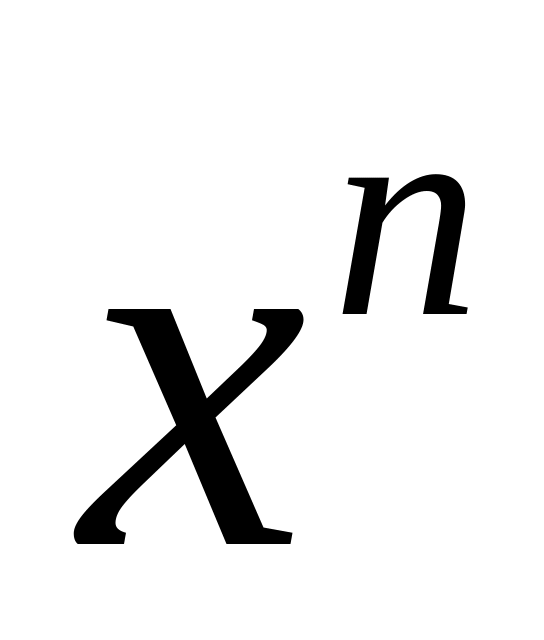2. Геометрический смысл производной. Уравнения касательной и нормали к графику функции.

3. Понятие дифференцируемости функции и дифференциала. Условие дифференцируемости. Связь дифференциала с производной.

4. Геометрический смысл дифференциала.

5. Непрерывность дифференцируемой функции.

6. Дифференцирование постоянной и суммы, произведения и частного.

7. Производная сложной функции.

8. Инвариантность формы дифференциала.

9. Производная обратной функции.

10. Производные обратных тригонометрических функций.

11. Дифференцирование функций, заданных неявно и параметрически.