
- •Расчетно-графическая работа по дисциплине «Методы оптимизации» на тему «Решение задач линейного программирования»
- •Цели и задачи расчетно-графической работы
- •Теоретическая часть
- •Основная и двойственная задачи линейного программирования
- •Транспортная задача
- •Решение задач линейного программирования с помощью пакета Solver
- •Задания Задание 1
- •Задание 2
- •Задание 3
- •Методика выполнения заданий
- •8. Требования к содержанию и оформлению отчета
Расчетно-графическая работа по дисциплине «Методы оптимизации» на тему «Решение задач линейного программирования»
Цели и задачи расчетно-графической работы
Цель работы: приобретение навыков решения задач линейного программирования и транспортных задач с помощью MS Excel.
Задачи работы:
Научиться формулировать математическую постановку основной и двойственной задачи линейного программирования;
Научиться сводить транспортную задачу к задаче линейного программирования;
Научиться искать решение задач линейного программирования с помощью надстройки Solver пакета MS Excel.
Теоретическая часть
Основная и двойственная задачи линейного программирования
В теории линейного программирования в качестве основной можно принять следующую задачу максимизации линейной функции на множестве решений системы линейных уравнений и неравенств.
Задача I. Заданы вещественные числа
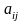 ,
,
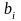 ,
,
 ,
,
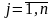 ,
,
и фиксированы разбиения каждого из множеств
 ,
,

на два непересекающихся подмножества
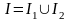 ,
,
 ,
,
 ,
,
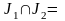 .
.
Требуется максимизировать линейную функцию
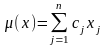 (1)
(1)
на множеств n-мерных векторов
х = (х1, х2, . . ., хn), (2)
удовлетворяющих условиям
 ,
,
 , (3)
, (3)
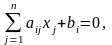
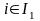 , (4)
, (4)
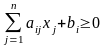 ,
,
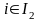 . (5)
. (5)
Вектор (1), удовлетворяющий условиям (3) — (5), называется допустимым, а искомый допустимый вектор, доставляющий максимум функции (1), — оптимальным. Сразу же отметим, что в поставленной задаче не при любых исходных данных имеются допустимые векторы, так как условия (3) — (5) могут оказаться несовместными. Далее, при наличии допустимых векторов не обязательно существуют оптимальные. Соответствующие примеры читателю предлагается построить самостоятельно.
Решающим в исследовании задачи I является рассмотрение наряду с пей еще одной экстремальной задачи, которая тесно связана с первой и является в определенном смысле двойственной к ней.
Задача I*. При исходных данных задачи I минимизировать линейную функцию
 (6)
(6)
на множестве m-мерных векторов
y = (y1, y2, ..., yn), (7)
удовлетворяющих условиям
 ,
, (8)
,
, (8)
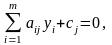
 , (9)
, (9)
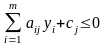 ,
. (10)
,
. (10)
Аналогично предыдущему вектор (7), удовлетворяющий условиям (8) – (10), называется здесь допустимым, а искомый допустимый вектор, доставляющий минимум функции (6) – оптимальным.
Отметим, что и в этой задаче не обязательно имеются допустимые векторы, а при наличии допустимых векторов не всегда существуют оптимальные.
Задачу I называется основной, а отвечающая ей задача I* — двойственной.
Легко
видеть, что каждому ограничению
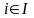 основной задачи отвечает в двойственной
задаче переменная
основной задачи отвечает в двойственной
задаче переменная
 с тем же номером
,
а каждой переменной
с тем же номером
,
а каждой переменной
 задачи I — ограничение
задачи I* с тем же номером
задачи I — ограничение
задачи I* с тем же номером
 .
При этом на переменную
накладывается ограничение неотрицательности,
если
,
т. е. эта переменная отвечает ограничению
в форме неравенства. Аналогично в
двойственной задаче в форме неравенств
задаются ограничения с номерами
,
т. е. отвечающие неотрицательным
переменным
,
задачи I. Далее, в каждом
ограничении
двойственной задачи коэффициент при
переменной
совпадает с коэффициентом при
переменной
в соответствующем ограничении
основной задачи. Что касается свободных
членов в ограничениях (9) и (10), то они
совпадают с коэффициентами при
соответствующих переменных в линейной
функции (1). Наконец, коэффициенты при
переменных в линейной функции (6)
совпадают со свободными членами в
соответствующих ограничениях (4) и (5).
Сказанное позволяет без излишней
формализации по любой конкретной задаче
I записать отвечающую ей
задачу I*.
.
При этом на переменную
накладывается ограничение неотрицательности,
если
,
т. е. эта переменная отвечает ограничению
в форме неравенства. Аналогично в
двойственной задаче в форме неравенств
задаются ограничения с номерами
,
т. е. отвечающие неотрицательным
переменным
,
задачи I. Далее, в каждом
ограничении
двойственной задачи коэффициент при
переменной
совпадает с коэффициентом при
переменной
в соответствующем ограничении
основной задачи. Что касается свободных
членов в ограничениях (9) и (10), то они
совпадают с коэффициентами при
соответствующих переменных в линейной
функции (1). Наконец, коэффициенты при
переменных в линейной функции (6)
совпадают со свободными членами в
соответствующих ограничениях (4) и (5).
Сказанное позволяет без излишней
формализации по любой конкретной задаче
I записать отвечающую ей
задачу I*.
