Билет 1.

Векторная величина (вектор) – это физическая величина, которая имеет две характеристики – модуль и направление в пространстве.

Единичный вектор (орт) - называется вектор, длина которого равна единице.

Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Билет 2.

Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: с_i = a_i + b_i

Вычитание векторов (разность векторов) a - b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: с_i = a_i - b_i

Геометрическая интерпретация.

Произведение ненулевого вектора на число - это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация.

Произведение ненулевого вектора на число - это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами.

Условия коллинеарности векторов:

1. Два вектора a и b коллинеарны, если существует число n такое, что a = n · b

2. Два вектора коллинеарны, если отношения их координат равны.

3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.

Билет 3.

Линейной комбинацией векторов a₁, ..., a_n с коэффициентами x₁, ..., x_n называется вектор x₁a₁ + ... + x_na_n.

Линейная комбинация x₁a₁ + ... + x_na_n называется тривиальной, если все коэффициенты x₁, ..., x_n равны нулю.

Линейная комбинация x₁a₁ + ... + x_na_n называется нетривиальной, если хотябы один из коэффициентов x₁, ..., x_n не равен нулю.

Вектора a₁, ..., a_n называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору.

Вектора a₁, ..., a_n называются линейно зависимыми, если существует нетривиальная комбинация этих векторов равная нулевому вектору.

Свойства линейно зависимых векторов:

1. Коллинеарные вектора - линейно зависимы.

2. Три компланарные вектора - линейно зависимы.

3. n + 1 вектор всегда линейно зависимы.

Базисом на плоскости называются два любых линейно независимых вектора.

Базисом в пространстве называются три любых линейно независимых вектора.

Декартовой прямоугольной системой координат на плоскости (в пространстве) называют две (три) взаимно перпендикулярные оси с общим началом. Первая ось OX называется осью абсцисс, вторая ось OY - осью ординат (третья ось OZ - осью аппликат).

Каждой точке плоскости (пространства) ставится в соответствие упорядоченная пара (тройка) действительных чисел - координат данной точки.

Билет 4.

Проекцией вектора AB на ось l называется число, равное величине отрезка A_lB_l оси l, где точки A_l и B_l являются проекциями точек A и B на ось l.

Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки. Компонента – проекция вектора на оси.

Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

Билет 5.

Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними: a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Свойства скалярного произведения векторов:

1. Скалярное произведение вектора самого на себя всегда больше или равно нуля: a · a ≥ 0

2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору: a · a = 0 <=> a = 0

3. Скалярное произведение вектора самого на себя равно квадрату его модуля:

a · a = |a|2

4. Операция скалярного умножения коммуникативна:

a • b = b • a

5. Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:

a ≠ 0, b ≠ 0, a • b = 0 <=> a ┴ b

6. (αa) • b = α(a • b)

7. Операция скалярного умножения дистрибутивна:

(a + b) · c = a · c + b · c

Ортогональные вектора – перпендикулярные вектора.

Билет 6.

Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма, построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора с.

Свойства векторного произведения векторов:

1. Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах: S_парал = [a × b]

2. Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.

3. Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.

4. a × b = -b × a

5. (k a) × b = a × (k b) = k (a × b)

6. (a + b) × c = a × c + b × c

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами.

Билет 7.

Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.

Свойства смешанного произведения векторов:

1. Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами: V_парал = a · [b × c]

2. Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.

3. a • [b × c] = b • (a • c) - c • (a • b)

4. a • [b × c] = b • [c × a] = c • [a × b] = = -a • [c × b] = -b • [a × c] = -c • [b × a]

5. a • [b × c] + b • [c × a] + c • [a × b] = 0 - тождество Якоби.

Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.

Билет 8.

Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами.

Элементы матрицы A обозначаются a_ij, где i - номер строки, в которой находится элемент, j - номер столбца.

Строка(столбец) матрицы называется нулевой/ым, если все ее/его элементы равны нулю.

Главной(побочной) диагональю матрицы называется диагональ, проведённая из левого(правого) верхнего угла матрицы в правый(левый) нижний угол.

Следом матрицы называется сумма диагональных элементов матрицы. trA = a₁₁ + a₂₂ + ... + a_nn

Вектор-строкой(столбцом) называется матрица, состоящая из одной строки(столбцом).

Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

Результатом умножения матриц A_m×n и B_n×k будет матрица C_m×k такая, что элемент матрицы C, стоящий в i-той строке и j-том столбце (c_ij), равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:

c_ij = a_i1 · b_1j + a_i2 · b_2j + ... + a_in · b_nj

Билет 9.

Транспонирование матрицы - это операция над матрицей, при которой ее строки и столбцы меняются местами: a^T_ij = a_ji

Свойства транспонированной матрицы:

1. Если матрица A имеет размер n×m, то транспонированная матрица A^T имеет размер m×n

2. (A^T)^T = A;

3. (k • A)^T = k • A^T;

4. (A + B)^T = A^T + B^T;

5. (A • B)^T = B^T • A^T.

Билет 10.

Обратная матрица A^-1 — матрица, произведение которой на исходную матрицу A равно единичной матрице E: A·A^-1 = A^-1·A = E

Свойства обратной матрицы:

1. det(A^-1) = 1/det(A)

2. (A·B)^-1 = A^-1·B^-1

3. (A^-1)^T = (A^T)^-1

4. (kA)^-1 = A^-1/k

5. (A^-1)^-1 = A

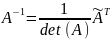
Билет 11.

Действительная квадратная невырожденная матрица A называется ортогональной, если A^-1=A^T.

Свойства ортогональной матрицы:

1. A^TA=E=AA^T

2. |detA|=1 — модуль определителя ортогональной матрицы равен единице.

3. Матрица A^-1 (или, что то же самое A^T) является ортогональной.

4. Произведение ортогональных матриц одного и того же порядка является ортогональной матрицей.

Билет 12.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарными преобразованиями строк называют:

1. перестановку местами любых двух строк матрицы

2. умножение на ненулевую константу любой строки матрицы

3. прибавление к любой строке матрицы другой строки, умноженной на ненулевое число

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.