3.3. Наибольшее и наименьше значение функции в замкнутой области

Поняти наибольшего и наименьшего значения функции многих пере­мен­ных определяется так же, как и для функции одной переменной

Hаибольшим значением f(P) в области D называется число M = f(P0), если P0 ∈ D и для всех Р этой области выполняется неравенство M ≥ f(P).

Hаименьшим значением f(P) в области D называется число m = f(P0), если P0 ∈ D и для всех Р этой области выполняется неравенство m ≤ f (P).

Функция нескольких переменных, дифференцируемая в ограниченной замкнутой области, достигает наибольшего и наименьшего значений или в стационарной точке, или в точках границы области.

Для того чтобы найти наибольшее и наименьшее значения функции в замкнутой области, надо:

1) найти стационарные точки, расположенные в данной области, и вычислить значения функции в этих точках;

2) найти наибольшее и наименьшее значения функции на линиях, образующих границу области;

3) из всех найденных значений выбрать наибольшее и наименьшее.

3.4. Производная по направлению. Градиент

Рассмотрим функцию z = f(M), определенную в некоторой окрестности ^{точки M(x;y), и произвольный единичный вектор}

Проведем в направлении вектора l прямую MM1 . Точка M1 имеет коор­динаты (x + x; y + y). Величина отрезка MM1 равна

Функция f(M) при этом получит

приращение:

z = f(x + x; y + y) - f(x; y)

Предел отношения при

(M M1 ), если он существует и ко­нечен, называеlтся производной функции z = f(M) в точке M(x;y) по направлению вектора l и обозначается , т.е. .

При нахождении производной по направлению пользуются формулой:

⁽¹⁾

Градиентом функции z = f(M) в точке M(x;y) называется вектор, коор­ди­наты которого равны соответствующим частным производным и , взятым в точке M(x; y). Обозначается:

⁽²⁾

Учитывая определение градиента, формулу (1) можно представить в виде скалярного произведения двух векторов:

(3)

Аналогично определяется производная по направлению и градиент функ­ции трех переменных u = f(x; y; z):

.

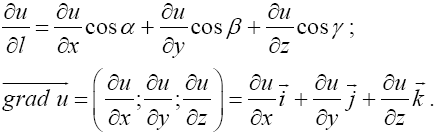
Градиент функции характеризует направление, а его модуль величину наибыстрейшего роста функции в данной точке (наибольшую скорость изме­нения функции в точке). Понятия производной по направлению и градиента функции играют важную роль во многих приложениях.