Дифференциал функции
Пусть
функция
имеет в точке
конечную, не равную нулю производную.
Можно показать, что приращение функции
в окрестности этой точки может быть
представлено в виде суммы двух слагаемых
,
где
– бесконечно малая величина при
.Так
как производная функции равна константе,
то слагаемое
представляет собой бесконечно малую
величину более высокого порядка малости
по сравнению с
и с
(так как является произведением двух
бесконечно малых величин), а первое
слагаемое будет являться главной частью
приращения функции.
Дифференциалом
функции
в точке
называется главная линейная относительно
приращения аргумента
часть приращения функции
и обозначается
.
Формула
вычисления дифференциала имеет вид
Производная высших порядков
1 Повторное дифференцирование функций, заданных в явном виде
Пусть
функция
дифференцируема в некоторой точке.
Тогда
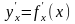есть производная первого порядка этой
функции. Эта производная является
функцией той же независимой переменной,
если эта функция дифференцируема, то
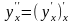– производная второго порядка данной
функции и т.д.
Производная
n-го
порядка есть производная от производной
(n-1)-го
порядка, т.е.
.
Касательная и нормаль к кривой на плоскости
Пусть
дана дифференцируемая функция
и требуется составить уравнение
касательной к графику этой функции в
точке
.
Из геометрического смысла производной
следует, что значение производной в
точке
равно угловому коэффициенту касательной,
проведенной к графику функции в этой
точке, т.е.
,
причем
,
а
– угол наклона касательной с положительным
направлением оси OX.
Для
составления уравнения касательной
воспользуемся уравнением прямой,
проходящей через точку
с заданным угловым коэффициентом k:
,
где
,
.
Т.о.
уравнение
касательной
или
.
(3)
Нормалью к кривой в заданной точке называется прямая, проходящая через точку касания перпендикулярно касательной.
И
з
геометрии известно, что угловые
коэффициенты взаимно перпендикулярных
прямых связаны соотношением:.
Поэтому уравнение нормали имеет вид: или
Правило лопиталя
Производные
можно использовать для вычисления
пределов при раскрытии неопределенностей
вида
и
.Правило
Лопиталя:
Предел отношения двух бесконечно малых или двух бесконечно больших функций равен пределу отношения производных этих функций, если он существует
.
При использовании правила Лопиталя следует обратить внимание на следующее:
1) перед тем, как применять правило Лопиталя, необходимо убедиться в наличии неопределенностей указанных видов;
2) правило говорит о том, что нужно дифференцировать не всю дробь, а отдельно числитель и знаменатель;
3) к правилу Лопиталя имеет смысл обращаться в тех случаях, когда производные числителя и знаменателя находятся не слишком сложно и не приводит к громоздким выражениям;
4) если после однократного использования правила Лопиталя неопределенность сохранилась, то можно применять его повторно до тех пор, пока неопределенность не исчезнет, на каждом этапе проводя упрощение выражений.