2 Простейшие задачи аналитической геометрии

Прежде чем приступить к изучению алгебраических кривых и поверхностей

1–го порядка, рассмотрим некоторые простые, часто встречающиеся задачи.

А) Вычисление расстояния между точками. Пусть в пространстве задана система координат и имеются 2 точки: М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂). Требуется найти расстояние между ними. Ясно, что это расстояние равно длине вектора . Координаты мы умеем вычислять:

= (x₂ – x₁, y₂ – y₁, z₂ – z₁) .

Поэтому его длина .

Аналогично, расстояние между двумя точками М₁(x₁, y₁) и М₂(x₂, y₂) на плоскости равно . Расстояние между точками М₁, М₂ можно обозначать и без черты сверху: |М₁М₂| .

Пример 5. Найти длины сторон треугольника АВС, если его вершины находятся в точках А(3, 0, 2), В(5, –1, 4), С(2, 1, 0).

Решение. .

Аналогично .

Б) Деление отрезка в данном отношении. Пусть даны две точки: М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂). Разделить М₁М₂ в отношении ₁ : ₂ означает: найти на этом отрезке точку М(x, y, z) так, чтобы . Найдём координаты точки М. Для этого рассмотрим векторы

.

Эти векторы коллинеарны, одинаково направлены. Поэтому существует число  > 0 такое, что . Но тогда , поэтому . Получаем: (x – x₁, y – y₁, z – z₁) = (x₂ – x, y₂ – y, z₂ – z).Сравним первые координаты: (x – x₁) = (x₂ – x) . Отсюда найдём x: ₂x – ₂x₁ = ₁x₂ – ₁x, ₂x + ₁x = ₁x₂ + ₂x₁, .

Аналогично .

Очевидно, формулы для плоской задачи такие же.

Пример 6. Найти точку пересечения медиан в треугольнике с вершинами

А(2, –3), В(0, 5), С(4, 1).

B

K D

A

C

Решение. Как известно из школьной геометрии, точка пересечения медиан делит каждую медиану в отношении 2 : 1, считая от вершины. В нашем случае: . Найдем сначала координаты точки D. По определению медианы: . По формулам деления отрезка получаем:

, . Итак, D(2, 3). Опять применяем формулы деления отрезка для отыскания координат точки K :

Ответ: K(2, 1).

В) Пересечение линий. Рассмотрим задачу: найти точки пересечения двух кривых на плоскости. Допустим, что известны уравнения, задающие эти кривые (в некоторой системе координат):

f₁(x, y) = 0 , f₂(x,y) = 0 .

Так как точка пересечения лежит на каждой кривой, то она удовлетворяет каждому уравнению, т.е. удовлетворяет системе уравнений. Обратно, любое решение системы уравнений

определяет координаты точки пересечения кривых.

3 Плоскости в трёхмерном пространстве

Уточним, прежде всего, понятие «плоскость» с помощью определения, хорошо согласованного с нашими интуитивными представлениями.

N

M₀ M

П усть – некоторый ненулевой вектор, M₀(x₀, y₀, z₀) – точка. Плоскостью Р называется множество точек M таких, что векторы и перпендикулярны:

P =  M | перпендикулярен .

Таким образом, чтобы задать плоскость нужна точка M₀ , через которую эта плоскость проходит, и вектор , перпендикулярный к плоскости – он называется вектором нормали.

Теорема 1. Плоскости и только они являются поверхностями 1–го порядка в трёхмерном пространстве.

Доказательство. Пусть P – плоскость, M₀(x₀, y₀, z₀) – точка плоскости,

= (A, B, C) – вектор нормали. Запишем условия того, что некоторая (текущая) точка M(x, y, z) лежит на плоскости:

.

Последнее соотношение (полученное как результат вычисления скалярного произведения в координатной форме) есть уравнение плоскости. Ясно, что это – уравнение первой степени.

Обратно, рассмотрим произвольное уравнение 1–й степени:

Ax + By + Cz + D = 0 .

Здесь хотя бы одно из чисел A, B, C не равно 0 . Возьмем произвольную точку M₀(x₀, y₀, z₀), координаты которой удовлетворяют данному уравнению:

Ax₀ + By₀ + Cz₀ + D = 0.

Вычтем это равенство из общего уравнения:

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0 .

Получили уравнение, равносильное исходному. Но из первой части доказательства видно, что это уравнение задает плоскость, проходящую через M₀(x₀, y₀, z₀) перпендикулярно вектору = (A, B, C). Итак, уравнение Ax + By + Cz + D = 0 задает плоскость. Теорема доказана.

Замечание. Подчеркнём важную роль, которую играет вектор нормали при работе с плоскостью. Если дано уравнение, значит вектор нормали известен. Обратно, если известен вектор нормали, то, зная хотя бы одну точку плоскости, можно написать её уравнение.

Рассмотрим некоторые частные случаи уравнения плоскости. Если D = 0, то точка O(0, 0, 0) удовлетворяет уравнению. Значит плоскость Ax + By + Cz = 0 проходит через начало координат.

Если A = B = 0, т.е. уравнение имеет вид Cz + D = 0 , или , то вектор нормали коллинеарен вектору k = (0, 0, 1). Поэтому плоскость перпендикулярна оси OZ , а значит параллельна плоскости XOY . Координатная плоскость XOY имеет уравнение z = 0 .

Аналогично, x = 0 – уравнение координатной плоскости YOZ ; x = a – уравнение плоскости, параллельной YOZ ; y = 0 – уравнение плоскости XOZ ; y = b – уравнение плоскости, параллельной XOZ.

Если равна нулю только одна из координат вектора нормали, то нормаль перпендикулярна, а плоскость, следовательно, параллельна соответствующей оси. Например, плоскость Ax + Cz + D = 0 параллельна оси OY (возможно, содержит эту ось).

Вопросы о взаимном расположении плоскостей решаются с помощью вектора нормали. Пусть две плоскости заданы своими уравнениями:

A₁x + B₁y + C₁z + D₁ = 0 (плоскость Р₁),

A₂x + B₂y + C₂z + D₂ = 0 (плоскость Р₂).

Запишем в краткой, символической форме условия параллельности и перпендикулярности плоскостей:

Угол между плоскостями равен углу между векторами нормали и находится с помощью скалярного произведения

Как известно, через любые 3 точки, не лежащие на одной прямой, можно провести единственную плоскость. Научимся решать эту важную задачу в общем виде, а затем рассмотрим пример. Пусть точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) не лежат на одной прямой.

Мы помним, что главное для записи уравнения плоскости – найти вектор нормали, т.е. какой–нибудь вектор, перпендикулярный плоскости. В качестве такого вектора можно взять векторное произведение:

,

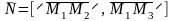так как векторное произведение, по определению, перпендикулярно каждому из сомножителей (см. раздел 4.3). Вычисляя координаты , получим

В качестве точки плоскости для записи уравнения можно взять любую из точек M₁, M₂, M₃. Возьмём, например, M₁ :

.

Левую часть равенства можно записать как определитель 3–го порядка. Получаем уравнение в виде:

.

Приведём другой способ вывода уравнения плоскости, проходящей через 3 данные точки. Пусть M(x, y, z) – произвольная (текущая) точка. Очевидно, M лежит на плоскости тогда и только тогда, когда векторы компланарны.

Условие компланарности векторов записывается с помощью смешанного произведения (см. 4.4):

( ) = 0 .

Или, в координатной форме:

.

Заметим, что получено то же самое уравнение, так как перестановка строк, как мы знаем, может лишь изменить знак определителя. Но если определитель равен 0, то он не меняется.

Решим еще одну задачу о плоскости. Найдём расстояние от точки

M₀(x₀, y₀, z₀) до плоскости Ax + By + Cz + D = 0.

Обозначим через M₁(x₁, y₁, z₁) – основание перпендикуляра, опущенного из M₀ на плоскость. Тогда вектор , очевидно, коллинеарен вектору нормали = (A, B, C). Вычислим их скалярное произведение: (так как косинус угла равен 1, в зависимости от совпадения или несовпадения направлений векторов). С другой стороны, в координатной форме:

.Так как точка M₁(x₁, y₁, z₁) лежит на плоскости, то Ax₁ + By₁ + Cz₁ + D = 0 и, раскрывая скобки, получаем:

Ax₀ + By₀ + Cz₀ + D .

Сравнивая два полученных выражения для , находим расстояние d от точки до плоскости:

.

Знак  мы заменили абсолютной величиной, поскольку расстояние – величина всегда положительная.