Аналитическая геометрия

Аналитическая геометрия как наука, как новый раздел математики, появилась в 1637 году, когда французский философ и математик Рене Декарт опубликовал свой труд “Геометрия”. В основе этой науки лежат идеи использования координатного метода и понятия уравнения линии или поверхности. Оказалось, что многие геометрические задачи можно перевести на алгебраический язык и решать методами алгебры.

.1 Координатный метод. Уравнения линий и поверхностей

Y

N

q

O

p X

Z

c

M

O b

a Y

X

Идея координатного метода состоит в том, чтобы указывать положение точки на плоскости или в пространстве с помощью чисел. Наиболее простой и удобной является декартова прямоугольная система координат. В разделе 4.1 мы уже начали работать с такими координатами. Напомним, что положение точки на плоскости задается двумя числами – абсциссой и ординатой, положение точки в пространстве – тремя числами – абсциссой, ординатой и аппликатой.

Здесь точка М имеет абсциссу а, ординату b, аппликату с (обозначение: M(a, b, c)). Точка N(p, q) имеет абсциссу p, ординату q. Координатные оси являются числовыми прямыми, начало координат О – нулевая точка на каждой из них. Заметим, что абсцисса p точки N отрицательна. Отрицательные части осей OX, OY, OZ в пространстве не изображены на рисунке, однако они существуют – любая из координат может быть как положительной, так и отрицательной.

Кроме декартовой прямоугольной используются и другие системы координат. Одной из них посвящён раздел 5.6 этого модуля.

Развитие координатного метода приводит к важнейшему понятию уравнения

(линии или поверхности). Пусть на плоскости выбрана система координат. Равенство , содержащее переменные x, y , называется уравнением линии L на плоскости, если координаты любой точки линии удовлетворяют этому равенству и, наоборот, любая точка, координаты которой удовлетворяют равенству, лежит на линии L. Другими словами

F(x, y) = 0  M(x, y)  L .

Аналогично вводится понятие уравнения поверхности в пространстве. Пусть в пространстве задана система координат OXYZ. Слова: « Равенство F(x, y, z) = 0 является уравнением поверхности Р » означают, что для любых чисел x, y, z

F(x, y, z) = 0 тогда и только тогда, когда точка М(x, y, z) лежит на поверхности Р.

Y X

O

Y

O

X

Пример 1. Рассмотрим прямую линию на плоскости, делящую угол между осями OX и OY пополам. Её уравнение в системе координат ХOY имеет вид: x – y = 0 (или x = y). Действительно, на этой прямой лежат те и только те точки, координаты которых равны. Заметим, что в какой–либо другой системе координат (например на рисунке) та же самая линия будет иметь другое уравнение.

Пример 2. Уравнение сферы, центр которой совпадает с началом координат и радиус равен 1, имеет вид: x² + y² + z² = 1 .

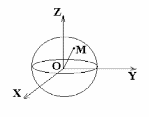
Действительно, точка М(x, y, z) лежит на сфере тогда и только тогда, когда длина вектора равна 1. Как мы знаем, координаты точки М и координаты вектора совпадают. Поэтому . Итак,

М(x, y, z) лежит на сфере 

.

Обычно полученное уравнение заменяют равносильным ему, возводя в квадрат: x² + y² + z² = 1.

Из множества всех линий и поверхностей выделим так называемые алгебраические линии и поверхности. Сначала дадим определение алгебраического уравнения. Алгебраическим уравнением от переменных x, y называется уравнение вида

,

где a_i – действительные числа, показатели степени k_i, l_i – неотрицательные целые числа. Максимальное значение суммы k_i + l_i называется степенью уравнения. Кривая на плоскости, которая в некоторой декартовой системе координат задаётся алгебраическим уравнением n–й степени, называется алгебраической кривой n–го порядка.

В точности так же определяются алгебраические уравнения от 3–х переменных, задающие алгебраические поверхности. Замечание. При изменении декартовой прямоугольной системы координат (сдвиг начала координат, поворот осей) уравнение алгебраической линии (или поверхности) конечно, изменится, но останется алгебраическим, причём той же самой степени. Оставим пока это замечание без подробных пояснений.

Пример 3. 1) x² + y² + z² = 1 – алгебраическое уравнение 2–й степени; значит сфера – алгебраическая поверхность 2–го порядка;

2) x – y = 0 – алгебраическое уравнение 1–й степени;

3) 3x²y + 2xy + 3x – 5 = 0 – алгебраическое уравнение 3–й степени;

4) x² + 3xyz + z² – 1 = 0 – алгебраическое уравнение 3–й степени;

5) y – sinx = 0 – уравнение не является алгебраическим (синусоида не является алгебраической кривой).

В этом модуле будут изучены алгебраические кривые и поверхности 1–го порядка. Кривые и поверхности второго порядка рассмотрим позднее.

Иногда бывает удобно для задания кривой выражать координаты её точек через вспомогательную переменную, так называемый параметр:

x=(t) , y=(t) , t,  .

Каждому значению t,  соответствует точка плоскости с координатами ((t) , (t)) . Можно представлять себе кривую как траекторию движения точки, рассматривая параметр t как время.

Особенно полезен параметрический способ задания для кривых в трёхмерном пространстве. Здесь кривую, вообще говоря, нельзя задать одним уравнением. Если кривая есть пересечение двух поверхностей, то её можно задать системой уравнений:

где уравнения F₁(x, y, z) = 0 , F₂(x, y, z) = 0 задают поверхности, пересекающиеся по данной кривой. Однако параметрический способ во многих случаях удобнее.

Пример 4. Параметрические уравненияx = Rcost , y = Rsint , t0, 2

задают окружность радиуса R с центром в точке O(0, 0). Можно исключить параметр, возведя оба уравнения в квадрат и затем сложив их. Получим x² + y² = 1 – алгебраическое уравнение, определяющее окружность.

Примером пространственной кривой, заданной параметрически, может служить винтовая линия : x = acost , y = asint , z = bt . Если параметр t рассматривать как время, то точка, координаты которой меняются по указанному закону, будет двигаться по цилиндру радиуса a, «наматывая» на его поверхность винтовую линию.