Системы линейных уравнений

М ногие практические задачи сводятся к решению систем алгебраических уравнений 1–й степени или, как их обычно называют, систем линейных уравнений. Мы научимся решать любые такие системы, не требуя даже, чтобы число уравнений совпадало с числом неизвестных.

В общем виде система линейных уравнений записывается так:

.Здесь числа a_ij – коэффициенты системы, b_i – свободные члены, x_i– символы неизвестных. Очень удобно ввести матричные обозначения: – основная матрица системы, – матрица–столбец свободных членов, – матрица–столбец неизвестных. Тогда систему можно записать так: AX=B или, подробнее:

.

Если в левой части этого равенства выполнить умножение матриц по обычным правилам и приравнять элементы полученного столбца к элементам В, то мы придём к первоначальной записи системы.

Пример 14. Запишем одну и ту же систему линейных уравнений двумя разными способами:

Система линейных уравнений называется совместной, если у неё есть хотя бы одно решение, и несовместной, если решений нет.

В нашем примере система совместна, столбик является её решением:

Это решение можно записать и без матриц: x=2, y=1. Систему уравнений будем называть неопределённой, если она имеет более одного решения, и определённой, если решение единственно.

Пример 15. Система является неопределенной. Например являются ее решениями. Читатель может найти и много других решений этой системы.

Научимся решать системы линейных уравнений сначала в частном случае. Систему уравнений АХ=В будем называть крамеровской, если её основная матрица А – квадратная и невырожденная. Другими словами, в крамеровской системе число неизвестных совпадает с числом уравнений и .

Теорема 6. (Правило Крамера). Крамеровская система линейных уравнений имеет единственное решение, задаваемое формулами:

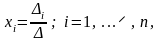
где – определитель основной матрицы, – определитель, полученный из  заменой i–го столбика столбиком свободных членов.

Замечание. Крамеровские системы можно решать и по–другому, с помощью обратной матрицы. Запишем такую систему в матричном виде: AX=В. Так как , то существует обратная матрица А^–1. Умножаем матричное равенство на А^–1 слева: А^–1АХ=А^–1В. Так как А^–1АХ=ЕХ=Х , то решение системы найдено: Х = А^–1В.Такой способ решения будем называть матричным. Ещё раз подчеркнём, что он годится только для крамеровских систем – в других случаях обратная матрица не существует. Разобранные примеры применения матричного метода и метода Крамера читатель найдёт ниже.

Изучим, наконец, общий случай – систему m линейных уравнений с n неизвестными. Для её решения применяется метод Гаусса, который мы рассмотрим подробно.Для произвольной системы уравнений АХ=В выпишем расширенную матрицу. Так называется матрица, которая получится, если к основной матрице А справа дописать столбец свободных членов В:

.

Как и при вычислении ранга, с помощью элементарных преобразований строк и перестановок столбцов будем приводить нашу матрицу к трапецевидной форме. При этом, конечно, соответствующая матрице система уравнений изменится, но будет равносильна исходной (т.е. будет иметь те же решения). В самом деле, перестановка или сложение уравнений не изменят решений. Перестановка столбцов – тоже: уравнения x₁+3x₂+7x₃=4 и x₁+7x₃+3x₂=4, конечно, равносильны. Нужно только записывать, какой неизвестной соответствует данный столбец. Столбец свободных членов не переставляем – его обычно в матрице отделяют от других пунктиром. Возникающие в матрице нулевые строки можно не писать.

Пример 1. Решить систему уравнений:

Решение. Выпишем расширенную матрицу и приведем её к трапецевидной форме. Знак ~ теперь будет означать не только совпадение рангов, но и равносильность соответствующих систем уравнений.

~ . Поясним выполненные действия.

Действие 1. Ко 2–й строке прибавили 1–ю, умножив ее на (–2). К 3–й и 4–й строкам прибавили 1–ю, умножив ее на (–3). Цель этих операций – получить нули в первом столбике, ниже главной диагонали.

Действие 2. Так как на диагональном месте (2,2) оказался 0, пришлось переставить 2–й и 3–й столбики. Чтобы запомнить эту перестановку, написали сверху обозначения неизвестных.

Действие 3. K 3–й строке прибавили 2–ю, умножив ее на (–2). К 4–й строке прибавили 2–ю. Цель – получить нули во втором столбике, ниже главной диагонали.

Действие 4. Нулевые строчки можно убрать.

Итак, матрица приведена к трапецевидной форме. Ее ранг r=2. Неизвестные х₁, х₃ – базисные; х₂, х₄ – свободные. Придадим свободным неизвестным произвольные значения:

х₂ =  , х₄ = .

Здесь ,  могут быть любыми числами. Теперь из последнего уравнения новой системы

x₃+x₄ = –3

находим х₃ : х₃ = –3–. Поднимаясь вверх, из первого уравнения

х₁+3х₃+2х₂+4х₄ = 5

находим х₁: х₁ = 5–3(–3–)–2–4 = 14–2– .

Записываем общее решение:

x ₁=14–2–, x₂=, x₃=–3–, x₄=.

Можно записывать общее решение в виде матрицы–столбца:

При конкретных значениях  и , можно получать частные решения. Например, при =0, =1 получим: – одно из решений системы.

Замечания. В алгоритме метода Гаусса мы видели (случай 1), что несовместность системы уравнений связана с несовпадением рангов основной и расширенной матриц. Приведём без доказательства следующую важную теорему.

Теорема 7 ( Кронекера – Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы системы.