Дифференциальные уравнения второго порядка, допускающие понижение порядка

В общем случае дифференциальное уравнение второго порядка можно записать в виде

где F − заданная функция указанных аргументов.

Если дифференциальное уравнение можно разрешить относительно второй производной y'', то его можно представить в следующем явном виде:

В частных случаях функция f в правой части может содержать лишь одну или две переменных. Такие неполные уравнения включают в себя 5 различных типов:

С помощью определенных подстановок эти уравнения можно преобразовать в уравнения первого порядка.

В случае произвольных дифференциальных уравнений второго порядка, их порядок можно понизить, если эти уравнения обладают определенной симметрией. Ниже мы обсудим 2 типа таких уравнений (случаи 6 и 7):

• Функция F(x, y, y', y'') является однородной функцией аргументов y, y', y'';

• Функция F(x, y, y', y'') является точной производной функции первого порядка Ф(x, y, y').

Итак, рассмотрим указанные случаи понижения порядка более подробно.

Случай 1. Уравнение вида y''= f (x)

Если дано уравнение y'' = f(x), то его порядок можно понизить введением новой функции p(x), такой, что y' = p(x). В результате мы получим дифференциальное уравнение первого порядка

Решая его, находим функцию p(x). Затем решаем второе уравнение и получаем общее решение исходного уравнения.

Случай 2. Уравнение вида y''= f (y)

Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p(y), полагая y' = p(y). Тогда можно записать: и уравнение принимает вид:

Решая его, находим функцию p(y). Затем находим решение уравнения y' = p(y), то есть функцию y(x).

Случай 3. Уравнение вида y''= f (y' ) Для понижения порядка вводим функцию y' = p(x) и получаем уравнение которое является уравнением первого порядка с разделяющимися переменными p и x. Интегрируя, находим функцию p(x) и затем функцию y(x).

Случай 4. Уравнение вида y''= f (x,y' )

Используем подстановку y' = p(x), где p(x) − новая неизвестная функция, и получаем уравнение первого порядка Интегрируя, определяем функцию p(x). Далее решаем еще одно уравнение 1-го порядка и находим общее решение y(x).

Случай 5. Уравнение вида y''= f (y,y' )

Для решения такого уравнения, также как и в случае 2, вводим новую функцию p(y), полагая y' = p(y). Дифференцирование этого равенства по x приводит к уравнению

В результате наше исходное уравнение записывается в виде уравнения 1-го порядка

Решая его, находим функцию p(y). Затем решаем еще одно уравнение первого порядка и определяем общее решение y(x).

Рассмотренные 5 случаев понижения порядка не являются независимыми. Исходя из структуры уравнений, ясно, что случай 2 следует из случая 5, а случай 3 вытекает из более общего случая 4.

П онятие числового положительного ряда.

В общем виде положительный числовой ряд можно записать так: Здесь:

• – математический значок суммы; – общий член ряда; – переменная-«счётчик». Запись обозначает, что проводится суммирование от 1 до «плюс бесконечности». Суммирование в ряде случаев может начинаться с нуля , с двойки либо с любого натурального числа. В соответствии с переменной-«счётчиком» любой ряд можно расписать развёрнуто: – и так далее, до бесконечности.

Сходимость числовых положительных рядов. Необходимый признак сходимости ряда

При этом возможны два случая исследование ряда на сходимость:

1) Ряд 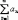расходится. Это значит, что бесконечная сумма равна бесконечности: . Например, Очевидно, что каждый следующий член ряда – больше, чем предыдущий, поэтому и, значит, ряд расходится

2) Ряд сходится. , т.е. бесконечная сумма равна некоторому конечному числу : .

В качестве примера сходящегося числового ряда можно привести бесконечно убывающую геометрическую прогрессию . Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формуле: , где – первый член прогрессии, – основание прогрессии. В данном случае: , . Таким образом: . Получено конечное число, значит, ряд сходится.

Необходимый признак сходимости ряда

Если общий член ряда не стремится к нулю, то ряд расходится. Если , то ряд расходится.

Докажем, что ряд расходится. Общий член ряда : Вывод: ряд расходится, так как не выполнен необходимый признак сходимости ряда.

Признаки сравнения для положительных числовых рядов.

Признак сравнения: Рассмотрим два положительных числовых ряда и . Если известно, что ряд – сходится, и выполнено неравенство (для ), то ряд тоже сходится.

Т.е: Из сходимости ряда с большими членами следует сходимость ряда с меньшими членами.

Признак Даламбера: Рассмотрим положительный числовой ряд . Если существует предел отношения последующего члена к предыдущему: , то:

а) При ряд сходится. В частности, ряд сходится при .

б) При ряд расходится. В частности, ряд расходится при .

в) При признак не дает ответа. Нужно использовать другой признак.

Радикальный признак Коши: Рассмотрим положительный числовой ряд . Если есть предел: , то:

а) При ряд сходится. В частности, ряд сходится при .

б) При ряд расходится. В частности, ряд расходится при .

в) При признак не дает ответа. Нужно использовать другой признак. Признак Коши является более сильным признаком, чем признак Даламбера. Радикальный признак Коши обычно использует в тех случаях, когда общий член ряда ПОЛНОСТЬЮ находится в степени, зависящей от «эн». Либо когда корень извлекается из общего члена ряда. Интегральный признак Коши: Рассмотрим положительный числовой ряд . Данный ряд сходится или расходится вместе с соответствующим несобственным интегралом.

Знакочередующиеся ряды. Признак Лейбница.

Рассмотрим ряд и распишем его подробнее: У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности.

В практических примерах знакочередование членов ряда может обеспечивать не только множитель , но и: , , , …. Например:

Признак Лейбница: Если члены знакочередующегося ряда убывают по модулю, то ряд сходится.

Или, если выполнены оба условия, то ряд сходится:

1) Ряд является знакочередующимся.

2) Члены ряда убывают по модулю. То есть,

Если ряд сходится по признаку Лейбница, то также говорят, что ряд сходится условно. Если сходится и ряд, составленный из модулей: , то говорят, что ряд сходится абсолютно.

Теорема: Если ряд сходится абсолютно, то он сходится и условно.

(Обратное неверно: если ряд сходится условно, то это еще не значит, что он сходится абсолютно.)

Функциональный ряд состоит из ФУНКЦИЙ: Все члены функционального ряда – это функции.

В общий член ряда помимо многочленов, факториалов и др. непременно входит буковка «икс», например:. Разновидностью функционального ряда является степенной ряд.

Степенной ряд – это ряд, в общий член которого входят целые положительные степени независимой переменной . : , где – это «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Например или , где –константа. Например или Область сходимости ряда - это множество значений «икс», при котором степенной ряд будет сходиться.

Для любого степенного ряда возможны три случая:

1. Степенной ряд сходится абсолютно на некотором интервале . Т.е , если мы выбираем любое значение «икс» из интервала и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал и называется интервалом сходимости степенного ряда. Радиус сходимости - половина длины интервала сходимости

2) Степенной ряд сходится абсолютно при любом значении . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают: . Радиус сходимости:

3) Степенной ряд сходится в единственной точке. Если ряд имеет вид , то он будет сходиться в единственной точке . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю: .

Если ряд имеет вид , то он будет сходиться в единственной точке ,

если ряд имеет вид , то, понятно, – в точке «минус а».

Радиус сходимости ряда во всех случаях, естественно, нулевой: .

Поле комплексных чисел

Определения. Пусть a, b – действительные числа, i – некоторый символ. Комплексным числом называется запись вида a+bi .

Сложение и умножение чисел на множестве комплексных чисел: (a+bi)+(c+di) = (a+c)+(b+d)i ,

(a+bi)(c+di) = (ac–bd)+(ad+bc)i. .

Теорема 1. Множество комплексных чисел С с операциями сложения и умножения образует поле. Свойства сложения

1. Коммутативность:(a+bi)+(c+di) = (a+c)+(b+d)i = (c+di)+(a+bi).

2. Ассоциативность :[(a+bi)+(c+di)]+(e+fi) = (a+c+e)+(b+d+f)i = (a+bi)+[(c+di)+(e+fi)].

3. Существование нейтрального элемента:(a+bi)+(0+0i) = (a+bi). Число 0+0i будем называть нулём и обозначать 0.

4. Существование противоположного элемента: (a+bi)+(–a–bi) = 0+0i = 0.

5. Коммутативность умножения: (a+bi)(c+di) = (ac–bd)+(bc+ad)i = (c+di)(a+bi).

6. Ассоциативность умножения:если z₁= a+bi, z₂= c+di, z₃= e+fi, то (z₁z₂)z₃ = z₁(z₂z₃).

7. Дистрибутивность: если z₁= a+bi, z₂= c+di, z₃= e+fi, то z₁(z₂+z₃) = z₁z₂+ z₁z₃.

8. Нейтральный элемент для умножения:(a+bi)(1+0i) = (a·1–b·0)+(a·0+b·1)i = a+bi.

9. Число 1+0i = 1 – единица.

9. Существование обратного элемента:  z  0 z^–1 : zz^–1 = 1.

Пусть z = a+bi. Действительные числа a, называют действительной, а b - мнимой частями комплексного числа z. Используются обозначения: a = Rez, b = Imz.

Если b = 0, то z = a + 0i = a – действительное число. Поэтому множество действительных чисел R является частью множества комплексных чисел C: R  C.

Заметим: i² = (0+1i)(0+1i) = –1+0i = –1. Используя это свойство числа i, а также свойства операций, доказанные в теореме 1, можно выполнять действия с комплексными числами по обычным правилам, заменяя i² на –1.

Замечание. Отношения  ,  («меньше», «больше») для комплексных чисел не определяются.

2 Тригонометрическая форма записи.

Y

в r = a+bi

r 

O a X

Запись z = a+bi называется алгебраической формой записи комплексного числа. Рассмотрим плоскость с выбранной декартовой системой координат. Будем изображать число z точкой с координатами (a, b). Тогда действительные числа a=a+0i будут изображаться точками оси OX – она называется действительной осью. Ось OY называется мнимой осью, её точки соответствуют числам вида bi, которые иногда называют чисто мнимыми. Вся плоскость называется комплексной плоскостью. Число называется модулем числа z: ,

Полярный угол  называется аргументом числа z:  = argz.

Аргумент определяется с точностью до слагаемого 2k; значение, для которого – <   , называется главным значением аргумента. Числа r,  являются полярными координатами точки z. Ясно, что a = r·cos, b = r·sin, и мы получаем: z = a+b·i = r·(cos+i ·sin). тригонометрической форма записи комплексного числа.

Сопряжённые числа. Комплексное число называется сопряжённым числу z = a+bi. Ясно, что . Свойства: .

Замечание. Сумма и произведение сопряжённых чисел есть числа действительные:

, .

Возведение в степень и извлечение корней.

Теорема 2. При умножении комплексных чисел их модули перемножаются, а аргументы складываются.

,

Следствие. Если z = r(cos+i sin), то zⁿ = r ⁿ (cos+i sin).Эта формула Муавра.

Пример 3. Вычислить (i –1)⁶.

Решение. Запишем число –1+ i в тригонометрической форме:

, .

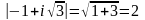Это число изображается точкой во 2–й четверти, поэтому Значит .

Применяем формулу Муавра: .

Научимся теперь извлекать корни, то есть решать уравнения zⁿ = w , где w = |w|(cos+i sin) – данное число, z =|z|(cos+i sin) – неизвестная. Подставим эти выражения в уравнение:

|z|ⁿ(cosn + i sinn) = |w|( cos + i sin).

Отсюда следует, что |z|ⁿ = |w|, n =  + 2k. Выразим теперь искомые величины |z|, :

Окончательно формула для извлечения корней имеет вид:

Здесь – арифметическое значение корня, то есть положительное действительное число. Среди значений различными являются только n, соответствующие значениям k = 0, 1, 2, ... , n–1.

Элементарная теория погрешностей.

Математические действия над приближёнными значениями величин называются приближёнными вычислениями.

Пусть точное значение какой-либо величины равно а её приближённое значение равно Тогда погрешность, т. е. отклонение точного значения от приближённого, равна

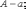
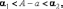она может получиться как положительной, так и отрицательной. Эта погрешность обычно бывает точно неизвестна, поскольку неизвестно значение Поэтому задаются предельные погрешности и между которыми содержится истинная погрешность: т.

В этом случае говорят, что задана двусторонняя оценка величины Так как задавать две предельные погрешности не всегда удобно, то часто задаётся предельная абсолютная погрешность т. е. величина, большая абсолютного значения погрешности: т. е. или

Пусть, к примеру, при измерении некоторой длины получилось ℓ = 137 см, причём можно говорить о точности до см. Это означает, что в данном случае см и см; можно записать см.

П редельная абсолютная погрешность не полностью характеризует точность измерения.. Качество измерения больше характеризуется предельной относительной погрешностью которая вычисляется по формуле

Предельная относительная погрешность безразмерна и часто выражается в процентах, причём для упрощения её значение обычно округляется в сторону увеличения.

Запись приближённых чисел, т. е. приближённых численных значений величин, производится так, чтобы сам вид записи говорил о степени точности. Обычно их записывают так, что все цифры верны, кроме последней, сомнительной, в которой допускается ошибка не больше чем на единицу. К примеру, в равенствах и для сопротивления огромная разница, поскольку эти записи свидетельствуют, что первое вычисление производилось с точностью до а второе − до

Число знаков после запятой говорит о предельной абсолютной погрешности; о предельной же относительной погрешности говорит общее число верных знаков, к которым не относятся передние нули: к примеру, числа 2,57; 1,7100; 0,015; 0,00210 имеют соответственно 3, 5, 2, 3 верных знаков. Чем больше верных знаков в числе, тем меньше предельная относительная погрешность.

Следует избегать записей вида . Если вторая цифра сомнительна, то следует писать а если четвёртая − то

При сложении приближённых чисел в сумме берётся столько знаков после запятой, сколько их имеется у слагаемого с наибольшей абсолютной погрешностью. Если слагаемых много, то ошибки в них могут складываться и дать большую ошибку в сумме. В таких случаях рекомендуется правило лишнего знака: оставлять один лишний знак, а в ответе произвести его округление.

Например, вычислим сумму Самая большая абсолютная погрешность у первого слагаемого: она равна 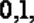поэтому прочие слагаемые округляем до

т. е.

Предельная абсолютная погрешность суммы или разности нескольких величин равна сумме предельных абсолютных погрешностей этих величин.

К примеру, если две величины определены с точностью до то сумма или разность этих величин определены с точностью так как ошибки могут сложиться. Если же слагаемых много, то маловероятно, чтобы все ошибки сложились. В этом случае для определения погрешности суммы следует воспользоваться методами теории вероятностей, из которых вытекает, что один знак в сумме нужно округлять, как это было сделано при вычислении начиная с пяти слагаемых, а два знака − примерно с полутысячи слагаемых.

При вычитании приближённых чисел правила те же, что и при сложении, но необходимо дополнительно иметь в виду, что при вычитании близких чисел относительная точность резко ухудшается.

При умножении или делении двух приближённых чисел следует пользоваться следующим правилом: в ответе число верных знаков надо взять равным наименьшему числу верных знаков в сомножителях или в делимом и делителе.

Важная задача теории погрешностей и метод её решения. Пусть даны приближённые значения и величин с точными значениями и соответственно. Определим, какое из равенств или точнее. Для решения этой задачи существует следующий алгоритм.

1. Найти приближённые значения 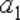и чисел и соответственно с большим числом знаков после запятой, чем у и

2. Найти погрешности вычислений и как разности между двумя приближёнными значениями чисел и соответственно.

3. Определить предельные абсолютные погрешности вычислений и с избытком (округлить полученные значения погрешности вычислений и ).

4. Найти предельные относительные погрешности вычислений по формулам ,

5. Сравнить предельные относительные погрешности вычисления двух чисел, сделать вывод: если равенство точнее равенства если равенство точнее равенства

П ример. Определить, какое равенство точнее:

Решение. Здесь

Воспользуемся алгоритмом решения задачи.

1. Найдём приближённые значения чисел и с большим числом десятичных знаков:

2. Найдём погрешности вычислений и :

3. Определим предельные абсолютные погрешности и с избытком:

4. Найдём предельные относительные погрешности вычислений:

5. Поскольку равенство точнее равенства