3.3 Физический смысл определенного интеграла

П усть материальная точка перемещается под действием силы , направленной вдоль оси и имеющей переменную величину , где – абсцисса движущейся точки .

Р азобьем отрезок произвольным образом на частичных отрезков длиной Так как длина частичного отрезка мала, то силу можно считать на данном отрезке постоянной и равной значению функции в произвольной точке отрезка, . Работа, совершенная этой силой на отрезке , равна . Тогда работа силы на всем отрезке будет приближенно равна

Д анная сумма представляет собой интегральную сумму функции на отрезке , а предел этой суммы при будет равен работе :

Физический смысл определенного интеграла состоит в том, что определенный интеграл численно равен работе силы по перемещению точки вдоль отрезка .

Формула Ньютона-Лейбница Пусть функция интегрируема на , непрерывна на отрезке и – какая-либо ее первообразная на , то .

Пример . Вычислить интеграл .Решение.

3.4 Основные свойства определенного интеграла

1. Определенный интеграл не зависит от обозначения переменной интегрирования: .

2. .

3. Постоянный множитель можно выносить за знак определенного интеграла: , где .

4. , .

5. Если , то .

6. Теорема «о среднем». Если функция непрерывна на , точка такая, что .

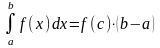Число – среднее значение функции на отрезке .

7. Если функция на отрезке , то на этом отрезке.

8. Е сли на отрезке , то .

9. Если и – соответственно наименьшее и наибольшее значения функции на отрезке , то

10. .

11. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции

3.5 Замена переменной в определенном интеграле Пусть для вычисления интеграла от непрерывной функции на отрезке сделана подстановка .

Теорема . Если:

1. функция и ее производная непрерывны на отрезке ,

2. , ,

3. функция определена и непрерывна на отрезке , то .

Пример . Вычислить интеграл .

Решение. Сделаем тригонометрическую подстановку , тогда .

Найдем пределы интегрирования: если , то , , , если , то , , .

Тогда

3.6 Интегрирование по частям Если функции и имеют непрерывные производные на отрезке , то имеет место формула .

П ример . Вычислить интеграл

Р ешение. интегрирования по частям: , тогда

.Приложения определенного интеграла

1 . Вычисление площади плоской фигуры

И з геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции, ограниченной сверху кривой , снизу отрезком оси ,

справа и слева прямыми и находится по формуле

Е сли криволинейная трапеция расположена ниже оси , то есть то площадь может быть найдена по формуле

П лощадь фигуры, ограниченной кривыми и ( для любого ), прямыми и можно найти по формуле

Е сли криволинейная трапеция ограничена справа непрерывной кривой , слева отрезком оси , снизу и сверху прямыми и , то ее площадь находится по формуле

2. В ычисление объема тела по известным площадям параллельных сечений

Если известны площади сечений тела плоскостями, перпендикулярными оси то объем данного тела находится по формуле

3. Объем тела вращения

4. Пусть вокруг оси вращается криволинейная трапеция, ограниченная линией ( ), отрезком оси и прямыми и Полученная вращением фигура, называется телом вращения.

О бъем тела вращения вокруг оси

находится по формуле или .

Если эту трапецию вращать вокруг оси , то .

5. Вычисление работы переменной силы. Пусть материальная точка перемещается вдоль оси под действием переменной силы , направленной параллельно этой оси. Работа, произведенная силой при перемещении точки из положения в положение , находится по формуле .

6. Путь, пройденный телом Пусть материальная точка перемещается по прямой с переменной скоростью . Тогда путь , пройденный данной точкой за промежуток времени от до , может быть вычислен по формуле .