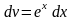- •Курс лекций.
- •1 Матрицы
- •3) Умножение матриц.
- •2 Определители
- •Обратная матрица
- •Ранг матрицы
- •Системы линейных уравнений
- •Аналитическая геометрия
- •.1 Координатный метод. Уравнения линий и поверхностей
- •2 Простейшие задачи аналитической геометрии
- •3 Плоскости в трёхмерном пространстве
- •П редел функции Предел функции в точке о дносторонние пределы
- •Основные теоремы о пределах
- •Непрерывность функции в точке.
- •Теоремы о непрерывности функции
- •Свойства функций, непрерывных на отрезке
- •Понятие производной
- •Основные правила дифференцирования
- •Основные формулы дифференцирования
- •Правило дифференцирования сложных функций..
- •Дифференциал функции
- •Производная высших порядков
- •1 Повторное дифференцирование функций, заданных в явном виде
- •Касательная и нормаль к кривой на плоскости
- •Правило лопиталя
- •Применение производной к исследованию функций
- •Возрастание, убывание функции
- •2 Экстремумы функции
- •3 Наибольшее и наименьшее значения функции на отрезке
- •4 Выпуклость графика функции. Точки перегиба
- •5 Асимптоты графика функции
- •Неопределенный интеграл .1.1 Понятие неопределенного интеграла
- •1.2 Основные свойства неопределенного интеграла
- •2.4 Интегрирование по частям
- •2.5 Интегралы от некоторых функций, содержащих квадратный трехчлен в знаменателе
- •3.2 Геометрический смысл определенного интеграла
- •3.3 Физический смысл определенного интеграла
- •3.4 Основные свойства определенного интеграла
- •О пределение двойного интеграла
- •Г еометрические приложения двойных интегралов
- •2. Объем тела
- •Физические приложения двойных интегралов
- •1. Масса и статические моменты пластины
- •3. Заряд пластины
- •Функция двух переменных
- •Вычислить значение функции z1 в точке в;
- •Вычислить приближенное значение функции в точке в, исходя из ее значения z0 в точке а и заменив приращение функции при переходе от точки а к точке в дифференциалом ;
- •Дифференциальные уравнения. Основные понятия.
- •Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •П онятие числового положительного ряда.
- •Приближенное решение нелинейных алгебраических уравнений
2.4 Интегрирование по частям
Пусть
и
 – дифференцируемые функции. Известно,
что дифференциал произведения
– дифференцируемые функции. Известно,
что дифференциал произведения
 вычисляется по формуле:
вычисляется по формуле:
 .
Проинтегрируем данное равенство
.
Проинтегрируем данное равенство
 .
Используя свойства интеграла, будем
иметь
.
Используя свойства интеграла, будем
иметь
 ,
отсюда
,
отсюда
 .
Данная формула называется формулой
интегрирования по частям.
Эта формула
применяется чаще всего к интегрированию
выражений, которые можно представить
в виде произведения двух сомножителей
.
Данная формула называется формулой
интегрирования по частям.
Эта формула
применяется чаще всего к интегрированию
выражений, которые можно представить
в виде произведения двух сомножителей
 и
и
 ,
причем за
,
принимают такой множитель, от которого
можно найти интеграл.
,
причем за
,
принимают такой множитель, от которого
можно найти интеграл.
Основные
виды интегралов, которые берутся по
частям:
 – многочлен степени
– многочлен степени
 .
.
I |
|
|
|
|
|
||
|
|
||
|
|
||
II |
|
|
|
|
|
||
|
|
||
|
|
||
|
|
||
III |
|
В данных интегралах за можно принять любую функцию. Интегрируют два раза и приводят подобные интегралы. |
|
|
|||
|
|||
|
|||
IV |
|
|
|
|
|
||
П
ример.
Интегрирование
по частям. Найти
интеграл
 .
Решение.
.
Решение.

 тогда
тогда

 ,
,


2.5 Интегралы от некоторых функций, содержащих квадратный трехчлен в знаменателе
К данному методу интегрирования относятся интегралы вида:
1.  ; 2.
; 2.  ;
3.
;
3.  ; 4.
; 4.
 .
.
1.
Рассмотрим интеграл
 .
Преобразуем квадратный трехчлен, выделив
полный квадрат:
.
Преобразуем квадратный трехчлен, выделив
полный квадрат:
 где
где
 .
.
Таким
образом, интеграл
 принимает вид:
принимает вид: .Сделаем
подстановку
.Сделаем
подстановку
 ,
,
 .
Тогда получим
.
Тогда получим
 .
Это уже табличные интегралы (в таблице
19 и 20).
.
Это уже табличные интегралы (в таблице
19 и 20).
П
 ример.
Найти интеграл
ример.
Найти интеграл
 .
Решение.
.
Решение.
 ,
,
 ,
,



 .
.
П онятие
определенного интеграла
онятие
определенного интеграла
Пусть
на отрезке
 задана непрерывная функция
.Разобьем
отрезок
произвольным образом на
частей точками
задана непрерывная функция
.Разобьем
отрезок
произвольным образом на
частей точками
 ,
,
 ,
,
 ,
…,
,
…,
 ,
причем
,
причем
 Длину частичного отрезка разбиения
Длину частичного отрезка разбиения
 обозначим через
обозначим через
 ,
то есть
,
то есть
 .
В каждом частичном отрезке
произвольным образом выберем точку
.
В каждом частичном отрезке
произвольным образом выберем точку
 и найдем значение функции
в каждой точке:
и найдем значение функции
в каждой точке: ,
,
 ,
…,
,
…,
 ,
…,
,
…,
 .
Составим сумму
.
Составим сумму

Данная
сумма называется интегральной
суммой
для функции
на отрезке
.
Пусть
 – длина наибольшего частичного отрезка:
– длина наибольшего частичного отрезка:
 .
Найдем предел интегральной суммы при
.
Найдем предел интегральной суммы при
 :
:
 .
.
Определение
7. Если
интегральная сумма
 имеет предел
имеет предел
 ,
который не зависит ни от способа разбиения
отрезка
на частичные отрезки, ни от выбора точек
в них, то этот предел называют определенным
интегралом от функции
на отрезке
и обозначают
,
который не зависит ни от способа разбиения
отрезка
на частичные отрезки, ни от выбора точек
в них, то этот предел называют определенным
интегралом от функции
на отрезке
и обозначают
 .
Таким
образом,
.
Таким
образом,
 ,
,
где – нижний предел интегрирования,
– нижний предел интегрирования,
 – верхний предел интегрирования,
– подынтегральная функция,
– верхний предел интегрирования,
– подынтегральная функция,
– подынтегральное выражение, – переменная интегрирования, – отрезок интегрирования.
Теорема Коши. Если функция непрерывна на отрезке , то определенный интеграл существует.
3.2 Геометрический смысл определенного интеграла
О пределение
.
Фигура, ограниченная сверху графиком
неотрицательной функции
,
снизу осью
пределение
.
Фигура, ограниченная сверху графиком
неотрицательной функции
,
снизу осью
 ,
справа и слева – прямыми
и
,
справа и слева – прямыми
и
 ,
называется
криволинейной
трапецией.
,
называется
криволинейной
трапецией.
Эта
сумма будет приближенно равна площади
криволинейной трапеции,
 .
Если увеличить число разбиений, то при
этом уменьшится длина частичного отрезка
,
при этом
будет более точно определять площадь
трапеции. Поэтому за точное значение
площади криволинейной трапеции принимают
предел
при
.
Если увеличить число разбиений, то при
этом уменьшится длина частичного отрезка
,
при этом
будет более точно определять площадь
трапеции. Поэтому за точное значение
площади криволинейной трапеции принимают
предел
при
 :
:
 ,
то есть
,
то есть
 .
.
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.