5 Асимптоты графика функции

Определение. Асимптотой кривой называется прямая, к которой кривая неограниченно приближается по мере удаления в бесконечность.

Асимптоты бывают вертикальными, наклонными и горизонтальными.

Прямая является вертикальной асимптотой графика функции , если , или , или .

У равнение наклонной асимптоты имеет вид . Если наклонная асимптота существует, то k и b находятся по формулам:

Если хотя бы один из пределов не существует или равен бесконечности, то кривая наклонной асимптоты не имеет.

В частности, если k = 0, то . Если этот предел существует и конечен, то y=b – уравнение горизонтальной асимптоты.

Общая схема исследования функции и построения ее графика:

1) найти область определения функции;

2) найти (если возможно) точки пересечения графика с осями координат;

3) выяснить является ли функция четной, нечетной или общего вида;

4) исследовать функцию на непрерывность;

5) найти асимптоты графика функции;

6) найти экстремумы, интервалы монотонности функции;

7) найти интервалы выпуклости, вогнутости и точки перегиба графика функции;

8) на основании проведенного исследования построить график функции.

Неопределенный интеграл .1.1 Понятие неопределенного интеграла

В дифференциальном исчислении решается задача: по данной функции найти ее производную. Интегральное исчисление решает обратную задачу: найти функцию , зная ее производную.

Определение 1. Функция называется первообразной функции на интервале , если для любого выполняется равенство .

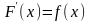Теорема 1. Если функция является первообразной функции на , то множество всех первообразных для задается формулой , где – постоянное число.

Определение 2. Множество всех первообразных функций для называется неопределенным интегралом от функции и обозначается символом ., т.о .

Здесь – подынтегральная функция, – подынтегральное выражение, – переменная интегрирования,

– знак неопределенного интеграла.

О перация нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Геометрически неопределенный интеграл представляет собой семейство параллельных кривых . График первообразной называется интегральной кривой (см. рисунок 1).

Всякая непрерывная на функция имеет на этом промежутке неопределенный интеграл. Результат интегрирования проверяется дифференцированием.

1.2 Основные свойства неопределенного интеграла

1. Производная неопределенного интеграла равна подынтегральной функции: .

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению: .

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: , в частности, .

4. Постоянный множитель можно выносить за знак интеграла: , где – .

5. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций: .

6. Если и – дифференцируемая функция, то ,

то есть формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией, имеющей непрерывную производную.

Правила интегрирования Если , то 1.) .

2.) 3) .

3. Таблица основных интегралов

1. ; 2.) ; 3) . ; 4) ;

5. ; 6) ; 7) ; 8) ;

9) ; 10) ; 11) ; 12) ;

13. ; 14) ; 15) ;

16) ; 17) ; 18) ;

19) ; 20) ;

ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

2.1 Метод непосредственного интегрирования

Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции приводится к табличному интегралу, называется непосредственным интегрированием.

Пример . Найти интеграл .

Решение: числитель почленно разделим на знаменатель и запишем данный интеграл в виде разности двух интегралов .

2.2 Метод подведения под знак дифференциала

Если подынтегральное выражение содержит некоторую функцию и ее производную, то в этом случае используют метод подведения под знак дифференциала: 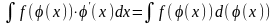. При сведении интеграла к табличному используют следующие преобразования: , b – число, , , . Например, .

2.3 Метод интегрирования подстановкой

Данный метод заключается во введении новой переменной интегрирования, при этом заданный интеграл приводится к новому интегралу, который является табличным или сводящимся к нему.

Пусть требуется вычислить интеграл , сделаем подстановку , где – монотонная, имеющая непрерывную производную функция. Тогда и формула интегрирования подстановкой будет иметь вид

.

После нахождения интеграла следует перейти от новой переменной интегрирования к старой переменной .

Пример Найти интеграл .

Решение. Сделаем подстановку , отсюда найдем , .

Итак,