Курс лекций.

1 Матрицы

Матрицей называется прямоугольная таблица, состоящая из чисел. Например:

.

В общем виде любую матрицу удобно записывать так:

.

Здесь a_ij –обозначение числа, стоящего на пересечении i–й строки и j–го столбика. Числа a_ij называются элементами матрицы. Особенно часто мы будем работать с квадратными матрицами, у которых m=n. Это число называется порядком квадратной матрицы. Можно рассматривать и матрицы, состоящие из одной строки (m=1) или из одного столбца (n=1).

Пример 1.

.

Здесь А – квадратная матрица второго порядка (m=n=2), В – матрица–строка, С – матрица–столбец. В матрице А : a₁₁ = 0, a₁₂ = 2, a₂₁ = 1, a₂₂ = –3 .

В матрице С: a₁₁ = 8, a₂₁ = –3, a₃₁ = 3 .

Матрицу любого размера, состоящую только из нулей, будем называть нулевой и обозначать буквой О:

О= .

В квадратной матрице элементы составляют так называемую главную диагональ. Другая диагональ называется побочной.

побочная диагональ

главная диагональ

Квадратная матрица называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю. На главной диагонали могут быть любые числа. Если все они равны 1, то такая диагональная матрица называется единичной. Будем всегда обозначать ее буквой Е . Итак,

E = – единичная, D = – произвольная диагональная матрица.

Научимся выполнять простые действия с матрицами.

1) Умножение матрицы на число. Чтобы умножить матрицу на число нужно все ее элементы умножить на это число. Например:

.

2) Сложение матриц.. Складывать можно только матрицы одинакового размера. Сложение выполняется поэлементно:

. Правило сложения матриц в общем виде можно записать так: если

то .

Здесь обозначение mxn указывает размеры матриц.

3) Умножение матриц.

Пусть т.е. число столбцов матрицы А равно числу строк матрицы В. Произведением AB называется матрица элементы которой вычисляются по формуле:

.

Чтобы разобраться в этой формуле и запомнить её, возьмём i–ю строчку матрицы А и j–й столбик В (они должны быть равной длины). Перемножим первые элементы строчки и столбика, вторые элементы, и так далее. Затем все полученные произведения сложим:

4) Транспонирование матриц.

Для любой матрицы А символом А^Т будем обозначать матрицу, у которой 1–й, 2–й, ... строками являются 1–й, 2–й, ... столбцы матрицы А. Итак, если то .

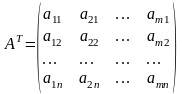Для квадратной матрицы можно сказать, что транспонирование – это отражение относительно главной диагонали.

Пример 3.

Теорема 1. Действия сложения и умножения матриц обладают следующими свойствами (для любых матриц А, В, С, с которыми эти действия можно выполнить):

(A+B)+C=A+(B+C) – ассоциативность сложения;

A+B=B+A – коммутативность сложения;

(АВ)С=А(ВС) – ассоциативность умножения;

А(В+С)=АВ+АС – дистрибутивность.

2 Определители

Определитель – это число, которое по специальным правилам вычисляется для каждой квадратной матрицы. Определитель матрицы А будем обозначать так: |A|.

Иногда определитель обозначают символом detA и называют детерминантом, но мы будем пользоваться русским термином.

Определителем матрицы 2–го порядка называется число, которое записывается и вычисляется так:

.

Пример 4. Пусть . Тогда .

Определителем матрицы 3–го порядка называется число, которое записывается и вычисляется следующим образом:

Рассмотрим внимательно эту формулу и сделаем такие наблюдения:

1) В формуле используются определители 2–го порядка, значит предполагается, что их мы вычислять уже умеем.

2) В формуле каждый элемент первой строчки умножается на определитель, который получится, если вычеркнуть строчку и столбик, где этот элемент стоит. Такой определитель будем называть минором соответствующего элемента a_ij и обозначать M_ij .

3)Перед произведением элемента а₁₂ и минора М₁₂ взят знак «». Чтобы сформулировать и запомнить правило знаков, вводится понятие алгебраического дополнения. Алгебраическим дополнением элемента a_ij называется число

.

Другими словами, алгебраическое дополнение к элементу a_ij – это минор M_ij , взятый со знаком «+», если i+j – чётное число, или со знаком «», если i+j – нечётное число.

Используя новые понятия, формулу для определителя 3–го порядка можно записать так:

.

Перейдём теперь к общему случаю. Определителем квадратной матрицы порядка n называется число, которое записывается и вычисляется следующим образом:

.

Эта формула называется разложением определителя по первой строке. Заметим, что в ней алгебраические дополнения вычисляются как определители порядка n1. Такой подход использует принцип математической индукции: зная, как вычисляются определители 3–го порядка, можно вычислять определители 4–го порядка, и так далее: формула позволяет переходить к более высоким порядкам.

Рассмотрим свойства определителей.

Свойство 1. Определитель можно вычислить с помощью разложения по любой строке или по любому столбцу, т.е. определитель равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения.

Свойство 2. При транспонировании матрицы величина ее определителя не меняется.

Доказательство. Проведем доказательство методом математической индукции по порядку определителя n.

База индукции. Для n=2 свойство 2 легко проверяется:

.

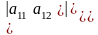Свойство 3. Если в определителе поменять местами 2 строки, то он сменит знак.

Свойство 4. Сумма произведений элементов строки на алгебраические дополнения элементов другой строки равна нулю. т.е. при i  j

Свойство 5. Определитель не изменится, если к элементам какой–либо строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Свойство 6. Определитель произведения матриц равен произведению их определителей: |AB|=|A||B|.

Это свойство мы доказывать не будем, лишь поясним на примере.

Пример 9. Пусть . Тогда

Вычислим определители:

Итак,