1. Значение научных исследований и исторические этапы развития опытного дела.

Краткая история развития опытного дела. Зарождение сельскохозяйственного опытного дела в России, в состав которой входила тогда и Беларусь, началось со второй половины 18-го века с работ Андрея Тимофеевича Болотова (1738-1833). Он один из первых показал взаимосвязь земледелия со скотоводством, предложил собственный метод инкубации яиц, издавал первые сельскохозяйственные журналы.

Михаил Георгиевич Ливанов (1751-1800) был первым ученым-зоотехником в России. В своих книгах «Руководстве к разведению и поправлению домашнего скота» (1794) и «О земледелии, скотоводстве и птицеводстве» (1799) он отмечал роль кормления и скрещивания в достижении высокой продуктивности животных.

Академик Всеволод Иванович Всеволодов (1790-1863) в 1837 году написал «Курс скотоводства», в котором обосновал научные основы животноводства, исходя из эволюционной теории.

В послеоктябрьской период научные исследования в животноводстве начали развиваться более интенсивно. В 1921 году в Москве состоялся съезд по сельскохозяйственному опытному делу, в котором приняли участие более 500 делегатов из многих регионов Союза.

Большой вклад в развитие опытного дела в животноводстве внесли выдающиеся ученые-зоотехники: Павел Николаевич Кулешов (1854-1936), Михаил Федорович Иванов (1871-1935), Николай Петрович Чирвинский (1848-1920), Илья Иванович Иванов (1870-1932), Еллий Анатольевич Богданов (1872-1932), Михаил Иудович Дьяков (1878-1952), Ефим Федорович Лискун (1873-1958), Иван Семенович Попов (1888-1964), Александр Петрович Дмитроченко (1900-1981) и др.

В Беларуси систематические научные исследования по животноводству начали проводиться с 1919 года в Горы-Горецком земледельческом институте, на базе которого в 1925 году образована Белорусская сельскохозяйственная академия (БСХА). Профессором кафедры животноводства этого вуза работал Николай Васильевич Найденов (1886-1945). Он изучал методы выращивания молодняка крупного рогатого скота в разных условиях, разрабатывал нормы и рационы кормления сельскохозяйственных животных.

В 1964 году ректором БСХА был назначен профессор Константин Михайлович Солнцев (1914-1995), а в 1977 году он возглавил Всесоюзный научно-исследовательский институт животноводства. Им разработаны теоретические основы рационального использования биологически активных веществ в кормлении сельскохозяйственных животных, выполнены работы по вопросам белкового, минерального и витаминного питания животных. Он являлся организатором промышленного производства в нашей республике кормовых добавок и их использования для обогащения комбикормов.

2. Дать определение понятию науки. Цель науки и основные методы биологических исследований (эксперимент, наблюдение и т.д.)

Нау́ка — область человеческой деятельности, направленная на выработку и систематизацию объективных знаний о действительности.

Непосредственные цели науки - описание, объяснение и предсказание процессов и явлений действительности, составляющих предмет ее изучения, на основе открываемых ею законов.

Основными из этих методов являются наблюдение и эксперимент.

Наблюдение – направленное и планомерное восприятие объектов и явлений окружающей действительности. Наблюдение – самый древний метод исследований. Наблюдая за поводками диких животных, условиями их жизни, люди приобретали знания, опыт для их одомашнивания. Первым одомашненным животным была собака. Академик Н.Я. Марр шутливо отметил, что собака вывела человека в люди.

Научное наблюдение – строится по заранее обдуманному плану, ведется систематически, имеет строго определенную задачу. Научное наблюдение включает: выбор объекта (например, коровы), определение цели (изучение поведенческих реакций), описание, выводы.

Эксперимент (от латинского experimentum – проба, опыт) – метод познания, при помощи которого в контролируемых и управляемых условиях исследуются изучаемые явления. Зоотехнический эксперимент (опыт) – это изучение ответных реакций животных в специально создаваемых, регулируемых и контролируемых условиях. Из ответных реакций в первую очередь определяют показатели продуктивности. Но чтобы установить причины изменения продуктивности, определяют физиологические, биохимические и другие показатели. По мнению академика И.П. Павлова, наблюдение собирает то, что ему предлагает природа, опыт же берет у природы то, что он хочет.

По сравнению с другими методами исследований эксперимент имеет ряд преимуществ:

в отличие от простого наблюдения он является активным методом познания, так как исследователь воздействует на подопытных животных, создает им условия, которые его интересуют;

эксперимент можно неоднократно повторять при одних и тех же или при измененных условиях и, следовательно, получать более объективные данные;

рамки эксперимента возможно расширить. Например, в медицине эксперименты над человеком недопустимы и тогда используют результаты опытов на животных – его заменителях (обезьянах, белых мышах, крысах и т.д.).

Особенность зоотехнических опытов в том, что они являются сравнительными.

3.Значение эксперимента в научных исследованиях.

Постановка и организация эксперимента определяются его назначением. Эксперименты, которые проводятся в различных отраслях науки, являются химическими, биологическими, физическими, психологическими, социальными и т. п. Они различаются по способу формирования условий (естественных и искусственных); по целям исследования (преобразующие, констатирующие, контролирующие, поисковые, решающие); по организации проведения (лабораторные, натурные, полевые, производственные и т.п.); по структуре изучаемых объектов и явлений (простые, сложные); по характеру внешних воздействий на объект исследования (вещественные, энергетические, информационные); по характеру взаимодействия средства экспериментального исследования с объектом исследования (обычный и модельный); по типу моделей, исследуемых в эксперименте (материальный и мысленный); по контролируемым величинам (пассивный и активный); по числу варьируемых факторов (однофакторный и многофакторный); по характеру изучаемых объектов или явлений (технологические, социометрические) и т. п. Конечно, для классификации могут быть использованы и другие признаки

Решающий эксперимент дает такие факты, которые согласуются с одной из гипотез и противоречат другой

Лабораторный эксперимент проводится в лабораторных условиях с применением типовых приборов, специальных моделирующих установок, стендов, оборудования и т. д.Чаще всего в лабораторном эксперименте изучается не сам объект, а его образец.

4.Виды зоотехнических опытов и их характеристика

Главная цель зоотехнических опытов – изыскать факторы, повышающие продуктивные качества животных. Для этого предложено более 10 методов постановки опытов. Но главными из них являются периодический и групповой. Остальные представляют собой разновидности группового метода или комбинированные: сочетание периодического и группового.

Периодический метод (метод периодов) разработали немецкие ученые Кюн и Вольф. Это один из первых методов, который был использован в опытной работе.

Сущность метода: действие изучаемого фактора испытывается на одной группе животных, но в разные периоды времени.

Оценка результатов опыта проводится по разности в показателях между периодами

Групповой метод предложил датский ученый Фиорд.

Сущность метода: действие изучаемого фактора испытывается на нескольких группах животных, но в одно и то же время. Следовательно, этот метод противоположен периодическому.

Метод пар-аналогов (парный метод)

Сущность метода: комплектование подопытных групп производится путем подбора аналогов сходных животных, которых распределяют таким образом, чтобы каждому животному в одной группе соответствовал аналог под этим же порядковым номером в другой группе. Если две группы, подбирают пары аналогов, если три – по три аналога под порядковыми номерами: 1-1-1, 2-2-2, 3-3-3 и т.д.

5.Структура процесса исследования

Определение объекта анализа. В процессе решения данной задачи: определяется анализируемая система управления; формируются цели и задачи управления; производится первичная декомпозиция системы с выделением управляющей подсистемы (органов управления), объектов управления и окружающей среды; при необходимости выделяются подсистемы и факторы окружающей среды, оказывающие положительное (компаньоны) и отрицательное (конкуренты) влияние на функционирование системы; устанавливаются виды и формы воздействия управляющей подсистемы и реакций объектов управления, а также воздействий окружающей среды; определяются основные требования, предъявляемые к системе, и формируется общий алгоритм функционирования, реализуемый в соответствии с заданными целями и задачами управления.  Структурный анализ. При этом детально изучается состав системы управления, устанавливаются связи и отношения между ее элементами. Результатом структурирования являются различные варианты структур анализируемой системы, позволяющие определить характеристики и отдельные частные недостатки выделенных элементов и связей между ними и наметить пути их устранения.  Функциональный анализ. При решении данной задачи исследуется динамика системы путем выявления используемых способов и алгоритмов управления, реализуемых в различных условиях обстановки и полученных при этом результатов. С учетом структурирования определяются перечень частных задач и функций каждого элемента системы, порядок их взаимодействия, необходимые входные и выходные данные.  Информационный анализ. В процессе исследования информационных характеристик определяются объемы поступающей и исходящей информации в единицу времени, в целом по системе и отдельно по основным элементам, объем информации, способы передачи и доставки информации, основные направления информационных потоков, качественный состав информации.  Параметрический анализ. При этом систематизируются частные качественные и количественные показатели структур, процессов функционирования и информации, полученные ранее, а также определяются обобщенные (интегральные) показатели, характеризующие внешние свойства анализируемой системы и ее отдельных элементов.  Оценка эффективности. При этом с целью определения достигнутых в процессе функционирования системы управления результатов и затраченных на достижение этих результатов материальных и временных ресурсов производятся вычисления количественных значений выбранных показателей эффективности, формирование критериев и оценка эффективности с помощью данных критериев.

6.Дать характеристику сущности методов одно-яйцовых двоен и пар-аналогов.

Метод однояйцовых двоен. Сущность метода в том, что пары аналогов представлены однояйцовыми двойнями, или идентичными близнецами, то есть практически одинаковыми животными. Этим самым исключается влияние индивидуальных особенностей животных на исход опыта. Поэтому животных для опыта требуется немного: достаточно 3 - 4 головы в каждой группе. Данный метод чаще используют при проведении опытов на жвачных животных: крупном рогатом скоте, овцах, козах.

Однояйцовые двойни образуются в результате оплодотворения сперматозоидом одной яйцеклетки с двумя ядрами, либо яйцеклетками с одним ядром, но сперматозоидом с двумя ядрами. Яйцеклетка может содержать и по 3, 4 и более ядер и тогда рождается соответственно 3, 4 и более однояйцовых близнецов. Но такие случаи встречаются реже.

Благодаря большой однородности между группами использование этого метода дает наиболее объективные результаты. Недостаток метода в трудности формирования групп. Можно сформировать только две группы, а следовательно, изучить только один фактор.

Метод пар-аналогов (парный метод)

Сущность метода: комплектование подопытных групп производится путем подбора аналогов сходных животных, которых распределяют таким образом, чтобы каждому животному в одной группе соответствовал аналог под этим же порядковым номером в другой группе. Если две группы, подбирают пары аналогов, если три – по три аналога под порядковыми номерами: 1-1-1, 2-2-2, 3-3-3 и т.д.

Метод пар-аналогов является основным в опытной работе. Он позволяет изучить действие различных факторов (наследственных, кормленческих, технологических и др.) на животных в течение длительного периода, то есть в динамике развивающегося организма. Поэтому этот метод дает возможность сделать более обоснованные выводы, получить более объективные данные. Недостаток метода в том, что оценка изучаемых факторов производится на разных, хотя и сходных животных, но полного сходства групп добиться невозможно. Метод требует большего числа животных, а это ведет к увеличению затрат на проведение опыта.

7. Дать характеристику сущности методов миниатюрного стада и сбалансированных групп

Метод миниатюрного, или модельного стада (министада) предложили А.П. Дмитроченко, И.Я. Гуревич, Ю.К. Олль (1958, 1965) для проведения длительных опытов по кормлению и содержанию животных.

Сущность метода: по принципу случайного отбора (жеребьевкой) формируют опытную группу (министадо), которая должна быть моделью всего стада. При формировании министада поголовье фермы (комплекса) условно распределяют на отдельные части с учетом продуктивности, физиологического состояния и от каждой из этих частей отбирают по 10 - 15 % животных в министадо.

Сформированное министадо (40 голов) является опытной группой, которая будет получать изучаемый фактор. Контролем будет служить общее стадо фермы (360 голов) Если потребуется изучить два фактора, надо сформировать два министада.

Метод сбалансированных групп применяют при

невозможности использования метода пар-аналогов. Сущность его

заключается в подборе групп животных, относительно

равноценных по основным средним показателям. Для исключения

элемента случайности число животных увеличивают в 1,5-2 раза по

сравнению с методом пар-аналогов и добиваются максимального

сходства по средним показателям. Необходимое число животных

(n) рассчитывают по формуле:

n = 2×K² × CV² \ D²

где K – константа (при Р>0,95 равна 3,29); CV – коэффициент

изменчивости (%); D – различие между средними опытных групп

(%).

Чем выше коэффициент изменчивости и меньше ожидаемые

различия между группами, тем большее число животных

необходимо в опыте для получения надежных результатов

8. Методы интегральных групп

Методы интегральных групп

Эта группа методов позволяет получить в одном

эксперименте информацию о влиянии нескольких факторов на

организм животных. Также имеется возможность установить

наиболее эффективное влияние соотношения изучаемых факторов.

Метод двухфакторного комплекса заключается в том, что

в опыте изучают влияние двух факторов одновременно при

разном их уровне (табл. 2).

2. Схема проведения опыта с использованием

2-х факторного комплекса

Группа Уровень протеина Уровень углеводов

1 высокий высокий

2 высокий низкий

3 низкий высокий

4 низкий низкий

По этой схеме можно оценить как влияние каждого фактора

в отдельности, так и их совместное взаимодействие.

Многофакторные комплексы применяют тогда, когда

требуется изучить одновременно влияние нескольких факторов

при различном их сочетании (табл. 3).

3. Схема проведения опыта с использованием

3-х факторного комплекса

Группа Уровень протеина Уровень углеводов Уровень жира

1 высокий высокий высокий

2 высокий высокий низкий

3 высокий низкий высокий

4 высокий низкий низкий

5 низкий высокий высокий

6 низкий высокий низкий

7 низкий низкий высокий

8 низкий низкий низкий

Во всех рассмотренных выше методах, кроме однояйцовых

близнецов, опытные группы животных имеют лишь, в общем, и

целом сходную, но не тождественную наследственность.

Поэтому необходимо считаться с индивидуальными

наследственными различиями в пределах пар-аналогов, и,

следовательно, с возможным взаимодействием «генотип×среда».

Слово интегральный в переводе с латинского означает неразрывно связанный, цельный, единый.

Сущность данного метода в том, что он позволяет изучить действие на животный организм каждого фактора в отдельности, а также их совместное (единое) действие в различных сочетаниях. Например, для изучения этим методом влияния добавок солей двух микроэлементов: меди и кобальта (двух факторов) в рационах поросят-отъемышей потребуется 4 подопытных групп.

Схема двухфакториального опыта

Группы	Добавки солей
	меди	кобальта
1. Контрольная	-	-
2. Опытная	+	-
3. Опытная	-	+
4. Опытная	+	+

Вторая и третья опытные группы получают по одному из изучаемых микроэлементов в отдельности, четвертая группа – оба микроэлемента. Результаты опыта оценивают по разности в показателях между каждой из опытных групп и контрольной, а также - между опытными группами.

При изучении действия трех микроэлементов меди, кобальта, йода (трех факторов) уже потребуется 8 подопытных групп.

Схема трехфакториального опыта

Группы	Добавки солей
	меди	кобальта	йода
1. Контрольная	-	-	-
2. Опытная	+	-	-
3. Опытная	-	+	-
4. Опытная	-	-	+
5. Опытная	+	+	-
6. Опытная	-	+	+
7. Опытная	+	-	+
8. Опытная	+	+	+

Опыт дает возможность определить действие каждого фактора в отдельности, выделить оптимальные сочетания их совместного действия, установить также угнетение одного фактора другим. Такой многосторонний анализ опыта отражает множественные зависимости, которые наблюдаются в природе.

Метод интегральных групп удобен и для изучения влияния разных уровней: высокого (+) и низкого (-) разных элементов питания, например, протеина и жира (двухфакториальный комплекс), протеина, жира и углеводов (трехфакториальный комплекс).

Достоинство метода в том, что он дает возможность получить большой объем научной информации, а недостаток – в громоздкости опытов: требуется большое число подопытных групп, комплектование которых представляет значительные трудности, возрастают затраты на экспериментальные исследования.

9. Дать характеристику сущности периодов, параллельных групп-периодов, параллельных групп-периодов с обратным замещением.

Метод групп-периодов. Сущность метода: с опытной группой эксперимент проводится периодическим методом. Дополнительно вводится контрольная группа, которая не получает изучаемый фактор.

Схема опыта методом групп-периодов

Группы	Предварительный период	Первый опытный период	Второй опытный период	Третий опытный период
Контрольная	ОК	ОК	ОК	ОК
Опытная	ОК	ОК	ОК+А	ОК

Об эффективности действия изучаемого фактора А, который животные второй группы получают во второй период дополнительно к основному комплексу (ОК) или вместо части его проводят сравнения по двум направлениям: по горизонтали, сравнивая показатели опытной группы между вторым периодам с первым и третьим, а также по вертикали: по разнице в показателях второго периода между опытной группой и контрольной. Наличие контрольной группы позволяет исключить влияние случайных обстоятельств на исход опыта.

Опыты этим методом проводят в основном на взрослых животных для изучения действия одного фактора.

Метод параллельных групп периодов применяется в случаях, когда одновременно изучают действие нескольких факторов, например, добавок в рацион кормовой и сахарной свеклы. В этом случае опыт проводят по следующей схеме.

Схема опыта методом параллельных групп-периодов

Группы	Предварительный период, 15 суток	Первый опытный период, 25-30 суток	Второй (главный) опытный период, 30-60 суток	Третий (заключительный) опытный период, 25-30 суток
Первая	ОР	ОР	ОР+кормовая свекла	ОР
Вторая	ОР	ОР	ОР+сахарная свекла	ОР

В схеме указана минимальная продолжительность периодов. Различие между группами в том, что во второй (главный) период одна из групп дополнительно к основному рациону (ОР) получает кормовую, а вторая – сахарную свеклу. Об эффективности действия каждого из этих корнеплодов судят по разнице в показателях продуктивности второго периода с первым и третьим внутри каждой группы, а чтобы определить, какой из корнеплодов эффективнее сравнивают показатели между первой и второй группами в главный период.

Метод используют при проведении краткосрочных опытов по кормлению сельскохозяйственных животных.

Метод групп-периодов с обратным замещением предложил профессор Е.А. Богданов для проведения опытов по кормлению на взрослых животных. В нем сочетаются положительные стороны периодического и группового методов, так как ограничивается влияние на исход опыта индивидуальных особенностей животных и фактора времени. Сущность метода в том, что каждая из опытных групп в разные периоды получает разные факторы.

Схема опыта методом групп-периодов с обратным замещением

Группа	Периоды
	уравнительный	первый опытный	второй опытный	третий опытный
Первая	ОР	ОР+А	ОР+Б	ОР+А
Вторая	ОР	ОР+Б	ОР+А	ОР+Б

Для опыта по принципу аналогов подбирают не менее 10-12 животных, которых распределяют в две равные группы. Опыт состоит из уравнительного периода длительностью 15 суток и трех опытных периодов по 25-30 суток каждый. Чтобы избежать влияние предыдущего фактора, показатели продуктивности учитывают в последние 15 суток каждого периода. Сравнение действия изучаемых факторов по этому методу проводится в двух направлениях: по горизонтали (^→_←) между периодами и по вертикали (↓↑) между группами. За короткое время этим методом удается изучить влияние на животных нескольких кормовых факторов. Группы и периоды взаимно контролируются, опыт удешевляется, повышается достоверность его результатов.

10. Дать характеристику методу повторного замещения и латинского квадрата

Метод повторного замещения предложен профессором С.С. Еленевским. При проведении опытов методом периодов нередко возникает необходимость для получения достоверных результатов провести повторные эксперименты, что связано с дополнительными затратами сил и средств.

Сущность метода повторного замещения заключается в том, что он совмещает элементы метода групп и метода групп-периодов и его нередко называют комбинированным методом. Он позволяет получать многократные данные в процессе одного эксперимента, что повышает результативность опыта. Чаще всего метод повторного замещения применяют при постановке опытов по кормлению лактирующих коров. Подбор животных для проведения опыта осуществляют методом пар-аналогов или методом сбалансированных групп.

Опыты проводят с учетом сезона года. Например, изучать питательность пастбищной травы можно только в период вегетации растений. Влияние сена, силоса, сенажа или корнеклубнеплодов на молочную продуктивность коров лучше изучать в стойловый период,

В ряде случаев продолжительность опытов в основном периоде может быть увеличена или сокращена. Лучшие результаты, как правило, получают при более продолжительном опытном периоде.

Метод повторного замещения имеет недостатки. Например, при замене одного корма другим на результаты опыта может оказать влияние последействие первого корма, и не всегда можно эквивалентно заменить один корм другим.

Метод латинского квадрата является логическим развитием метода групп-периодов. Он предложен в 50-х годах 20-го века. Латинский квадрат в математике – это квадратная таблица, каждая строка и каждый столбец которой содержит одни и те же числа.

Примеры латинских квадратов

1	2	3		1	2	3	4
2	3	1		2	1	4	3
3	1	2		3	4	1	2
				4	3	2	1

Сущность постановки опытов методом латинского квадрата в том, что каждая группа последовательно получает изучаемые факторы таким образом, что в один и тот же период животные разных групп получают разные факторы.

Схема постановки опытов методом латинского квадрата

Для двух групп (факторов) и двух периодов

Для трех групп (факторов) и трех периодов

Для четырех групп (факторов) и четырех периодов

Группы

Периоды

Группы

Периоды

Группы

Периоды

1

2

1

2

3

1

2

3

4

1

А

В

1

А

В

С

1

А

В

С

D

2

В

А

2

В

С

А

2

В

А

D

С

3

С

А

В

3

С

D

А

В

4

D

С

В

А

Буквами (А, В, С, D) означают изучаемые факторы и периоды опыта, когда группы получают эти факторы. При постановке опытов методом латинского квадрата необходимы следующие условия:

• число периодов должно соответствовать числу изучаемых факторов и числу групп;

• число животных в опыте должно быть кратным числу периодов опыта, или числу изучаемых факторов. Например, при трех периодах – 3, 6, 9, при четырех – 4, 8, 12 и т.д. Это значит, что в каждой группе будет по 1, 2, 3 и т.д. животных;

• все подопытные животные должны быть сохранены до конца опыта, в противном случае сильно осложняется математическая обработка;

• для опыта отбирают животных–аналогов и распределяют по группам по принципу случайности;

• в начале опыта – уравнительный период, когда животные всех групп получают основной комплекс (ОК), или основной рацион (ОР). В опытные периоды каждая из групп последовательно дополнительно к основному комплексу получает изучаемые факторы.

Достоинства метода: опыты проводят на небольшом числе животных непродолжительное время и получают обширную научную информацию. Можно изучить действие четырех факторов имея всего четырех животных – аналогов. Метод в несколько раз ускоряет проведение опытной работы в животноводстве.

Недостатки метода: последствие предыдущего фактора. Чтобы ограничить это действие предлагают в первую треть каждого периода продуктивность не учитывать. Например, продолжительность периодов по три недели. Учет проводят в последние две недели. Метод непригоден для длительных опытов, когда изучаются показатели роста, развития, воспроизводства и др. Поэтому метод латинского квадрата используется в основном в кратковременных опытах на лактирующих коровах.

11.Методы определения перевариваемости корма

Перевариваемость корма – один из важнейших показателей его ценности. Животные живут только с той части корма, которую могут переварить. Непереварившиеся вещества корма выделяются из организма.

Понятие перевариваемости

Из съеденного количества корма часть выделяется с навозом. Та часть корма, которая не выделилась с навозом определяется как перевариваемая.

Например,

Употребленное органическое вещество в корме      10 кг сухого вещества

минус органическое вещество в навозе                      4 кг сухого вещества

равно перевариваемое органическое вещество         6 кг сухого вещества

= 60% органического вещества корма

Выраженная в процентах перевариваемость называется коэффициентом перевариваемости.

Влияние на перевариваемость

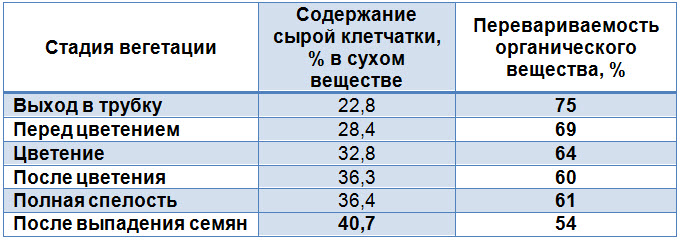
Перевариваемость корма – это ни в коем случае не постоянная величина, она зависит от различных факторов, таких как вид животных, количество корма, состав рациона и подготовка кормов. Самые большие различия между видами животных наблюдаются по сырой клетчатке. Жвачные намного превосходят свиней по возможностям переваривания богатых сырой клетчаткой кормов. На то, какое количество сырой клетчатки будет съедено животными, влияет не только перевариваемость сырой клетчатки, но и перевариваемость других питательных веществ.

Как у жвачных, так и у моногастричных животных перевариваемость корма снижается с увеличением количества сырой клетчатки в нем.

Перевариваемость органической массы некоторых кормов у КРС и свиней

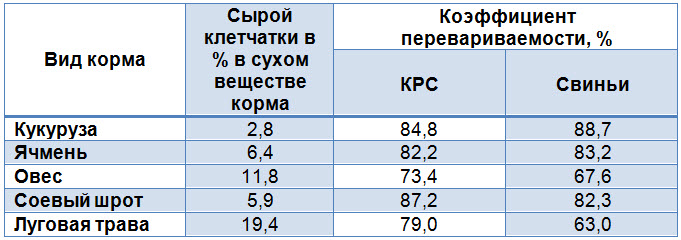
Стадия вегитации и перевариваемость зеленой массы у КРС

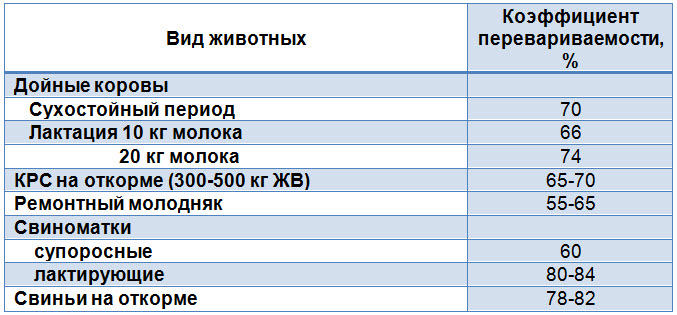
Требования по перевариваемости корма

Поскольку потребность животных в питательных веществах увеличивается вместе с растущей продуктивностью, а ёмкость пищеварительного тракта является ограниченной, необходимо увеличивать концентрацию питательных веществ в рационе с увеличивающейся продуктивностью животного. То есть в одинаковом объёме корма должно содержаться больше питательных веществ. Что означает, что перевариваемость органического вещества рациона высокопродуктивных животных должна быть выше.

 Требования по перевариваемости корма для КРС и свиней 

Как определить перевариваемость корма

Классический метод определения перевариваемости – это проведение опытов с животными.

Но для повседневной практики определение перевариваемости таким путем является слишком затратным. Поэтому были разработаны различные методы, которые позволяют исследовать большое количество небольших по объёму проб за короткое время (применяются в лабораториях).

Например, при использовании ферментативного метода (ELOS-Test) с помощью реагента воссоздается и стимулируется процесс переваривания корма в рубце. Через неделю протекания реакции можно определить процент перевариваемости органической массы корма. Но и этот метод является довольно затратным, поэтому не все лаборатории его используют.

Еще одно направление в оценке перевариваемости органической массы и питательных веществ корма  – это определение ее с помощью формул на основании данных химического состава корма. Так по содержанию в корме сухого вещества можно оценить перевариваемость органической массы для разных видов животных.

Формулы для расчета перевариваемости органической массы (у, в %) в зависимости от содержания сырой клетчатки в сухом веществе корма

Формулы для расчета перевариваемости корма

Для жвачных и моногастричных животных разработаны уравнения для определения перевариваемости с учетом различных питательных веществ корма.

12. Дать определение понятиям генеральная совокупность и выборка. Какие выборки называются большими, какие малыми.

Генеральная совокупность, генеральная выборка - совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.

Генеральная совокупность состоит из всех объектов, которые имеют качества, свойства, интересующие исследователя.

Выборка или выборочная совокупность — часть генеральной совокупности элементов, которая охватывается наблюдением.

Характеристики выборки:

Качественная характеристика выборки — что именно мы выбираем и какие способы построения выборки мы для этого используем.

Количественная характеристика выборки — сколько случаев выбираем, другими словами объём выборки.

Необходимость выборки

Объект исследования очень обширный. Например, потребители продукции глобальной компании — огромное количество территориально разбросанных рынков.

Существует необходимость в сборе первичной информации.

Выборки, объем которых меньше 20—30 единиц совокупности, будем называть малыми (Четкой границы между большой и малой выборками в общем случае указать невозможно. Выборка, сделанная из совокупности с небольшим разбросом признака, может считаться большой, тогда как выборка такого же объема, произведенная из более разнородной совокупности, окажется малой. Вопрос о том, к какой категории отнести выборку, решается в каждом конкретном случае). Для расчета ошибок таких выборок используется несколько иной математический аппарат.

Средняя ошибка малой выборки вычисляется по формуле

                       (5.14)

где S — оценка среднего квадратического отклонения в генеральной совокупности по малой выборке. Она равна:

           

13. Как вычесляется средняя арифматическая в выборках

Определение средних значений изучаемого признака. Как уже отмечалось, зоотехнические опыты являются сравнительными. В них сравнивают между собой группы и периоды, то есть средние величины изучаемых признаков. В зависимости от цели исследования определяют несколько средних величин: среднюю арифметическую, взвешенную среднюю арифметическую, среднюю гармоническую и др.

Средняя арифметическая – наиболее характерное значение признака для данной совокупности (группы), ее математический центр тяжести.

Среднюю арифметическую определяют по формуле: где   – средняя арифметическая, ранее обозначали буквой М; – значения признака для каждого члена совокупности (варианты), ранее обозначали буквой V;n – общее число членов совокупности (группы) (сигма – греческая прописная буква) – знак суммирования.

Например, в группе из 5 коров среднесуточный удой отдельных животных составил, кг: 10,5; 9,7; 13,5; 14,0; 12,3.

Чтобы вычислить среднюю арифметическую для этой группы, подставим данные в вышеприведенную формулу:

Для больших выборок, когда число особей более 30, раньше применяли непрямой способ вычисления средней арифметической. Для этого предварительно строили вариационные ряды. При использовании компьютеров необходимость в этом отпала.

Основные свойства средней арифметической:

• она характеризует совокупность (группу) в целом, а не отдельных ее членов;

• средняя арифметическая величина абстрактная, то есть может не совпадать ни с одной вариантой и иметь дробную величину. Например, в группе на свиноматку за год получено 1,7 опороса. Но ведь от каждой свиноматки можно получить или один, или два опороса за год;

• среднюю арифметическую применяют для характеристики однородной совокупности. Например, среднюю живую массу определяют по отдельным половозрастным группам.

Взвешенная средняя арифметическая определяется, когда разный математический вес признака. Например, требуется определить среднее содержание переваримого протеина в 1 кг смеси, состоящей из 70 кг ячменя и 30 кг гороха, если в 1 кг ячменя содержится 75 г переваримого протеина, а в 1 кг гороха – 210 г.

Взвешенную среднюю рассчитывают по формуле:

где  – значение признака (варианта);

– математический вес признака.

Чтобы рассчитать взвешенную среднюю арифметическую, каждое значение признака умножают на его вес, все эти произведения суммируют и полученный результат делят на сумму весов.Взвешенную среднюю применяют в зоотехнии часто, например, при определении процента жира молока за лактацию.

14. Показатели, характеризующие разнообразие признаков

Признаки, или переменные, могут принимать различные конкретные значения .Различают следующие виды признаков:

Качественные или номинальные– не поддающиеся непосредственному измерения, например, характеристики пациента: диагноз, пол, профессия, семейное положение. Качественные данные, которые могут быть отнесены только к двум противоположным категориям да – нет, принимающие одно из двух значений (выжил – умер; курит – не курит)) называютсядихотомическими  .

Порядковые или ранжируемые – эти признаки можно расположить в естественном порядке (ранжировать), но при этом отсутствует количественная мера расстояния между величинами. Примером являются оценка тяжести состояния пациента, стадия болезни, самооценка состояния здоровья. При этом допускается, что тяжелое течение заболевания «хуже», чем среднетяжелое, а очень тяжелое – «еще хуже», однако нельзя сказать во сколько или на сколько хуже. Можно сказать, что порядковые данные занимают промежуточное положение между количественными и качественными типами. Их можно упорядочить как количественные данные, но над ними нельзя производить арифметические действия, как над качественными данными.

Количественные или интервальные– признаки, количественная мера которых четко определена; наиболее удобный для статистического анализа тип данных.

Количественные признаки могут быть

Непрерывными , принимающими любое значение на непрерывной шкале, например масса тела, температура, биохимические показатели крови;

дискретными , принимающие лишь определенные значения из диапозона измерения, обычно целые, например, число рецидивов, число детей в семье, число заболеваний у одного больного, число выкуриваемых сигарет.

15. Как вычисляется среднее арифметическое отклонение в больших и малых выборках?

Наиболее полную характеристику разнообразия признака в статистической совокупности дает среднее квадратическое отклонение δ, которое является общей мерой отклонения вариант от своей средней.

Расчет среднего квадратического отклонения осуществляется в определенной последовательности и включает пять этапов:

1. Определение средней арифметической (М).2. Расчет истинного отклонения (d) каждой варианты от средней величины (v — M).3. Возведение каждого отклонения в квадрат (d²) (если в исследуемой совокупности некоторые варианты встречаются неоднократно (р>1), следующим шагом необходимо умножить размер отклонения этих вариант, возведенного в квадрат (d²), на их частоту (р)).4. Определение суммы (∑ d² или ∑d²р)5. Расчет среднего квадратического отклонения ( по формуле.

Вычисление среднего квадратического (стандартного) отклонения

При анализе статистической совокупности одним из важных показателей является расположение значений элементов совокупности вокруг среднего значения (варьирование). Для характеристики варьирования в практике исследовательской работы рассчитывают среднее квадратическое (или стандартное) отклонение, которое отражает степень отклонения результатов от среднего значения, выражается в тех же единицах измерения.

Стандартное отклонение обозначается знаком   (сигма) и вычисляется по формуле:

где   -   )  - сумма разности квадратов между каждым показателем и средней арифметической величиной (сумма квадратов отклонений);

 - объем выборки (число измерений или испытуемых).

Если число измерений не более 30, т.е.  30, используется формула:

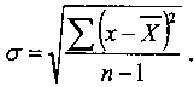
Порядок вычислений (1 вариант):

1. Заполнить первые две колонки таблицы расчетов (вычисление стандартного отклонения на примере показателей шести результатов измерения кистевой динамометрии).

Таблица 2

Вычисление среднего квадратического отклонения

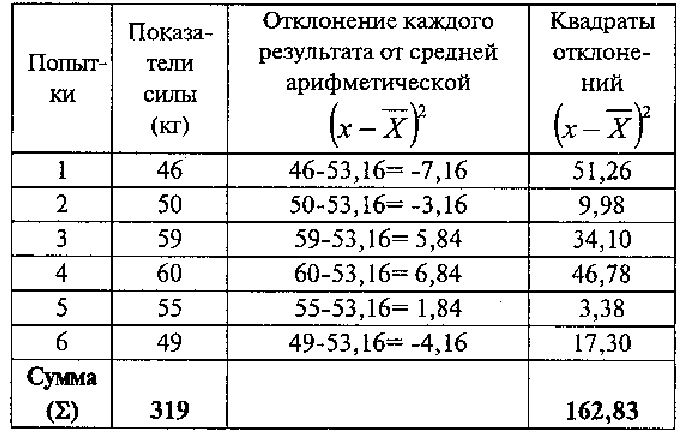
2. Рассчитать среднюю арифметическую величину:

3. Вычислить разность между каждым показателем и данной средней (третья колонка таблицы).

4. Полученные разности возвести в квадрат и суммировать (четвертая колонка таблицы).

5. Вычислить среднее квадратическое отклонение по формуле:

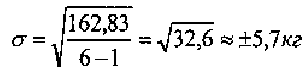
Среднее квадратическое отклонение (δ – сигма) основной показатель изменчивости. Его определяют по формуле:

В знаменателе данной формулы разница n-1 – это число степеней свободы, или число элементов свободного разнообразия. Так, если потребуется составить сумму из трех чисел, равную 100, то первые два числа могут быть любыми. Например, 50 и 30 или 500 и 300, а третье число должно быть одно: в первом случае – 20; (50 + 30 + 20 = 100), во втором – минус 700; (500 + 300 + (-700) = 100. При вычислении сигмы имеется одно ограничение. Оно определяется для группы, имеющей определенную среднюю арифметическую. Наличие в формуле знаков «+» и «-» указывает на то, что этот показатель характеризует изменчивость признака как в сторону увеличения от средней арифметической, так и в сторону уменьшения. Приведем пример расчета по количеству поросят в помете 5 свиноматок. Для этого удобнее пользоваться таблицей. В первую графу таблицы записывают варианты (в данном примере численность пометов), во вторую – отклонение каждой варианты от средней арифметической  , в третью – квадраты отклонений .

5. Пример вычисления среднего квадратического отклонения

Число поросят в помете, голов	Отклонение	Квадраты отклонений
10	-1	1
9	-2	4
12	+1	1
11	0	0
13	+2	4

Величина лимита в данной совокупности составляет: 13 – 9 = 4, а среднее квадратическое равно:

Сигма показывает среднее отклонение каждой варианты от средней арифметической. При нормальном распределении особей совокупности в пределах ±1δ находится приблизительно 68 % особей, ±2δ – 95 % и ±3δ– 99,7 %. Это значит, что практически вся изменчивость признака укладывается от средней арифметической в пределах ±3δ (правило трех сигм). Если особь не укладывается в эти пределы по основным признакам, значит, она является не типичной для данной группы. Эту особенность учитывают при комплектовании подопытных групп. Чем больше сигма, тем выше изменчивость признака.

Сигма и средняя арифметическая имеют одну и ту же единицу измерения. А если требуется сравнить изменчивость признаков, выраженных в разных единицах измерения, определяют коэффициент вариации  по формуле: 

16. Как вычисляется коэффициент вариации и что он показывает

Вариа́ция — различие значений какого-либо признака у разных единиц совокупности за один и тот же промежуток времени. Причиной возникновения вариации являются различные условия существования разных единиц совокупности. Вариация — необходимое условие существования и развития массовых явлений.Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах. Он вычисляется по формуле: ,где   - искомый показатель,  - среднее квадратичное отклонение,  - средняя величина.

 

• коэффициент вариации:

Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет её средний разброс. Исчисляется в процентах. Вычисляется только для количественных данных. В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности.

17. Какие показатели применяют для измерения связи между признаками

Слово «корреляция» (от английского correlation) означает соотношение, соответствие. Оно удачно отражает особенность зависимости, при которой определенному значению одного факторного признака может соответствовать несколько значений результативного признака (показателя). На основе этих значений можно определить среднюю величину последнего, соответствующую каждому конкретному значению факторного признака.

Коэффициент корреляции - это математическая мера корреляции двух величин. В том случае, когдаизменение одной из величин не приводит к закономерному изменению другой величины, то можно говоритьоб отсутствии корреляции между этими величинами. Коэффициенты корреляции могут бытьположительными и отрицательными. Если при увеличении значения одной величины происходитуменьшение значений другой величины, то их коэффициент корреляции отрицательный. В случае, когдаувеличение значений первого объекта наблюдения приводит к увеличениям значения второго объекта, томожно говорить о положительном коэффициенте

Связь, при которой разным значениям факторного признака соответствуют различные средние значения результативного признака называется корреляционной. Именно корреляционные связи наиболее часто используются при исследовании общественных явлений.

Суть корреляционной зависимости сводится к тому, что, с изменением значения признака х закономерным образом изменяется среднее значение признака у, в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений.

По направлению различают прямые и обратные связи. При прямой связи с ростом факторного признака растет и результативный признак. При обратной связи с увеличением факторного признака результативный уменьшается или наоборот. Например, рост производительности труда приводит к снижению себестоимости единицы продукции.

Корреляционная таблица строится по типу «шахматной», т.е. в подлежащем таблицы выделяются группы по факторному признаку х, в сказуемом – по результативному у или наоборот, а в клетках таблицы на пересечении х и у показано число случаев совпадения каждого значения х с соответствующим значением у.

Метод корреляционных таблиц применим не только к количественным, но и к описательным (качественным) признакам, взаимосвязи между которыми часто приходится изучать при проведении различных социологических исследований путем опросов или анкетирования. В этом случае такие таблицы называют таблицами сопряженности. Они могут иметь различную размерность. Простейшая размерность – 2х2 (таблица «четырех полей»), когда по альтернативному признаку («да» – «нет», «хорошо» – «плохо» и т.д.) выделяются 2 группы.

корреляционном анализе недостаточно лишь выявить тем или иным методом наличие связи между исследуемыми показателями. Теснота такой связи может быть различной, поэтому весьма важно ее измерить, т.е. определить меру связи в каждом конкретном случае. В статистике для этой цели разработан ряд показателей (коэффициентов), используемых как для количественных, так и для качественных признаков.

Для измерения тесноты связи между группировочными признаками в таблицах взаимной сопряженности могут быть использованы такие показатели, как коэффициент ассоциации и контингенции (для «четырехклеточных таблиц»), а также коэффициенты взаимной сопряженности Пирсона и Чупрова (для таблиц любой размерности).

Применительно к таблице «четырех полей», частоты которых можно обозначить через a, b, c, d, коэффициент ассоциации (Д. Юла) выражается формулой (158):

. (158)

Его существенный недостаток: если в одной из четырех клеток отсутствует частота (т.е. равна 0), то  1, и тем самым преувеличена мера действительной связи.

Чтобы этого избежать, предлагается (К. Пирсоном) другой показатель – коэффициент контингенции[53]:

. (159)

Рассчитаем коэффициенты (158) и (159) для нашего примера (таблица 48):

; 

Связь считается достаточно значительной и подтвержденной, если  >0,5 или  >0,3.

Поэтому в нашем примере оба коэффициента характеризуют достаточно большую обратную зависимость между исследуемыми признаками.

Теснота связи между 2 и более признаками измеряется с помощью коэффициентов взаимной сопряженности Пирсона (160) или Чупрова (161), рассчитываемых на основе показателя χ² :

, (160)   (161)

В нашем примере  . Рассчитывать коэффициент Чупрова для таблицы «четырех полей» не рекомендуется, так как при числе степеней свободы ν=(2-1)(2-1)=1 он будет больше коэффициента Пирсона (в нашем примере К_Ч=0,54). Для таблиц же большей размерности всегда К_Ч<К_П.

18. Как вычисляют коэффициент корреляции в больших и малых выборках?

На практике часто наблюдают не один, а два взаимосвязанных между собой признака. Например: температура воздуха и скорость ветра, высота и толщина стволов деревьев, количество выпавших осадков и число солнечных дней, взаимосвязь между индивидуально-психологическими характеристиками личности и стилем их поведения и т. д. между этими показателями существуют определенные взаимосвязи. Значение средней величины одного признака изменяется при изменении другого признака.

Различают два типа зависимостей: функциональную и стохастическую.

При функциональной связи каждой независимой переменной х соответствует вполне определенное значение зависимой переменной у.

Когда определенному значению независимого признака х соответствует несколько значений другого признака у, зависимость приобретает стохастический характер. Взаимосвязи между варьирующими признаками называется корреляцией.

В теории корреляция решаются две основные задачи: 1)определяют зависимость между случайными величинами в виде формулы; 2)определяют силу и тесноту этой зависимости.

Корреляцию подразделяют по направлению, форме и числу связей.

I. По направлению корреляция может быть прямой и обратной.При прямой корреляции с увеличением значения признака х увеличивается значение признака у. При обратной корреляции с увеличением значения признака х, значение признака у уменьшается.II.По форме корреляция бывает линейной и криволинейной.Линейная корреляция имеет место, когда с увеличением признака х соответственно увеличивается признак у.При криволинейной корреляции значение х и у изменяется сначала в одном направлении, затем в противоположном.III. По числу связей корреляция бывает простой, (когда имеется связь между двумя признаками) и множественной (имеется связь трех и более признаков.IV. По силе связи корреляция бывает сильной, средней и слабой.

Если некоторые пары чисел повторяются, можно составить корреляционную таблицу – такую таблицу, в которой результаты наблюдений записываются в порядке возрастания с указанием частот.

у х						Σ
Σ

Выборочным коэффициентом корреляции называется отношение выборочного корреляционного момента к произведению выборочных средних квадратических отклонений этих величин:

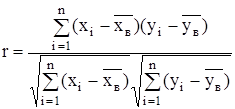
Коэффициент корреляции показывает тесноту и направление связи.

Свойства выборочного коэффициента корреляции:

1. значения коэффициента корреляции изменяются на множестве r   [-1;1];

2. чем больше абсолютное значение коэффициента корреляции, тем теснее связь между изученными признаками;

3. если коэффициент корреляции равен 0 (k=0), то между изученными признаками нет линейной корреляционной зависимости,

если |k|=1, то связь полная;

если 0,7<|k|<0,99, то связь сильная;

если 0,3<|k|<0,7, то связь средняя;

если |k|<0,3, то связь слабая.

Если r   [-1;0), то связь обратная;

если r   (0;1] – зависимость прямая.

 

Пример : У двенадцати испытуемых, участвующих в эксперименте по заучиванию чисел и слов, были получены следующие результаты: числа (X)5,5,6,3,6,7,2,5,4,3,5,4;

Слова (Y)- 4,3,4,5,4,2,4,33,6,5,6. Найти коэффициент корреляции.

Решение. Составим вспомогательную таблицу:

 

№	Числа (х)	Слова (у)	(   )		(   )·	(   )2	2
			1,58	0,12	0,199	2,49	0,014
			1,58	1,12	0,456	2,49	1,254
			2,58	0,12	0,310	6,65	0,014
			-1,58	1,12	-1,770	2,49	1,254
			2,58	0,12	0,310	6,65	1,254
			3,58	-2,12	-7,58	12,81	4,494
			-2,58	0,12	-0,310	6,65	0,014
			1,58	-1,12	- 1,770	2,49	1,254
			0,58	-1,12	-0,654	0,33	1,254
			-1,58	2,12	-3,330	2,49	4,494
			1,58	1,12	0,456	2,49	1,254
			0,58	2,12	1,230	0,33	4,494
∑					18,375	48,36	21,048

 ; 

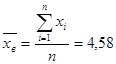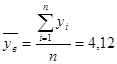
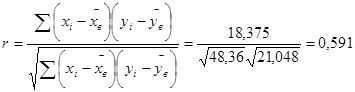
Вывод: Между запоминанием чисел и слов существует средняя прямая связь.

19. О чём говорит положительная и отрицательная связь между признаками?

Коэффициент корреляции (лат. correlatio – соотношение, взаимосвязь) – определяет величину и направление связи между признаками. Величина этого коэффициента (r) выражается в пределах от 0 до ± 1. Наличие знака «+» означает, что между признаками существует положительная корреляция, когда при увеличении одного признака другой также возрастает или, наоборот, при уменьшении одного признака другой также снижается. Если коэффициент корреляции со знаком «-», это указывает на отрицательную (обратную) связь, когда увеличение одного признака сопровождается уменьшением другого.Чем ближе показатель к единице, тем сильнее связь между признаками. При r=0,1-0,3 связь считается слабой, в пределах 0,3-0,5 – умеренной, 0,5-0,7 – заметной, 0,7-0,9 – высокой и 0,9-0,99 – весьма высокой. Например, в опыте установлена умеренная положительная связь (r = +0,36) между скоростью молокоотдачи и суточным удоем коров голландской породы.

20. С какой целью используется коээфициент регрессии и как он расчитывается.

Коэффициенты регрессии показывают интенсивность влияния факторов на результативный показатель. Если проведена предвари­тельная стандартизация факторных показателей, то b₀ равняется сред­нему значению результативного показателя в совокупности. Коэффици­енты b₁, b₂, ..., b_n показывают, на сколько единиц уровень результативно­го показателя отклоняется от своего среднего значения, если значения факторного показателя отклоняются от среднего, равного нулю, на одно стандартное отклонение. Таким образом, коэффициенты регрессии ха­рактеризуют степень значимости отдельных факторов для повышения уровня результативного показателя. Конкретные значения коэффициен­тов регрессии определяют по эмпирическим данным согласно методу наименьших квадратов (в результате решения систем нормальных урав­нений).

Аналитические достоинства регрессионных моделей заключаются в том, что, во-первых, точно определяется фактор, по которому выявля­ются резервы повышения результативности хозяйственной деятельно­сти; во-вторых, выявляются объекты с более высоким уровнем эффек­тивности; в-третьих, возникает возможность количественно измерить экономический эффект от внедрения передового опыта, проведения организационно-технических мероприятий.

При наличии корреляционной связи между факторными и результативными признаками врачам нередко приходится устанавливать, на какую величину может измениться значение одного признака при изменении другого на общепринятую или установленную самим исследователем единицу измерения.

Например, как изменится масса тела школьников 1-го класса (девочек или мальчиков), если рост их увеличится на 1 см. В этих целях применяется метод регрессионного анализа.

Наиболее часто метод регрессионного анализа применяется для разработки нормативных шкал и стандартов физического развития.

1. Определение регрессии. Регрессия — функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым.С этой целью применяется коэффициент регрессии и целый ряд других параметров. Например, можно рассчитать число простудных заболеваний в среднем при определенных значениях среднемесячной температуры воздуха в осенне-зимний период.Определение коэффициента регрессии. Коэффициент регрессии — абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого связанного с ним признака на установленную единицу измерения. Формула коэффициента регрессии. R_у/х = r_ху x (σ_у / σ_x) где R_у/х - коэффициент регрессии; r_ху - коэффициент корреляции между признаками х и у;  (σ_у и σ_x) — среднеквадратические отклонения признаков x и у.

21. Как вычисляют ошибку средней арифметической

Эта ошибка определяется по формуле:  ,из которой видно, что чем больше разнообразие признака (величина σ), тем больше ошибка. Если бы все объекты были одинаковы, то есть разнообразие было бы равно нулю, то и ошибка была бы равна нулю (m = 0)..Ошибка также зависит от численности выборки n: чем больше численность, тем меньше ошибка. Определив ошибку репрезентативности m, можно найти генеральную среднюю по формуле: , где  – генеральная средняя,M – выборочная средняя,m – ошибка репрезентативности или просто ошибка,t – критерий Стьюдента, соответствующий вероятности получаемого результата.Точное значение генеральной средней найти невозможно, поскольку число объектов стремится к бесконечности. С помощью данной формулы с определенной степенью вероятности находятся две границы: максимального и минимального значений.

22. Как определяют достоверность разницы между выборочными средними арифметическими