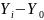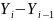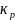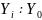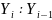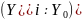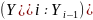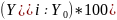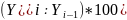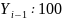Конкретное значение моды для интервального ряда определяется формулой:

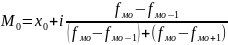, где

– Нижняя граница модального интервала;

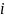– величина модального интервала;

– частота модального интервала;

– частота интервала, предшествующего модальному;

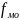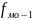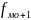– частота интервала, следующего за модальным.

Пример. Определить моду продолжительности стажа работы работников торгового предприятия, используя данные таблицы 27.

Таблица 27 Распределение работников торгового предприятия по продолжительности стажа работы

Группы рабочих продолжительности	Число работников,
стажа работы, лет	чел.
До 2	4
2-4	23
4-6	20
6-8	35
8-10	11
Свыше 10	7
Итого:	100

Решение. Модальным интервалом величины стажа работни­ков торгового предприятия будет интервал от 6 до 8 лет, так как этот интервал имеет наибольшую частоту (35 человек).

Тогда мода продолжительности стажа работы работников торгового предприятия составит:

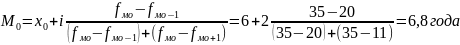
Наибольшее число рабочих имеют трудовой стаж в размере 6,8 года.

Медианой (Me), или серединным вариантом, в статистике на­зывают значение варьирующего признака, который находится в середине ряда значений, расположенных в порядке возрастания или убывания.

Для дискретного ранжированного ряда (то есть построенно­го в порядке возрастания или убывания индивидуальных вели­чин) с нечетным числом членов медианой является варианта, рас­положенная в центре ряда.

Пример Процент выполнения плана товарооборота за месяц 13 торговых предприятий составил (%): 95; 98; 101; 104; 109; 115; 119; 126; 135; 144; 176; 202; 223. Определить медиану.

Решение. Медианой здесь будет 7-я варианта, которая делит упорядоченный ряд пополам и соответствует 119 % выполнения плана товарооборота.

Для дискретного ранжированного ряда с четным числом членов медианой будет 'варианта, рассчитанная из двух смежных центральных вариант.

В интервальном вариационном ряду порядок нахождения ме­дианы следующий: располагаем индивидуальные значения при­знака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах нахо­дим медианный интервал.

Медианы в интервальном ряду распреде­ления определяется по формуле:

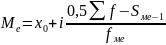
– Нижняя граница медианного интервала;

– величина медианного интервала;

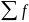– cумма частот;

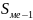– сумма накопленных частот, предшествующих медианному интервалу;

– частота медианного интервала;

Пример. По данным типового примера 6.7 (табл. 6.5) необходимо рассчитать медиану.

Решение. Медианным интервалом величины стажа работни­ков торгового предприятия будет интервал от 6 до 8 лет, так как этот интервал имеет накопленную частоту (82 = 4 + 23 + 20 + 35), которая больше половины всей суммы частот ряда (50 = 100 : 2).

Тогда медиана продолжительности стажа работы работников торгового предприятия составит:

Более половины рабочих имеют трудовой стаж в размере менее 6,2 года, остальные рабочие более 6,2 года.

Задачи для самостоятельного решения:

Задача 7.1

Распределение работников фирм по размеру среднемесячной заработной платы характеризуется следующими данными:

Таблица 28 Исходные данные.

Среднемесячная заработная плата	Число работников фирмы
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
До 3000 3000-3500 3500-4000 4000-4500 4500-5000 5000 и более	5 4 8 6 10 5	10 12 11 14 16 8	10 5 6 8 10 5	8 9 11 12 14 5	16 10 14 12 14 8	12 14 16 20 18 6	5 6 12 10 8 3	6 10 11 13 15 8	5 12 14 16 10 8	3 2 5 6 10 5	4 12 10 15 10 10	6 18 20 20 12 8	8 10 12 8 10 5	10 20 22 24 15 6	8 12 10 13 15 5

Вычислите по фирме:

1. Среднемесячную зарплату.

2. Моду и медиану.

3. Размах вариации, среднее линейное отклонение, дисперсию, среднее квадратичное отклонение.

4. Коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации?

Задание 2

Вопросы для самоконтроля:

1. Определение моды в вариационном ряду.

2. Определение моды в интервальном ряду

3. Определение медианы в вариационном ряду.

4. Определение медианы в интервальном ряду.?

5. Абсолютные показатели вариации.

6. Относительные показатели вариации

Литература: Егоров Л.И. «Статистика» стр. 66-85

Шмойлова Р.А. «Практикум по теории статистики» стр.100,124-169.

Домашнее задание: подготовиться к проверочному тесту по пройденному материалу.

Практическая работа № 9

Тема: «Расчет показателей рядов динамики»

Цель работы: Углубить и закрепить теоретические знания по теме: «Ряды динамики», Уметь определять основные показатели динамического ряда, её средние характеристики.

После изучения темы студент должен:

Знать:

• технику расчета статистических показателей, характеризующих социально-экономические явления;

Уметь:

• выполнять расчеты статистических показателей и формулировать основные выводы;

Ключевые слова и термины: Ряд динамики, абсолютный прирост, темп роста. Темп прироста, абсолютное значение одного процента прироста, средний уровень ряда, средний абсолютный прирост, средний темп роста.

Программа работы:

Задание 1.

Решите задачи

На оценку «удовлетворительно» 9.1 (без выводов)

На оценку «хорошо» 9.1(с выводами)

На оценку «отлично» 9.1; 9.2;

Методические указания к проведению практической работы:

Ряд динамики — это числовые значения статистических показателей, изменяющихся во времени и расположенных в хронологической последовательности.

Ряд динамики включает два обязательных элемента:

1. период времени, за который или по состоянию на который приводятся цифровые значения (показатель времени t);

2. конкретные числовые значения показателя, характеризующие изучаемый объект или явление (уровни ряда у).

Существуют различные виды рядов динамики. Их можно классифицировать по:

1. форме представления уровней — ряды абсолютных, отно­сительных или средних величин;

2. интервалам времени или расстоянию между уровнями — равномерные и неравномерные (равноотстоящие и неравноотстоящие);

3. по наличию основной тенденции изучаемого процесса — стационарные и нестационарные ряды;

4. показателю времени — моментные и интервальные.

Важнейшим условием правильного построения рядов дина­мики, получения правильных выводов при анализе и прогнозиро­вании его уровней является сопоставимость уровней, образую­щих ряд. Статистические данные должны быть сопоставимы: по кругу охватываемых объектов, времени регистрации, территории, идеологии расчета и ценам.

1. Сопоставимость по кругу охватываемых явлений означает сравнение совокупностей с равным числом элементов, которые должны быть однородны по экономическому содержанию и гра­ницам объекта. Несопоставимость может возникнуть в результате перехода ряда объектов из одного подчинения в другое.

2. Сопоставимость по времени регистрации для интервальных рядов обеспечивается равенством периодов времени, за которые получают данные. Для приведения рядов динамики к сопоставимо­му виду выделяют среднедневные показатели по декадам, кварта­лам, месяцам, которые затем сравнивают. Для моментных рядов ди­намики показатели следует проводить на одну и ту же дату.

Сопоставимость по территории предполагает одни и те же территориальные границы. Данные по странам и регионам границы которых изменились, должны быть пересчитаны в ста­рых пределах.

4. Сопоставимость по методологии расчетов характеризует­ся тем, что при определении уровней динамического ряда необхо­димо использовать единую методологию их расчета.

5. Сопоставимость по ценам. При приведении к сопостави­мому виду продукции, которая была измерена в стоимостных по­казателях, трудность заключается в том, что, во-первых, с течени­ем времени происходит непрерывное изменение цен, а во-вторых, существует несколько видов цен. Поэтому на практике количество продукции, произведенную в разные периоды, оценивают в ценах одного и того же базисного периода, которые называют неизмен­ными или сопоставимыми ценами.

Уровни динамического ряда имеют свойство изменяться с различной скоростью и интенсивностью. Для характеристики развития явления во времени применяются специальные стати­стические показатели.

Показатели анализа ряда динамики могут рассчитываться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, — базисным.

Для расчета показателей на постоянной базе каждый уровень сравнивается с одним и тем же базисным уровнем. Рассчитанные при этом показатели называются базисными. Для расчета показа­телей на переменной базе каждый последующий уровень сравни­вается с предыдущим, а показатели называются цепными.

Таблица 29 Показатели рядов динамики

Показатели рядов динамики	Базисные	Цепные
Абсолютный прирост, ∆
Коэффициент роста,
Коэффициент прироста	1-	1-
Темп роста, Тр.
Темп прироста, Т пр.	Тр-100	Тр-100
Абсолютное значение 1 % прироста, А.

Для обобщения характеристики динамики исследуемого яв­ления за ряд периодов определяют различного рода средние по­казатели, среди которых можно выделить:

1.Средний уровень ряда:

а) интервальный равноотстоящий ряд – по средней арифметической простой;

б) интервальный неравноотстоящий ряд – по средней арифметической взвешенной;

в) моментный равноотстоящий ряд – по средней хронологической простой;

г) моментный неравноотстоящий ряд – по средней хронологический взвешенной;

2. Средний абсолютный прирост:

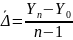
3. Средний темп роста: ,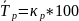

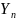–последний уровень ряда, первый уровень ряда.

4. Средний темп прироста:

Пример. Требуется провести анализ динамики продажи мясных консервов за 2003-2007 г.г. по следующим условным данным.

Таблица 30 Динамика продажи мясных консервов в одном из регионов за 2003-2007г.г. и расчет аналитических показателей динамики.

Годы	Консервы мясные млн. усл. банок (У)	Абсолютные приросты		Темп роста, %		Темп прироста, %		Абсолютное значение 1 % прироста, млн. усл. банок
		базис- ные	цеп- ные	базис- ные	цеп- ные	базис- ные	цеп- ные
2003	891	-	-	100,0	100,0	-	-	-
2004	806	-85	-85	90,5	90,5	-9,5	-9,5	8,91
2005	1595	+704	+789	179,0	197,9	+79,0	+97,9	8,06
2006	1637	+746	+42	183,7	102,6	+83,7	+2,6	15,95
2007	1651	+760	+14	185,3	100,9	+85,3	+0,9	16,37
Итого	6580	-	-	-	-	-	-	-

1. Средний уровень ряда: так как ряд динамики интервальный, равноотстоящий определяем уровень ряда по средней арифметической простой:

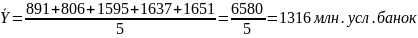
2. Средний абсолютный прирост: =

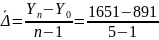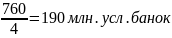
3. Средний темп роста:

,

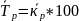
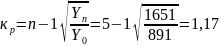
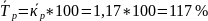2. Средний темп прироста:

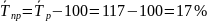
ИСХОДНЫЕ ДАННЫЕ

Годы	2006	2007	2008	2009	2010
Производство промышленной продукции, млн.руб.	68	72	68	75	84

Задачи для самостоятельного решения:

Задача 9.1 Имеются данные о розничной торговой сети района:

Таблица 31 Исходные данные

Год	Число работников фирмы
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
ххх1 ххх2 ххх3 ххх4 ххх5	100 120 150 160 180	240 210 250 220 180	50 40 32 38 52	110 130 150 170 190	80 90 120 130 150	70 60 50 65 70	42 40 46 50 52	45 55 70 80 100	80 90 100 120 80	150 170 190 200 220	130 140 190 150 170	210 220 240 250 240	180 190 160 150 200	240 250 260 290 280	150 160 170 195 210

Определить:

1. Вид ряда динамики?

2. Абсолютные приросты, темпы роста, темпы прироста, абсолютное значении 1% прироста? базисным и цепным способом. Полученные данные представьте в табличной форме.

3. Вычислите средние характеристики ряда динамики.

4. Сделайте выводы.

Задача 9.2 Заполните недостающие показатели:

Таблица 32 Исходные данные

Года	Товарная продукция (тыс.руб.)	Цепные показатели динамики
		D, тыс.	Тр.	Тпр.	А
ххх1	84,2	-	100,0	-	-
ххх2		2,8
ххх3			105,4
ххх4				5,8
ххх5				6,9
ххх6
ххх7			102,3		1,062
ххх8		3,2

Задание 2

Вопросы для самоконтроля:

1. Что такое динамический ряд?

2. В чем заключается разница между интервальным и моментным рядом динамики?

3. Как определить абсолютный прирост, темп роста, темп прироста, абсолютное значения 1% прироста и их среднее значения?

Литература: Егоров Л.И. «Статистика» стр.94-98,

Шмойлова Р.А. «Практикум по теории статистики» стр.234-280.

Домашнее задание: подготовиться к проверочному тесту по пройденному материалу.