Задание 1

Решите задачи.

На оценку «удовлетворительно» 7.1 (пункты а, б)

На оценку «хорошо» 7.1 (пункты а, б, в)

На оценку «отлично» 7.1 (пункты а, б, в, г)

Методические указания к проведению практической работы:

Различия индивидуальных значений признака внутри изу­чаемой совокупности называются вариацией признака. Она воз­никает в результате того, что индивидуальные значения призна­ка складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае.

Средняя величина — обобщающая характеристика признака изучаемой совокупности, но она не показывает строение сово­купности, не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредото­чены ли они вблизи или значительно отклоняются от нее. Если отдельные варианты недалеко отстоят от средней, то говорят, что данная средняя хорошо представляет изучаемую со­вокупность. Для изучения величины отклонений применяют по­казатели вариации.

При характеристике колеблемости признака применяют сис­тему абсолютных и относительных показателей.

К абсолютным показателям вариации относятся

1. Размах вариации:

,

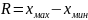где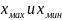 – максимальное и минимальное значение в ряду.

2. Среднее линейное отклонение

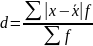, где 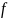- частота признака;

3. Дисперсия:

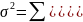
4. Среднее квадратичное отклонение:

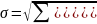
Эти показатели (кроме дисперсии) измеряются в тех же еди­ницах, что и сам признак: в тоннах, метрах, секундах, рублях. К относительным показателям вариации относятся:

1. Коэффициент осцилляции:

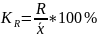
2. Линейный коэффициент вариации:

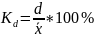
3. Коэффициент вариации:

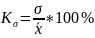
Пример Имеются выборочные данные о распределении учителей средних школ по стажу работы. Определить:

1. средний стаж работы учителей;

2. размах вариации;

3. среднее линейное отклонение;

4. дисперсию;

5. среднее квадратическое отклонение;

6. коэффициенты вариации

Таблица 25 – Распределение учителей средних школ по стажу работы

Группы учителей по стажу работы, лет, х	Число учителей в % к итогу , f
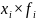
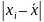
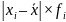
8 9 10 11 12	14 20 30 24 12	112 180 300 264 144	2 1 0 1 2	28 40 0 48 24	56 40 0 48 96
Итого	100	1000	-	140	240

Решение.

1. Средний стаж работы учителей; 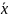= 1000/100 = = 10 лет

2. Размах вариации =12-8=4 года.

3. Среднее линейное отклонение

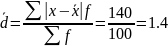
4. Дисперсия 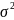= 240/100 = 2.4

5. Среднее квадратическое отклонение 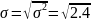=1.55

6. Коэффициент осцилляции: =

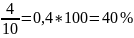
7. Линейный коэффициент вариации:

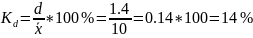
8. Коэффициент вариации:

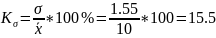
Совокупность недостаточно однородна, так как коэффициент осцилляции более 33%.

Для характеристики структуры совокупности применяются особые показатели, которые называют структурными средними. К таким показателям относятся мода и медиана. В отличие от средней арифметической и средней гармонической мода и ме­диана совпадают с конкретным числом, имеющимся в вариаци­онном ряду, и не всегда совпадают со средней арифметической и средней гармонической.

Модой {Мо) называется чаще всего встречающийся вариант, или то значение признака, которое соответствует максимальной точке теоретической кривой распределений.

В дискретном вариационном ряду мода — это варианта с наибольшей частотой.

4,4; 4,3; 4,4; 4,5; 4,3; 4,3;4,6; 4,2; 4,6;

Мо=4,3 тыс. руб.

4,2; 4,3; 4,3; 4,3; 4,4; 4,4; 4,5; 4,6 ; 4,6;

Ме= 4,4

Цена, руб.	Число торговых предприятий
52	12
53	48
54	56
55	60
56	14
Всего	190

Мо=55руб.

Ме=54руб.

Пример. При обследовании 500 семей рабочих одной из отраслей промышленности установлены следующие их размеры по количеству членов семей:

Таблица 26 Распределение семей по количеству их членов

Количество членов семьи, чел.	Число семей
2	50
3	80
4	260
5	40
6	30
7	20
8	10
9	10

Определите моду данного вариационного ряда распределения.

Решение. Модальной величиной в данном случае будет семья, в составе которой 4 человека, так как этому значению в нашем ряду распределения соответствует наибольшее число семей (260).

В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального ин­тервала, то есть того интервала, который имеет наибольшую час­тоту (частость). В пределах интервала надо найти то значение признака, которое является модой.