Практическая работа № 5-6

Тема: «Расчет относительных и средних величин»

Цель работы: углубить и закрепить теоретические знания по теме «Формы выражения статистических показателей», отработать навыки вычисления, научиться грамотно, характеризовать изучаемую совокупность соответствующими показателями.

После изучения темы студент должен:

Знать:

• технику расчета статистических показателей, характеризующих социально-экономические явления;

Уметь:

• выполнять расчеты статистических показателей и формулировать основные выводы;

Ключевые слова и термины.

Натуральные, стоимостные, трудовые величины, относительная величина динамики, ключевого задания, выполнения плана (реализация плана), относительная величина структуры, координации, интенсивности, сравнения, средняя величины, средняя арифметическая, средняя гармоническая, средняя хронологическая.

Программа работы:

Задачи 1

Решите задачи.

На оценку «удовлетворительно» 5.1 и 5.2, 6.1,6.2

На оценку «хорошо» 5.1; 5.2; 5.3; 5.4, 6.1, 6.2,6.3

На оценку «отлично» 5.1; 5.2; 5.3; 5.4; 5.5, 6.1, 6.2,6.3,6.4

Методические указания к проведению практической работы:

Абсолютные величины — исходная, первичная, самая общая форма выражения статистических показателей, характеризующая объем совокупности (то есть число единиц, ее составляющих). Абсолютные величины представляют собой суммарные числа, взятые из статистических таблиц без преобразования. Они непосредственно констатируют размеры общественных явлений в определенных условиях места и времени.

Различают два вида абсолютных величин: индивидуальные и суммарные.

Индивидуальные абсолютные величины характеризуют размеры признака у отдельных единиц совокупности (например, размеры заработной платы отдельного работника, вклада гражданина в определенном банке и т.д.). Они получаются непосредственно в процессе статистического наблюдения и фиксируются в первичных учетных документах.

В отличие от индивидуальных суммарные абсолютные величины характеризуют итоговую величину признака по определенной совокупности объектов, охваченных статистическим наблюдением. Они являются суммой количества единиц изучаемой совокупности {численность совокупности) или суммой значений варьирующего признака всех единиц совокупности (объем варьирующего признака). Например, численность торгово-оперативых работников магазина, сумма издержек обращения коммерческой фирмы и т.д.

Абсолютные статистические величины представляют собой именованные числа, то есть имеют какую-либо единицу измерения. Абсолютные статистические величины могут быть как положительными (доходы), так и отрицательными (убытки, потери).

В зависимости от сущности исследуемого социально-экономического явления абсолютные статистические величины выражаются в натуральных, стоимостных и трудовых единицах измерения.

Пример. За отчетный период предприятие произвело следующие виды мыла и моющих средств.

Таблица 9 Виды моющих средств

Виды мыла и моющих средств	Количество, кг
Мыло хозяйственное 60%-й жирности Мыло хозяйственное 40%-й жирности Мыло туалетное 80%-й жирности Стиральный порошок 10%-й жирности	500 250 1500 2500

Требуется определить общее количество выработанной предприятием продукции в условно-натуральных единицах измерения. За условную единицу измерения принимается мыло 40%-й жирности.

Решение. Для определения общего количества продукции, выработанной предприятием, необходимо исчислить коэффициенты перевода. Если условной единицей измерения становится мыло 40%-й жирности, то это значение жирности принимается равным единице. Тогда коэффициенты перевода в условное мыло (40%-й жирности) исчисляются так:

мыло хозяйственное 60%-й жирности: 60 : 40 = 1,5;

мыло туалетное 80%-й жирности: 80 : 40 = = 2,0;

стиральный порошок 10%-й жирности: 10 : 40 = 0,25.

Далее определим количество продукции в условно-натуральных единицах измерения.

Таблица 10 Общий объем производства мыла и моющих средств по видам

Виды мыла и мою­щих средств	Количе­ство, кг	Коэффи­циент перевода	Количество про­дукции в условно-натуральном исчислении, кг
Мыло хозяйственное 60%-й жирности Мыло хозяйственное 40%-й жирности Мыло туалетное 80%-й жирности Стиральный поро­шок 10%-й жирности	500 250 15002500	1,5 1,0 2,0 0,25	750 250 3000 625
Итого	4750	-	4625

Общий объем производства мыла и моющих средств в 40%-м исчислении составил 4625 кг.

Одна из важнейших форм обобщающих показателей в статистике — относительные величины. Они выражают меру количественных соотношений, присущих конкретным явлениям или статистическим объектам. При расчете относительной величины измеряется отношение двух взаимосвязанных величин (преимущественно абсолютных), что очень важно в статистическом анализе. Относительные величины широко используются в статистическом исследовании, позволяя провести сравнения различных показателей, и делают такое сравнение наглядным.

Относительные величины вычисляются как отношение двух чисел. При этом числитель называется сравниваемой величиной, а знаменатель — базой относительного сравнения. В зависимости от характера изучаемого явления и задач исследования базисная величина может принимать различные значения, что приводит к различным формам выражения относительных величин. Относи­тельные величины измеряются:

• в коэффициентах — если база сравнения принята за 1, то относительная величина выражается целым или дробным числом, показывающим, во сколько раз одна величина больше другой или какую часть ее составляет;

• в процентах, если база сравнения принимается за 100;

• в промилле, если база сравнения принимается за 1000;

• в продецимилле, если база сравнения принимается за 10 000;

• в именованных числах (км, кг, га) и др.

В каждом конкретном случае выбор той или иной формы относительной величины определяется задачами исследования и социально-экономической сущностью, мерой которого выступает искомый относительный показатель.

По своему содержанию относительные величины подразделяются на следующие виды:

• планового задания и выполнения плана;

• динамики;

• структуры;

• координации;

• интенсивности;

• сравнения.

Для решения задач используем следующие виды относительных величин:

1. Относительный показатель динамики:

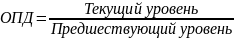
Пример Рассчитайте цепные (переменные) и базисные(постоянные) относительные величины динамики численности работников торгового предприятия за 2007-2010 гг.

Таблица 11 Динамика численности работников торгового предприятия за 2007-2010 гг.

Показатель	2007 г.	2008 г.	2009 г.	2010 г.
Численность работников, чел.	1285	1857	3345	3530

Решение: Рассчитаем ОПД для 2008 г.:

Базисный темп роста =1857/1285*100 % = 144,5 %.

Цепной темп роста =1857/1285*100 % = 144,5 %.

Рассчитаем ОПД для 2009 г.:

Базисный темп роста =3345/1285*100 % = 260,3 %.

Цепной темп роста =3345/1857* 100 % = 180,1 %.

Аналогичным образом рассчитываются показатели динамики для 2010г. Результаты расчетов занесем в таблицу12

Таблица 12 – Базисные и цепные относительные показатели динамики численности работников торгового предприятия

Год	Численность работников, чел.	ОПД (темп роста), %
		базисный. базисный	Цепной
2007 2008 2009 2010	1285 1857 3345 3530	100,0 144,5 260,3 274,7	100,0 144,5 180,1 105,5

Анализ данных таблица12 показал, что за период с 2007 по 2010 г. наблюдался постепенный рост численности работников торгового предприятия.

2. Относительный показатель плана (выполнения планового задания)

Пример В январе отчетного года валовой доход фирмы, занимающейся производством и продажей сложной бытовой техники, составил 1500 тыс. руб., в феврале планируется товарооборот в 1800 тыс. руб.

Определить относительную величину планового задания.

Решение: ОПП = 1800 /1500 *100% = 120 %.

Таким образом, в феврале планируется увеличение валового дохода фирмы на 20 %.

3. Относительный показатель реализации плана (% выполнения плана)

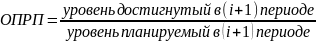
Пример Валовой доход фирмы, занимающейся производством и продажей сложной, бытовой техники, в феврале отчетного года составил 2055,5 тыс. руб. при плане 1800 тыс. руб. Определить степень выполнения плана по валовому доходу фирмы в феврале текущего года.

Решение: ОПРП= 2055,5/1800*100=114,2%

План по валовому доходу в феврале текущего года фирмой выполнен на 114,2%, то есть перевыполнение плана составило 14,2%.

4. Относительный показатель структуры.

Пример. Имеются следующие данные о розничном товарообороте предприятия за 2009-2010 гг., млн. руб.:

Таблица 13 –Динамика розничного товарооборота предприятия по кварталам 2009-2010 гг.

Год	I квартал	IIквартал квартал	IIIквартал квартал	IVквартал квартал	Всего за год
2009 2010	173,7 200,7	182,4 205,9	190,3 215,1	206,9 240,9	753,3 862,6

Исчислить относительные величины структуры розничного товарооборота предприятия по кварталам за каждый год.

Решение: Исчислим относительные величины структуры розничного товарооборота за 2009 и 2010 гг.

d =173, 7 /753, 3*100 % = 23, 0 %; d =182, 4/753, 3*100% = 23, 3 %

d = 190, 3 /753, 3*100%=24, 2%; d=206, 9/753, 3*100%=23, 9%

Исчисленные относительные величины структуры товаро­оборота представлены в таблице14.

Таблица 14–Структура розничного товарооборота предприятия по кварталам 2009-2010гг.

Квартал	Удельный вес розничного товарооборота, %
	2009г. 2003 г.	2010 г.
I II III IV	23,0 24,2 25,3 27,5	23,3 23,9 24,9 27,9
. Итого	100,0	100,0

Данные таблицы 14 свидетельствуют о том, что в изучаемые годы удельный вес розничного товарооборота закономерно растет от I к IV кварталу.

Средняя величина в статистике — обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени. В статистике применяются различные виды средних величин:

1. Средняя арифметическая простая:

Пример Имеется информация о стаже пяти рабочих, при этом стаж первого рабочего составил 5 лет, второго — 7, третьего — 4, четвертого — 10, пятого — 12 лет. Определить средний стаж работы.

Решение: Поскольку в исходных данных значение каждого варианта встречалось только один раз, для определения среднего стажа одного рабочего следует применить формулу простой средней арифметической. В нашем примере средний стаж будет равен:

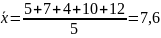
2. Средняя арифметическая взвешенная:

Пример Рассчитать среднюю заработную плату работников в бригаде из 20 человек, оплата труда которых варьируется от 10800 до 14400 руб., где х–варианты осредняемого признака, f – частота, показывающая, сколько раз встречается i-е значение в совокупности (таблица15).

Таблица 15– Исходные данные

Заработная плата работников, х	10800	13200	13600	14000	14400	Итого
Число работников, f	2	11	5	1	1	20

Решение: применяя формулу средней арифметической взвешенной, получаем:

Задача. Определить средний возраст управленческого персонала последующим исходным данным.

Возраст, лет	Среднее значение интервала	Число менеджеров
До 25	(20+25)/2=22,5	7
25-30	(25+30)/2=27,5	13
30-40	(30+40)/2=35	38
40-50	(40+50)/2=45	42
50-60	(50+60)/2=55	16
60 и более	(60+70)/2=65	5
Итого	-	121

=41год

3. Средняя гармоническая взвешенная:

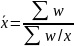
Пример. Рассчитать среднюю заработную плату по трем предприятиям по следующим исходным данным.

Таблица 16– Исходные данные

Предприятия	Месячный фонд заработной платы, тыс.руб.	Средняя заработная плата, руб.
1	5648,4	10460
2	3327,5	12100
3	5175,4	11300
Итого	14151,3	?

Решение: Определяем исходное соотношение средней для показателя «Средняя заработная плата»

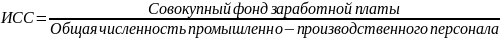
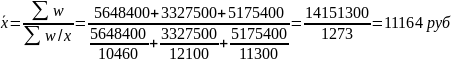
4.Средняя хронологическая простая:

Пример. Известны товарные остатки магазина на 1 –е число каждого месяца (тыс. руб.): на 1.01. на 1.02. на 1.03. на 1.04.

18 14 16 20

Определить среднемесячный товарный остаток за 1 квартал.