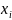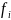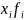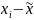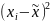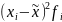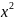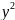- •Статистика
- •Содержание:
- •1 Общие сведения
- •Методические указания для выполнения практических работ практическая работа №1
- •Задание 1:
- •Практическая работа № 5-6
- •Задачи 1
- •5. Средняя хронологическая взвешенная:
- •Задача 5.5 На основании данных таблицы Определите недостающие показатели. Укажите виды относительных величин. Сделайте выводы.
- •Задание 1
- •Конкретное значение моды для интервального ряда определяется формулой:
- •– Нижняя граница модального интервала;
- •– Нижняя граница медианного интервала;
- •Практическая работа № 10
- •Практическая № 11 Тема: «Применение показателей рядов динамики и модели сезонных колебаний в комплексном анализе социально-экономических явлений и процессов»
- •По данным таблицы вычислим усредненные значения уровней по одноименным периодам способом средней арифметической простой:
- •Практическая работа № 12-13
- •Задание 1
Задание 1
Решите задачи:
На оценку «удовлетворительно» 14.1,
На оценку «хорошо» 14.1, 14.2, 14.3,
На оценку «отлично» 14.1, 14.2, 14.3, 14.4.
Методические указания к проведению практической работы:
Выборочное наблюдение — один из наиболее широко применяемых видов несплошного наблюдения. При его проведении обследуются не все единицы изучаемого объекта (генеральной совокупности), а лишь некоторые, отобранные определенным способом часть этих единиц (выборочная совокупность). Цель выборочного наблюдения — определение параметров генеральной совокупности на основе параметров выборочной совокупности. Разница между генеральными и выборочными параметрами называется ошибкой выборки или ошибкой репрезентативности. Выделяют следующие этапы проведения выборочного наблюдения:
определение необходимого объема выборки и способа отбора;
проведение отбора;
обобщение данных наблюдения и расчет выборочных характеристик;
расчет ошибок выборки;
распространение выборочных характеристик на генеральную совокупность.
Основные характеристики параметров генеральной и выборочной совокупностей обозначаются следующими символами:
N — генеральная совокупность (подлежащая измерению статистическая совокупность, из которой производится отбор части единиц);
п — выборочная совокупность (выборка) (отобранная из генеральной совокупности часть единиц, которая подлежит непосредственному изучению);
— генеральная средняя (среднее значение признака в генеральной совокупности);
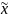 — выборочная
средняя;
— выборочная
средняя;
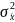 —
генеральная
дисперсия;
—
генеральная
дисперсия;
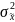 —выборочная
дисперсия;
—выборочная
дисперсия;
р — генеральная доля;
w — выборочная доля
Для решения задач следующие формулы:
1.
Средняя ошибка повторной выборки:
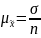
2. Средняя ошибка бесповторной выборки:
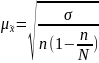
3
Предельная ошибка выборки:

где t – коэффициент доверия, определяемый в зависимости от уровня вероятности.
вероятность |
0,683 |
0,866 |
0,954 |
0,988 |
0,997 |
0,999 |
t |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4.
Границы генеральной совокупности:

Пример. В городе проживает 250 тыс.семей. Для определения среднего числа детей в семье была организована 2-% случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
Таблица 51 Исходные данные
Число детей в семье |
0 |
1 |
2 |
3 |
4 |
5 |
Количество семей |
1000 |
2000 |
1200 |
400 |
200 |
200 |
С вероятностью 0,954 найдите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение: В начале на основе имеющегося распределения семей определим выборочную среднюю и дисперсию для этого проведем расчеты во вспомогательной таблице.
Таблица 52 Вспомогательная таблица
Число
детей в семье, |
Количество
семей, |
|
|
|
|
0 |
1000 |
0 |
-1,5 |
2,25 |
2250 |
1 |
2000 |
2000 |
-0,5 |
0,25 |
500 |
2 |
1200 |
2400 |
0,5 |
0,25 |
300 |
3 |
400 |
1200 |
1,5 |
2,25 |
900 |
4 |
200 |
800 |
2,5 |
6,25 |
1250 |
5 |
200 |
1000 |
3,5 |
12,25 |
2450 |
Итого |
5000 |
7400 |
- |
- |
7650 |
Выборочная
средняя

Дисперсия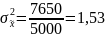
Вычислим
теперь предельную ошибку выборки ( с
учетом того, что р=0,954, t=2)
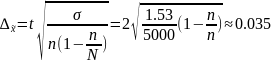
Следовательно, пределы генеральной средней:
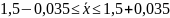
Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходятся три ребенка.
4 Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки.
Объем выборки при случайной и механической выборке:
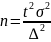 (повторный
отбор)
(повторный
отбор)
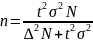 (бесповторный
отбор)
(бесповторный
отбор)
Пример. В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225
Решение: Рассчитаем необходимый объем выборки:
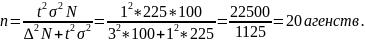
Задачи для самостоятельного решения.
Задача 14.1
В порядке механической выборки обследован возраст 100 студентов вуза из общего числа 2000 человек. Результаты обработки материалов наблюдения приведены в таблице:
Таблица 53 Исходные данные
Возраст, лет |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
Число студентов, чел. |
11 |
13 |
18 |
23 |
17 |
10 |
8 |
Установите: а) средний возраст студентов вуза по выборке; б) величину ошибки при определении возраста студентов на основе выборки; в) вероятные пределы колебания возраста для всех студентов при вероятности 0,997.
Задача14.2 В микрорайоне проживает 5000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что выборочной средней не должна превышать 0,8 человека с вероятностью Р==0,954 (t=2) и при среднем, квадратическом отклонении 3 человека
Задача 14.3 На склад магазина поступило 100 ящиков товара А по 80 шт. в каждом. Для установления среднего веса товара следует провести серийную выборку товара методом механического отбора так, чтобы с вероятностью 0,954 ошибка выборки, не превышала 2 г. Дисперсия серийной выборки 4 (на основе предыдущих обследований). Определить необходимый объем выборки.
Задача 14.4 На складе магазина находятся 200 ящиков с товаром А по 40 шт. в каждом ящике. Для проверки качества этого товара было произведено 10%-я серийная выборка. В результате выборки установлено, что доля бракованных изделий составляет10%. С вероятностью 0,997 определить пределы, в которых находится доля бракованных изделий в партии.
Задание 2
Вопросы для самоконтроля:
Что такое выборочное наблюдение?
Что такое генеральная и выборочная совокупность?
Каким бывают ошибки выборки?
Литература:
Егоров Л.И. «Статистика» стр.115-128,
Шмойлова Р.А. «Практикум по теории статистики» стр.169-187.
Домашнее задание: подготовиться к проверочному тесту по пройденному материалу.
Практическая работа № 15
Тема: «Корреляционно-регрессионный анализ с применением средств вычислительной техники (программа Excel)»
Цель работы: углубить и закрепить теоретические знания по теме «Статистическое изучение взаимосвязей», уметь выявить связи между явлениями.
После изучения темы студент должен:
Знать: технику расчета статистических показателей, характеризующих социально-экономические явления;
Уметь: осуществлять комплексный анализ изучаемых социально-экономических явлений и процессов с использованием средств вычислительной техники;
Ключевые слова и термины: корреляционная связь, поле корреляции, эмпирические линии связи, линейный коэффициент корреляции, уравнение регрессии, корреляционно-регрессивные модели.
Программа работы:
Задание 1
Решите задачи:
На оценку «удовлетворительно» 15.1
На оценку «хорошо 15.1 и 15.2(частично);
На оценку «отлично 15.1; 15.2; (полностью);
Методические указания к проведению практической работы:
Различают два типа связей между различными явлениями и их признаками: функциональную или жестко детерминированную, с одной стороны, и статистическую или стохастически детерминированную- с другой.
Если с изменением значения одной из переменных вторая изменяется строго определенным образом, т.е. значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональной. Стохастически детерминированная связь не имеет ограничений и условий, присущих функциональной связи. при статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной. Корреляционной связью называют важнейший частный случай статистической связи, состоящий в том, что разным значениям одной переменной соответствуют различные средние значения другой. С изменением значения признака х закономерным образом изменяется среднее значение признака у; в то время как в каждом отдельном случае значение признака у (с различными вероятностями) может принимать множество различных значений.
Для выявления наличия связи, ее характера и направления в статистике используются следующие методы: приведения параллельных данных, аналитических группировок, графический, корреляции. Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере. Сравним изменение двух величин:
Таблица 54 Исходные данные
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
У |
5 |
9 |
6 |
10 |
14 |
17 |
15 |
20 |
23 |
Видно, что с увеличением величины Х величина У также возрастает. Можно сделать предположение, что связь между ними прямая и что ее можно описать уравнение прямой или уравнением параболы второго порядка.
Корреляционный анализ изучает взаимосвязи показателей и позволяет решить следующие задачи:
1.Оценка тесноты связи между показателями с помощью парных, частных и множественных коэффициентов корреляции.
2. Оценка уравнения регрессии.
Парная регрессия характеризует связь между двумя признаками : результативным и факторным. Аналитически связь между ними описывается уравнениями:
прямой
–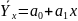 ;
;
гиперболы
–
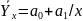 ;
;
параболы
–
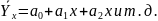 ;
;
Определить тип уравнения можно следующим образом:
Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи гиперболическая. Если факторный признак увеличивается в арифметической прогрессии, а результативный значительно быстрее, то используется параболическая связь.
Оценка параметров уравнения регрессии осуществляется методом наименьших квадратов.
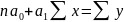

Теснота корреляционной связи может быть определена с помощью линейного коэффициента корреляции, который определяется по формуле:

Линейного коэффициента корреляции изменяется в пределах -1 ≤ τ ≤1
если «+», то связь прямая,
если « - », то обратная связь,
если «0» ,то связи нет.
Пример Зависимость между затратами на 1 рубль произведенной продукции и прибылью за 2010 г. характеризуется следующими данными:
Таблица 55 Исходные данные
№ предприятия
|
затраты на 1 рубль произведенной продукции, коп, х |
Прибыль до тыс. руб., y |
1 |
77 |
1070 |
2 |
77 |
1001 |
3 |
81 |
789 |
4 |
82 |
779 |
5 |
89 |
606 |
6 |
96 |
221 |
Итого |
502 |
4466 |
Определите вид корреляционной зависимости, постройте уравнение регрессии, рассчитайте параметры уравнения, вычислите тесноту связи. Объясните полученные статистические характеристики.
Решение: рассчитаем вспомогательную таблицу
Таблица 56 Расчет сумм для определения параметров парного линейного уравнения регрессии
№ предприятия
|
затраты на 1 рубль произведенной продукции, коп, х |
Прибыль до тыс. руб., y |
|
х*у |
|
|
1 |
77 |
1070 |
5929 |
82390 |
1144900 |
1012,86 |
2 |
77 |
1001 |
5929 |
77077 |
1002001 |
1012,86 |
3 |
81 |
789 |
6561 |
63909 |
622521 |
851,75 |
4 |
82 |
779 |
6724 |
63888 |
606841 |
801,47 |
5 |
89 |
606 |
7921 |
53934 |
367236 |
529,51 |
6 |
96 |
221 |
9216 |
21216 |
48841 |
247,55 |
Итого |
502 |
4466 |
42280 |
362404 |
3792340 |
4466,00 |
Система нормальных уравнений для данного примера имеет вид:
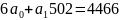
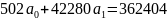
6*502
+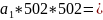 4466*502
4466*502
502*6
+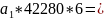 362404*6
362404*6
3012 + *252004=2241932
3012 +253680 =2174424
-1676 =67508
= -40.28
6 - 40.28*502=4466
Отсюда:
Следовательн,
Зависимость обратная.
Теснота
связи определяется по формуле:
Связь обратная и тесная
Задачи для самостоятельного решения.
Задача 15.1 Используем метод приведения параллельных данных, установите направление и характер связи между двумя признаками:
Таблица 57 Исходные данные
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Средняя зарплата руб. |
9080 |
9630 |
8040 |
8490 |
9970 |
9900 |
8770 |
8690 |
9570 |
9520 |
Прожиточный минимум на душу населения руб. |
4490 |
4490 |
4460 |
4520 |
4380 |
4330 |
4340 |
4340 |
4330 |
4280 |
Задача 15. 2Требуется исследовать связь между выработкой товарной продукции на одного работающего и стоимость основных производственных фондов шести предприятий города.
Таблица 58 Исходные данные
1. Выработка товарной продукции на одного работника в тыс. руб. |
Предприятия
|
|||||||
Варианты |
1 |
2 |
3 |
4 |
5 |
6 |
||
1 |
16 |
4,0 |
6,0 |
5,5 |
7,0 |
8,0 |
8,5 |
|
2 |
17 |
2,3 |
2,8 |
3,2 |
3,0 |
4,3 |
4,5 |
|
3 |
18 |
5,0 |
7,0 |
7,5 |
8,0 |
7,5 |
9,5 |
|
4 |
19 |
12,0 |
15,0 |
12,8 |
13,8 |
16,8 |
18,0 |
|
5 |
20 |
15,0 |
16,0 |
18,0 |
20,0 |
22,0 |
21,0 |
|
6 |
21 |
4,5 |
4,8 |
5,1 |
5,0 |
5,6 |
5,8 |
|
7 |
22 |
4,3 |
4,5 |
4,8 |
5,2 |
5,0 |
5,6 |
|
8 |
23 |
5,8 |
6,0 |
6,4 |
6,8 |
6,5 |
6,9 |
|
9 |
24 |
7,0 |
7,4 |
7,8 |
7,5 |
7,8 |
8,0 |
|
10 |
25 |
6,2 |
6,8 |
7,2 |
7,4 |
7,8 |
8,0 |
|
11 |
26 |
5,1 |
5,4 |
5,8 |
6,2 |
6,6 |
7,0 |
|
12 |
27 |
5,9 |
6,5 |
7,0 |
7,5 |
7,3 |
7,8 |
|
13 |
28 |
11,0 |
12,0 |
13,0 |
14,0 |
15,0 |
16,0 |
|
14 |
29 |
8,2 |
8,6 |
9,0 |
9,4 |
9,8 |
10,0 |
|
15 |
30 |
3,2 |
3,5 |
3,8 |
4,1 |
4,4 |
4,7 |
|
2.Стоимость основных производственных фондов в тыс. руб. |
Предприятия |
|||||||
Варианты |
1 |
2 |
3 |
4 |
5 |
6 |
||
1 |
16 |
0,5 |
1,5 |
2,5 |
3,5 |
4,5 |
5,5 |
|
2 |
17 |
0,7 |
0,9 |
1,2 |
1,5 |
1,8 |
2,0 |
|
3 |
18 |
1,2 |
1,5 |
1,8 |
2,0 |
2,3 |
2,5 |
|
4 |
19 |
2,4 |
2,8 |
3,2 |
3,8 |
4,0 |
4,3 |
|
5 |
20 |
5,0 |
5,2 |
5,4 |
5,6 |
5,8 |
6,0 |
|
6 |
21 |
0,6 |
0,9 |
1,2 |
1,5 |
1,8 |
2,0 |
|
7 |
22 |
0,8 |
1,2 |
1,6 |
2,0 |
2,4 |
2,8 |
|
8 |
23 |
0,9 |
1,3 |
1,8 |
2,2 |
2,6 |
2,8 |
|
9 |
24 |
1,1 |
1,5 |
1,9 |
2,4 |
2,8 |
3,0 |
|
10 |
25 |
1,3 |
1,6 |
1,8 |
2,0 |
2,2 |
2,4 |
|
11 |
26 |
1,5 |
1,8 |
2,0 |
2,4 |
2,8 |
3,2 |
|
12 |
27 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
|
13 |
28 |
2,8 |
3,2 |
3,6 |
3,8 |
4,2 |
4,6 |
|
14 |
29 |
3,1 |
3,5 |
3,4 |
4,3 |
4,7 |
5,1 |
|
15 |
30 |
0,8 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
|
Задание 2
Вопросы для самоконтроля:
Какие виды связей существуют между явлениями?
Какие существуют методы выявления наличия корреляционной связи между двумя признаками?
Какие показатели измерения тесноты корреляционной связи между двумя признаками существуют?
Что такое уравнение регрессии? Какие существуют виды?
Что такое корреляционно-регрессивные модели?
Литература: Егоров Л.И. «Статистика» стр.131-132,
Шмойлова Р.А. «Практикум по теории статистики» стр.187-234.
Домашнее задание: подготовиться к проверочному тесту по пройденному материалу.
Литература
Громыко Г.Л. Теория статистики. – М., Практикум, 2001.
Гусаров В.М. Статистика. – М., 2001.
Егоров А.И. Статистика – СПБ., 1998.
Елисеева И.И., Избашев М.М. ''Общая теория статистики'' – М., Финансы и статистика, 2005
Ефимова М.Р., Рябцев В.М. ''Общая теория статистики'' – М., ИНФРА, 1996.
11. Сборник задач по теории статистики. Учебное пособие. Под редакцией Шмойловой Р.А., - М., Финансы и статистика, 2000
12. Теория статистики/ под редакцией профессора Шмойловой Р.А., - М. Финансы и статистика, 2000
13. Теория статистики/ Под редакцией Громыко Г.Л. – М., 2000.