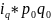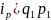Практическая работа № 12-13

Тема: «Расчет индексов и их применение в факторном анализе»

Цель работы: Закрепить теоретические знания по теме «Статистические индексы», научится строить и вычислять индексы, с помощью которых проводить анализ изучаемых явлений.

После изучения темы студент должен:

Знать: - технику расчета статистических показателей, характеризующих социально-экономические явления;

Уметь: - осуществлять комплексный анализ изучаемых социально-экономических явлений и процессов с использованием средств вычислительной техники

Ключевые слова и термины:

индекс, индексированные величины, индивидуальный индекс, вес индекса, агрегатный индекс, индекс в форме средней арифметической , индекс в форме средней гармонической, индекс постоянного, переменного состава, структурный индекс;

Программа работы.

Задание 1

Решите задачи:

На оценку «удовлетворительно» 12.1

На оценку «хорошо» 12.1; 12.2; 12.3

На оценку «отлично» 12.1; 12.2; 12.3,12.4,12,

Методические указания к проведению практической работы:

Индексы — относительные показатели, предназначенные для описания изменения величины какого-либо явления во времени, пространстве или по сравнению с любым эталоном. Индексы могут использоваться не только для сопоставления уровней явлений, но и для установления значимости причин, вызывающих их изменение.

Основной элемент индексного соотношения — индексируемая величина, которая представляет собой значение признака статистической совокупности, изменение которой является объектом изучения.

С помощью индексов решаются следующие основные задачи:

1) характеризуется общее изменение сложных социально - экономических явлений и отдельных его элементов (изучается развитие национальной экономики в целом и ее отдельных отраслей, определяется уровень жизни населения и т.д.);

2. выясняется роль отдельных факторов в формировании важнейших экономических показателей;

3. являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией — сравнение в пространстве, а также с планами, нормативами, прогнозами и т. д.;

4. используются в международных сопоставлениях макроэкономических показателей, то есть производится пересчет значений показателей из фактических цен в сопоставимые.

Для удобства применения индексного метода, составления формул индексов и их использования в экономико-статистическом анализе в теории статистики разработана определенная символика. Каждая индексируемая величина имеет условное обозначение:

i— индивидуальный индекс,

I — общий (агрегатный) индекс,

p— цена за единицу продукции,

q — количество продукции одного вида в натуральном выражении,

p q — товарооборот, стоимость продукции,

Знак внизу справа означает период: 0 — базисный, 1 — отчетный

Для решения задач используем следующие формулы:

1.Индивидуальный индекс цены: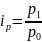

где 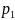– цена товара в текущем периоде;

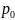– цена товара в базисном периоде;

2. Индивидуальный индекс физического объема: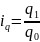

где 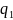– физический объем в текущем периоде;

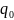– физический объем в базисном периоде;

3. Индивидуальный индекс товарооборота:

где 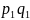– товарооборот в текущем периоде;

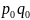– товарооборот в базисном периоде;

Проверка: ( в коэффициентах)

Пример. Рассмотрим подробнее индивидуальные индек­сы с учетом условных данных о ценах и реализации продукции за два периода:

Таблица 42 Исходные данные

Товар	Еди­ница изме­рения	III квартал		IV квартал
		Цена за 1 ед., руб.	Количе­ство	Цена за 1 ед., руб.	Количество
Молоко Яйцо Картофель	л шт. кг	19,8 36,7 6,8	7500 1690 14750	20,1 37,0 6,2	6800 1830 10050

При определении по данным таблицы статистических индексов III квартал принимается за базисный период, в котором цена единицы товара обозначается р₀, а количество —

IV квартал принимается за текущий или отчетный период, в котором цена единицы товара обозначается , а количество —

Тогда индивидуальные индексы составят:

цен

по молоку

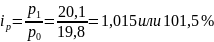
по яйцам

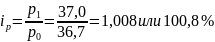
по картофелю

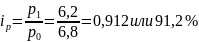
В 4 квартале цены на молоко и по яйца увеличились соответственно на1,5% и 0,8%, на картофель цены снизились на 8,8%.

физического объема

по молоку

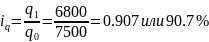
по яйцам

по картофелю

Физический объем реализации снизился по молоку на 9,3%, по картофелю на 31,9%.Физический объем реализации яиц увеличился на 8,3%.

товарооборота

по молоку

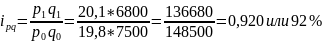
по яйцам 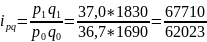=1,092или 109,2%

по картофелю

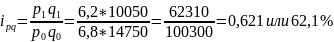
Товарооборот по представленным товаром увеличился по яйцам на 9,2%, по молоку и картофелю снизился на 8,0% и 37,9% соответственно.

В связи с тем, что индивидуальные индексы являются разновеликими по направлению и интенсивности изменения, возникает необходимость их обобщения при определении общего для данного ассортимента изменения цен и количества реализованных товаров. Для этого вычисляются соответствующие общие (сводные) индексы.

4. Сводный индекс товарооборота:

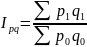
где -товарооборот в текущем периоде;

– товарооборот в базисном периоде;

5. Сводный индекс цены:

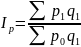
6. Сводный индекс физического объема:

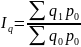
7. Проверка

= *

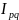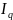
Пример. Имеются следующие данные о реализации плодово-ягодной продукции в области

Таблица 43 Исходные данные

Наименование товара	Июль		Август			Расчетные графы
	Цена за 1 кг в руб. ро	Продано, тн qо		Цена за 1 кг в руб.	Продано, тн
черешня	12	18		12	15		216	180	180
персики	11	22		10	27		242	270	297
виноград	9	20		7	24		180	168	216
Итого	x	х		Х	х		638	618	693

Рассчитать сводные индексы цены, физического объема и товарооборота.

Решение: Сводный индекс цены:

По данной товарной группе цены в августе по сравнению с июлем в среднем снизились на 10,8%.

Сводный индекс физического объема:

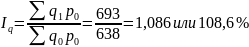
Физический объем реализации увеличился на 8,6%.

Сводный индекс товарооборота:

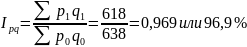
Товарооборот по данной товарной группе в текущем периоде по сравнению с базисным уменьшился на 3,1%

Проверка: 0,892*1,086=0,969

Таблица 43 Исходные данные

Наименование товара	Август		Сентябрь			Расчетные графы
	Цена за 1 кг в руб. ро	Продано, тн qо		Цена за 1 кг в руб.	Продано, тн
Товар А	10,0	12,0		15	12
Товар Б	8,0	7,0		10	13
Товар В	14,0	15,0		17	15
Итого

Помимо записи общих индексов в агрегатном виде в практике статистики часто используют формулы их расчета как величин, средних из соответствующих индивидуальных индексов.

Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. Помимо агрегатных индексов в статистике применяется другая их форма – средневзвешенные индексы. К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если отсутствуют данные о ценах, но имеется информация о стоимости продукции в текущем периоде и известны индивидуальные индексы цен по каждому товару, то нельзя определить общий индекс цен как агрегатный, но возможно исчислить его как средний из индивидуальных. Точно также, если не известны количества произведенных отдельных видов продукции, но известны индивидуальные индексы и стоимость продукции базисного года, можно определить общий индекс физического объема продукции как средневзвешенную величину.

Средний арифметический индекс тождествен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Только в этом случае величина индекса, рассчитанного по формуле средней арифметической, будет равна агрегатному индексу.

Средний арифметический индекс физического объема продукции вычисляется по формуле:

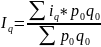
 где – индивидуальный индекс количества;

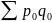– товарооборот в базисном периоде.

Пример .Имеются следующие данные о реализации молочных продуктов на городском рынке. Рассчитать сводный индекс физического объема

Таблица 44 Данные о реализации молочных продуктов на городском рынке

Товар	Реализация в базисном периоде, руб.,	Изменение физического объема реализации в текущем периоде по сравнению с базисным, % ( *100% - 100%),	Расчетные графы
молоко	46000	-6,4	0.936	43056
сметана	27000	-8,2	0.918	24786
творог	51000	+1,3	1.013	51663
Итого	124000	Х	Х	119505

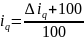
Рассчитать средний арифметический индекс:

Решение:

Физический объем реализации данных товаров в среднем снизился на 3,6%

Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса.

Средний гармонический индекс цены вычисляется по формуле:

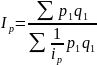
 где 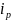– индивидуальный индекс цены;

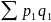– – товарооборот в текущем периоде;

Пример. По данным таблицы получите сводную оценку изменения цен.

Таблица 45Реализация овощной продукции

Товар	Реализация в текущем периоде, руб.,	Изменение цен объема в текущем периоде по сравнению с базисным, %( *100% - 100%)	Расчетные графы
морковь	23000	+4,0	1.04	23920
свекла	21000	+2,3	1.023	21483
лук	29000	-0,8	0.992	28768
Итого	73000	Х	Х	74171

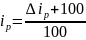
Решение:

Вычислим средний гармонический индекс цены.

Цены по данной товарной группе в текущем периоде по сравнению с базисным в среднем снизилась на 2,0 %.

Индекс цен переменного состава:

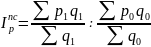
Индекс структурных сдвигов:

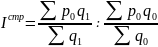
Индекс фиксированного состава:

Проверка

Задача: Провести анализ цен реализации товара в двух регионах по следующим данным:

Таблица 43 Исходные данные

Регион	Июнь		Июль			Расчетные графы
	Цена за 1 кг в руб. ро	Продано, шт. qо		Цена за 1 кг в руб.	Продано, шт.
1	12	10000		13	18000
2	17	20000		19	9000
Итого

Задачи для самостоятельного решения.

Задача 12.1 Имеются данные о ценах и количестве проданной моркови на рынке:

Таблица 46 Исходные данные

Месяц	Июль	Август	Сентябрь
Цена за 1 кг, руб	5,0	5,2	5,8
Количество, т	4,5	4,8	4,0

Определите:

- индивидуальные индексы цен ценным методом;

- индивидуальные индексы количества базисным методом;

- сделайте выводы.

Задача 12.2 Заполните недостающие показатели:

Таблица 47 Исходные данные

Месяц	Цена за 1 шт в руб	Индивидуальные индексы в %
		Цепные	Базисные
Июль		-	100,0
Август	120.0
Сентябрь		101,2	103,5
Октябрь			103,2
Ноябрь		108,4
Декабрь	125,6

Задача 12.3 Имеются данные по магазину овощи:

Таблица 48 Исходные данные

Варианты			Наименование товара		III квартал				IV квартал
					Цена за 1кг, руб		Количество кг.		Цена за 1кг, руб		Количество кг.
1	16	капуста картофель свекла		5,0 6,2 7,4		1020 1140 1280		5,2 6,4 7,0		1050 950 1120
2	17	капуста картофель свекла		4,8 6,3 7,1		980 540 680		5,3 7,2 6,8		780 620 720
3	18	капуста картофель свекла		5,3 6,2 7,0		1540 1320 1410		5,5 6,0 7,2		1480 1320 1210
4	19	капуста картофель свекла		5,2 5,0 7,0		990 840 720		5,1 6,2 7,0		920 940 650
5	20	капуста картофель свекла		4,5 5,2 6,2		780 750 680		4,4 5,0 6,5		720 700 710
6	21	капуста картофель свекла		4,6 6,0 7,2		610 580 680		4,4 6,2 7,4		740 620 650
7	22	капуста картофель свекла		4,7 5,4 5,5		1050 1240 1080		4,9 5,6 5,2		1120 1080 1540
8	23	капуста картофель свекла		4,8 6,2 7,0		950 1020 1140		5,0 6,0 7,2		920 1150 1240
9	24	капуста картофель свекла		4,3 6,1 6,5		640 680 1050		4,6 6,8 6,2		610 720 1240
10	25	капуста картофель свекла		4,6 5,8 6,0		980 950 640		5,2 5,0 5,8		910 1020 710
11	26	капуста картофель свекла		5,4 5,9 6,8		750 780 920		5,5 5,4 6,4		800 840 900
12	27	капуста картофель свекла		5,9 5,8 7,0		1410 1680 1230		5,6 6,0 7,2		1540 1310 1120
13	28	капуста картофель свекла		5,7 5,0 6,8		2480 2120 2540		5,9 5,2 7,4		2210 2480 2320
14	29	капуста картофель свекла		5,4 7,2 6,5		2310 2840 2000		5,5 7,0 6,8		2840 2140 2200
15	30	капуста картофель свекла		5,8 5,0 6,2		2420 2340 2710		6,0 5,2 6,4		2310 2840 2220

Определить общий индекс цены, общий индекс количества, общий индекс оборота розничной торговли, изменения оборота под влиянием цены и количества проданных товаров. Сделайте выводы

Задача 12.4 Имеются следующие данные о реализации товаров:

Таблица 49 Исходные данные

Товарные группы	Продано в базисном году в тыс.руб.	Изменения количества проданных товаров в текущем году по сравнению с базисным в %
А Б В	400 450 620	-8,0 +2,5 +3,2

Вычислить общий индекс физического объема товарооборота.

Задача 12.5 Имеются следующие данные о реализации товаров:

Таблица 50 Исходные данные

Товарные группы	Продано на сумму тыс.руб.		Изменения цен в отчетном периоде по сравнению с базисным в %
	базисным период	Отчетный период
Шерстяная ткань Одежда Обувь	520 480 720	620 540 780	+5,3 -2,4 +6,8

Вычислить:

1. Общий индекс товарооборота.

2. Общий индекс цен.

3. Общий индекс физического объема.

4. Абсолютную сумму перерасхода от изменения цен.

5. Докажите наличие взаимосвязи между общими индексами цен стоимости и физического объема.

Задание 2.

Вопросы для самоконтроля:

1. Что такое индекс?

2. Чем отличаются и что общего между индивидуальным и общим индексом?

1. Какая взаимосвязь существует между агрегатными индексами стоимости, физического объема и цены?

Литература:

Егоров Л.И. «Статистика» стр103-104.

Шмойлова Р.А. «Практикум по теории статистики» стр.300-384.

Домашнее задание: подготовиться к проверочному тесту по пройденному материалу.

Практическая работа № 14

Тема : «Расчет показателей выборки»

Цель работы: углубить и закрепить теоретические знания по теме «Методы выборочного наблюдения», уметь определять объёмы выборки, ошибки выборочного наблюдения, пределы генеральной совокупности.

После изучения темы студент должен:

Знать: технику расчета статистических показателей, характеризующих социально-экономические явления;

Уметь: - выполнять расчеты статистических показателей и формулировать основные выводы;

Ключевые слова и термины: выборочное наблюдение, выборочная совокупность, генеральная совокупность, повторная выборка, бесповторная выборка, ошибки выборочного наблюдения.

Программа работы