1.1.7 Эквивалентная схема транзистора с ок

Выражение для входного сопротивления биполярного транзистора, включенного по схеме с общим коллектором (эмиттерный повторитель)

На рисунке 1.11, б приведена эквивалентная схема замещения для эмиттерного повторителя.

 

1.1.8 Транзистор как активный четырехполюсник

 Любой транзистор независимо от схемы включения обладает рядом параметров, которые возможно разбить на две группы:

-  предельные параметры – все максимальные значения;

- параметры транзистора в режиме малого сигнала.

Данные параметры объединяются в нес­колько систем параметров, которые можно определить, представив транзистор в виде активного четырехполюсника (рисунок 1.11). Четырехполюсником называется любое электрическое устройство, имеющее 2 входных и 2 выходных зажима. А активным четырехполюсником называется четырехполюсник, способный усиливать мощность.

\

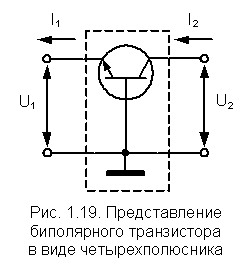Рисунок – 1.11 Представление биполярного транзистора в вмде четырехполюсника

Представим транзистор в виде активного четырехполюсника (рисунок 1.11). Присвоим входному току и напряжению индекс «1», а выходным индекс «2». Для транзисторов достаточно знать две любые переменные из четырех – U1, U2, I2,I1. Две остальные определяются из статических характеристик транзистора. Переменные, которые  известны или же которыми задаются, называются независимыми переменными. Две другие переменные, которые можно определить, называются зависимыми переменными. В зависимости от того, какие из переменных будут выбираться в виде независимых, можно получить системы параметров в режиме малого сигнала (таблица - 1).

Таблица 1. Системы параметров биполярного транзистора

Система параметров	Параметр
	Z	Y	H
Независимая переменная	I1, I2	U1, U2	I1, U2
Зависимая переменная	U1, U2	I1, I2	I2, U1

 

1.1.9 Система h- и y-параметров биполярного транзистора

В системе h-параметров в виде независимых переменных приняты входной ток и выходное напряжение. В этом случае зависимые переменные U1 = f (I1, U2); I2 = f (I1, U2). Полный дифференциал функций U1 и I2 равен

Введем следующие параметры

,  ,  ,  .

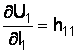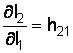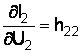Тогда система уравнений примет вид

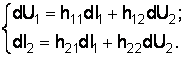
Перейдем от бесконечно малых приращений dU1, dI1, dU2, dI2 к конечным приращениям. Получим

В режиме малого сигнала приращение постоянных составляющих         можно заменить амплитудными значениями переменных составляющих этих же токов и напряжений. Получим

                                      (1.1)

В первом уравнении системы (1.1) приравниваем Um2 к 0. Получим

,

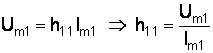следовательно   – это входное сопротивление транзистора при Um2 = 0, т. е. при коротком замыкании в выходной цепи по переменному току (конденсатором).

В первом уравнении системы (1.1) приравняем Im1 к 0. Получим

,

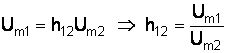тогда   представляет собой коэффициент обратной связи на холостом ходу во входной цепи по переменному току. Коэффициент обратной связи показывает степень влияния выходного напряжения на входное (катушкой индуктивности).

Во втором уравнении системы (1.1) приравняем Um2 к 0. Получим

  ,

т. е.   – коэффициент усиления по току транзистора или коэффициент передачи тока при коротком замыкании выходной цепи по переменному току.

Приравняем во втором уравнении системы (1.1) Im1 к 0. Получим

  ,

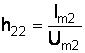тогда   – выходная проводимость на холостом ходу во входной цепи.