Лабораторная работа №2. Дешифрование, частотный анализ. Маскировка длины символа Дешифрование

Процесс нахождения открытого сообщения, соответствующего заданному закрытому, при неизвестном криптографическом преобразовании называется дешифрованием. Исследованием возможности дешифрования информации без знания ключей занимается криптоанализ.

Клод Шеннон ввел понятия диффузии и конфузии для описания стойкости алгоритма шифрования.

Диффузия – это рассеяние статистических особенностей и закономерностей незашифрованного текста в широком диапазоне статистических особенностей и закономерностей зашифрованного текста. Это достигается тем, что значение каждого элемента незашифрованного текста влияет на значения многих элементов зашифрованного текста или, что то же самое, любой элемент зашифрованного текста зависит от многих элементов незашифрованного текста.

Конфузия – это уничтожение статистической взаимосвязи между зашифрованным текстом и ключом.

Если Х – это исходное сообщение и K – криптографический ключ, то зашифрованный передаваемый текст можно записать в виде

Y = EK [X].

Получатель, используя тот же ключ, расшифровывает сообщение

X = DK [Y].

Противник, не имея доступа к K и Х, должен попытаться узнать Х, K или и то, и другое.

Частотный анализ

Шифры простой замены легко поддаются дешифровнию методом частотного анализа встречаемости букв и пар букв.

Все естественные языки и большинство искусственных имеют характерное частотное распределение букв и других знаков. Например, в английском языке буква E встречается наиболее часто, а буква Z – наиболее редкая (рис. 2).

Рис. 2. Частотность букв английского алфавита

Если подсчитать в зашифрованном сообщении частоты встречаемости символов и сопоставить их с характерными частотами для данного языка, то сообщение довольно легко может быть прочитано. Чем больше длина шифротекста, тем легче его дешифровать. Так же можно определить вероятности появления пар букв. Окажется, что для многих пар вероятность почти равна нулю. При дешифровании текста если встречается такая пара, то такой вариант отбрасывается.

Криптоаналитики часто используют индекс соответствия текстов, вычисляемый по формуле

г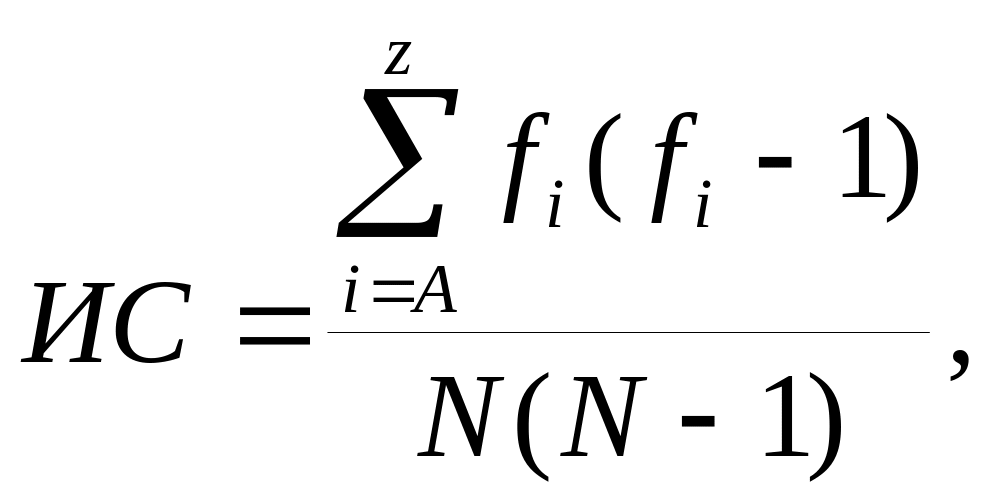 де f_i – общее число встречаемости буквы i в тексте;

N – общее число букв в тексте;

A – первая буква в алфавите;

z – последняя буква в алфавите.

По определению ИС представляет собой оценку суммы квадратов вероятностей каждой буквы. При многоалфавитной подстановке для английского языка, в зависимости от количества используемых при шифровании алфавитов (m), ИС ожидается:

m: 1 2 3 4 5 10

ИС: 0,066 0,052 0,047 0,045 0,044 0,041

При гаммировании криптостойкость определяется размером ключа. Покажем это на примере:

C₁ = P₁  K

С₂ = P₂  K

C₁  С₂ = P₁  P₂ ,

где K – символ гаммы;

P₁ и P₂ – символы разных открытых текстов, зашифрованных на одной гамме;

C₁ и С₂ – зашифрованные символы, соответствующие P₁ и P₂.

Далее, применяя к полученной сумме метод вероятностных слов или статистического анализа, есть вероятность найти оба открытых сообщения. На одном ключе может быть выработано конечное число символов гаммы, поскольку через определенное количество символов она начнет повторяться, то есть генератор гаммы всегда имеет некоторый период. Поэтому необходимо добиваться как можно большего периода или чаще менять секретный ключ.