Анализ и синтез систем автоматического управления при случайных воздействиях

Литература:

1. Теория автоматического управления: Учеб. для вузов по спец. “Автоматика и телемеханика”. В 2-х ч. Ч.II.Теория нелинейных и специальных систем автоматического управления/ А.А.Воронов, Д.П.Ким, В.М.Лохин и др.; Под ред. А.А.Воронова- 2-е изд., перераб. и доп.- М.: Высшая школа, 1986.-504с., ил.

2. Солодовников В.В., Плотников В.Н., Яковлев А.В. Теория автоматического

управления техническими системами: Учеб. пособие. – М.: Изд-во МГТУ,1993.-

492с., ил.

3. Теория автоматического управления: Учеб. для вузов/С.Е. Душин, Н.С. Зотов, Д.Х.

Имаев и др.; Под ред. В.Б. Яковлева.- М.: Высшая школа, 2003.-567с., ил.

Случайные события

Событие - результат (исход) опыта.

Случайное событие – это такое событие, которое может произойти или не произойти, причем это можно выяснить только в результате опыта.

Пример: число попаданий в мишень при N выстрелах.

Основная характеристика случайного события – его вероятность, то есть, частота появления события в большой серии опытов. Вероятность события – априорное знание.

Вероятность события А:

,

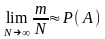где m - число исходов опытов, благоприятных событию А;

N - общее число всех равновозможных исходов опытов.

Исходы опытов (события) - равновозможны и несовместны.

Это приближенное равенство (теоретически) превращается в точное при стремлении числа опытов 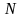к бесконечности. Например, если из партии в 1000 автомобилей 50 имеют дефекты (а остальные – исправны), то вероятность купить дефектный автомобиль, выбрав его наугад из этой партии, составляет 5%.

Случайные величины

Говоря о случайных событиях, мы рассматриваем только два варианта, «случилось» или «не случилось». Однако часто результаты эксперимента можно выразить в виде числа, количественно.

Величина - характеристика физических объектов или явлений материального мира, общая для множества объектов в качественном отношении, но индивидуальная в количественном отношении (обобщает такие понятия , как длина, площадь, сила и т. п.).

Случайная величина - величина, которая в каждом отдельном случае в зависимости от результатов опыта может принять то или иное числовое значение.

Предположим, что нас интересует сопротивление резисторов, купленных в магазине. Номинальное значение сопротивления, равно, например, 100 Ом. Однако, при изготовлении всегда есть допуски, то есть, разрешенные отклонения от номинала. Например, при допуске  3% сопротивление взятого наугад резистора может быть любым числом в интервале от 97 до 103 Ом.

Это – случайная величина. В общем случае интервал может быть и бесконечным, например, от 0 до бесконечности.

Х- случайная величина;

х- возможное значение случайной величины.

Примеры:

1. Размеры детали, обработанной на токарном станке;

2. Ошибка системы автоматического регулирования;

3. Число отказов прибора за определенное время работы;

4. Отклонение точки падения снаряда от цели является случайной двумерной

величиной:

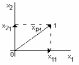
Задать случайную величину - указать все возможные ее значения и поставить им в соответствие вероятности, с которыми случайная величина принимает эти значения.

Различают непрерывные и дискретные случайные величины.

Вероятность каждого события лежит в интервале 0≤Р(А)≤1.

Вероятность невозможного события равна нулю.

Вероятность достоверного события равна единице.

Сумма всех вероятностей равна единице:

.

Введём обозначения: Х- случайная величина;

х- возможное значение случайной величины.

Значение случайной величины	x1	x2	………	xn
Вероятность события	Р(x1)	Р(x2)	………	Р(xn)