39

Лекция №6 Синтез систем автоматического управления

СИНТЕЗ САУ – выбор структуры и параметров САУ, начальных условий и входных воздействий в соответствии с требуемыми показателями качества и условиями функционирования.

Проектирование САУ предполагает выполнение следующих этапов:

1. Исследование объекта регулирования: составление математической модели, определение параметров, характеристик и условий работы объекта.

2. Формулирование требований к САР.

3. Выбор принципа управления; определение функциональной структуры (технический синтез).

4. Выбор элементов схемы регулирования с учетом статических, динамических, энергетических, эксплуатационных и др. требований и согласование их между собой по статическим и энергетическим характеристикам (процедура не формализована - инженерное творчество).

5. Определение алгоритмической структуры (теоретический синтез) производится с помощью математических методов и на основании требований, записанных в чёткой математической форме. Определение законов регулирования и расчет корректирующих устройств, обеспечивающих заданные требования.

6. Уточнение структурной схемы системы регулирования, выбора и расчета ее элементов и параметров.

7. Экспериментальное исследование системы (или отдельных ее частей) в лабораторных условиях и внесение соответствующих исправлений в ее схему и конструкцию.

8. Проектирование и производство системы регулирования.

9. Наладка системы в реальных условиях работы (опытная эксплуатация).

Проектирование САУ начинают с выбора объекта управления и основных функциональных элементов (усилителей, исполнительных устройств и др.), то есть разрабатывают силовую часть системы.

Заданные статические и динамические характеристики системы обеспечиваются соответствующим выбором структуры и параметров силовой части, специальных корректирующих устройств и всей САУ в целом.

Назначение корректирующих устройств: обеспечить требуемую точность работы системы и получить приемлемый характер переходного процесса.

Корректирующие звенья вводятся в систему различными способами: последовательно, местная ООС, прямое параллельное включение, внешние (вне контура регулирования) компенсирующие устройства, охват всей САУ стабилизирующей ООС, неединичная главная обратная связь.

Типы электрических корректирующих устройств постоянного тока: активные и пассивные четырехполюсники постоянного тока, дифференцирующие трансформаторы, тахогенераторы постоянного тока, тахометрические мосты и др.

По назначению корректирующие устройства классифицируются:

1. СТАБИЛИЗИРУЮЩИЕ – обеспечивать устойчивость САУ и улучшать их статические и динамические характеристики;

2. КОМПЕНСИРУЮЩИЕ – уменьшать статические и динамические ошибки при построении САУ по комбинированному принципу;

3. ФИЛЬТРУЮЩИЕ – повышение помехозащищенности систем, например фильтрация высших гармоник при демодуляции сигнала прямого канала;

4. СПЕЦИАЛИЗИРОВАННЫЕ – для придания системе особых свойств, позволяющих улучшить показатели качества системы.

САУ могут быть построены по следующим структурным схемам:

1. С последовательной корректирующей цепью.

Усилитель У должен иметь большое входное сопротивление, чтобы не шунтировать выход корректирующей цепи.

Применяется в случае медленно изменяющихся входных воздействиях, так как при больших рассогласованиях происходит насыщение в реальных нелинейных элементах, частота среза уходит влево и система медленно выходит из состояния насыщения.

Рис.1.

Последовательная коррекция часто используется в системах стабилизации либо для коррекции контура с корректирующей обратной связью.

- уменьшается.

2. Со встречно–параллельной корректирующей цепью.

Рис.2.

поступает на вход как разность и глубокого насыщения не наступает.

3. С последовательно–параллельной корректирующей цепью.

Рис.3.

4. С комбинированными корректирующими цепями.

Принцип построения многоконтурной САУ с каскадным включением регуляторов называют принципом подчинённого регулирования. Синтез САУ подчинённого регулирования с двумя и более контурами проводится путём последовательной оптимизации контуров, начиная с внутреннего.

Расчёт систем делится на 2 этапа: статический и динамический.

Статический расчёт заключается в выборе основных звеньев системы, входящих в её главную цепь, составление структурной схемы последней и определение параметров основных элементов системы (коэффициентов усиления, обеспечивающих требуемую точность, постоянных времени всех элементов, передаточных чисел, передаточных функций отдельных звеньев, мощности двигателя). Кроме того, сюда входит расчёт и проектирование магнитных и полупроводниковых усилителей и выбор транзисторных или тиристорных преобразователей, двигателей, чувствительных элементов и других вспомогательных устройств систем, а также расчёт точности в установившемся режиме работы и чувствительности системы.

Динамический расчёт включает большой комплекс вопросов, связанных с устойчивостью и качеством переходного процесса (быстродействием, характеристикой отработки и динамической точностью работы системы). В процессе расчёта выбираются корректирующие цепи, места их включения и определяются параметры последних. Проводится также расчёт кривой переходного процесса или моделирование системы с целью уточнения полученных качественных показателей и учёта некоторых нелинейностей.

Платформы, на которых строятся стабилизирующие алгоритмы:

1. Классическая (дифференциальные уравнения - временные и частотные методы);

2. Нечеткая логика;

3. Нейронные сети;

4. Генетические и муравьиные алгоритмы.

Методы синтеза регуляторов:

1. Классическая схема;

2. ПИД – регуляторы;

3. Метод размещения полюсов;

4. Метод ЛЧХ;

5. Комбинированное управление;

6. Множество стабилизирующих регуляторов.

Классический синтез регуляторов

Классическая структурная схема управления объектом приведена на рис. 1. Обычно регулятор включают перед объектом.

Рис. 1. Классическая структурная схема управления объектом

Задача системы управления состоит в том, чтобы подавить действие внешнего возмуще­ния и обеспечить качественные переходные процессы. Эти задачи часто противоречивы. Фактически нам нужно стабилизировать систему так, чтобы она имела требуемые передаточные функции по задающему воздействию и по каналу возмущения :

, .

Для этого мы можем использовать только один регулятор , поэтому такую систему называют системой с одной степенью свободы.

Эти две передаточные функции связаны равенством

.

Поэтому , изменяя одну из передаточных функций, автоматически меняем и вторую. Таким образом, их невозможно сформировать независимо и решение всегда будет некоторым компромиссом.

Посмотрим, можно ли в такой системе обеспечить нулевую ошибку, то есть, абсолютно точное отслеживание входного сигнала. Передаточная функция по ошибке равна

Для того, чтобы ошибка всегда была нулевой, требуется, чтобы эта передаточная функция была равна нулю. Поскольку ее числитель - не нуль, сразу получаем, что знаменатель должен обра­щаться в бесконечность. Мы можем влиять только на регулятор , поэтому получаем . Таким образом, для уменьшения ошибки нужно

увеличивать коэффициент усиления регулятора.

Однако нельзя увеличивать усиление до бесконечности. Во-первых, все реальные устрой­ства имеют предельно допустимые значения входных и выходных сигналов. Во-вторых, при большом усилении контура ухудшается качество переходных процессов, усиливается влияние возмущений и шумов, система может потерять устойчивость. Поэтому в схеме с одной степе­нью свободы обеспечить нулевую ошибку слежения невозможно.

Посмотрим на задачу с точки зрения частотных характеристик. С одной стороны, для ка­чественного отслеживания задающего сигнала желательно, чтобы частотная характеристи­ка была примерно равна 1 (в этом случае ). С другой стороны, с точки зрения робастной устойчивости нужно обеспечить на высоких частотах, где ошибка моде­лирования велика. Кроме того, передаточная функция по возмущению должна быть такой, что­бы эти возмущения подавлять, в идеале мы должны обеспечить .

Выбирая компромиссное решение, обычно поступают следующим образом:

● на низких частотах добиваются выполнения условия , что обеспечивает хорошее слежение за низкочастотными сигналами; при этом , то есть, низкочастотные возмущения подавляются;

● на высоких частотах стремятся сделать , чтобы обеспечить робастную устойчи­вость и подавление шума измерений; при этом то есть система фактиче­ски работает как разомкнутая, регулятор не реагирует на высокочастотные помехи.

Расчет линейных непрерывных САУ по заданной точности

в установившемся режиме работы

Одно из основных требований, которым должна удовлетворять САУ, заключается в обеспечении необходимой точности воспроизведения задающего (управляющего) сигнала в установившемся режиме работы.

Порядок астатизма и передаточный коэффициент системы находят исходя из требований к точности в установившемся режиме. Если передаточный коэффициент системы, определённый по требуемой величине статизма и добротности (в случае астатической САУ), оказывается настолько большим, что существенно затрудняет даже просто стабилизацию системы, целесообразно повысить порядок астатизма и этим свести до нуля заданную установившуюся ошибку вне зависимости от значения передаточного коэффициента системы. В результате становится возможным величину этого коэффициента выбирать, исходя только из соображений устойчивости и качества переходных процессов.

Пусть структурная схема САР приведена к виду

Тогда в квазиустановившемся режиме работы САР рассогласование представимо в виде сходящегося ряда

,

где выполняют роль весовых констант.

Очевидно, что такой процесс может иметь место только в том случае, если –медленно меняющаяся и достаточно плавная функция.

Если представить передаточную функцию разомкнутой системы в виде

,

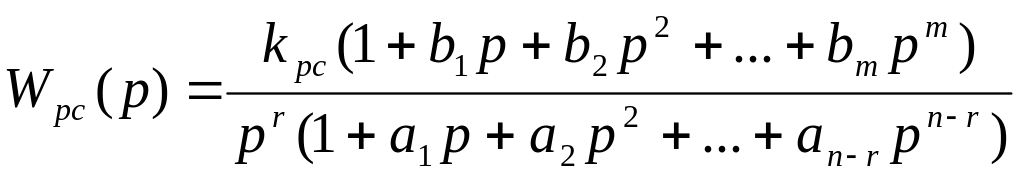то при r=0

при r=1

при r=2

при r=3

Низкочастотная часть логарифмических амплитудных частотных характеристик обусловливает точность работы системы при отработке медленно меняющихся сигналов управления в установившемся состоянии и определяется коэффициентами ошибок. Коэффициенты ошибок больше не оказывают существенного влияния на точность САУ, и их можно не учитывать при практических расчётах.

1. Расчет установившегося режима работы сар по заданным коэффициентам рассогласования (ошибки)

Точность работы системы в установившемся режиме определяется величиной передаточного коэффициента разомкнутой системы , который определяется в зависимости от формы задания требований к точности системы.

Расчет ведется следующим образом.

1. СТАТИЧЕСКИЕ САР. Здесь задается величина коэффициента позиционной ошибки 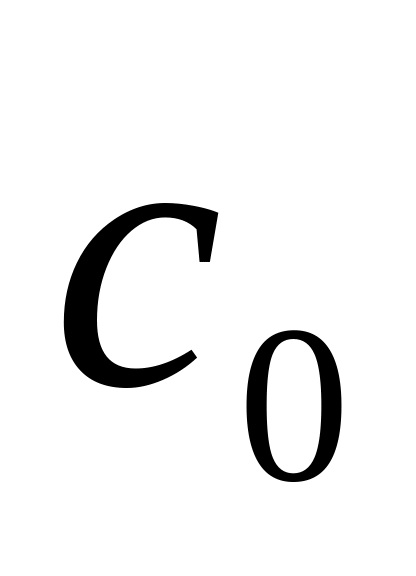, по которому определяется : .

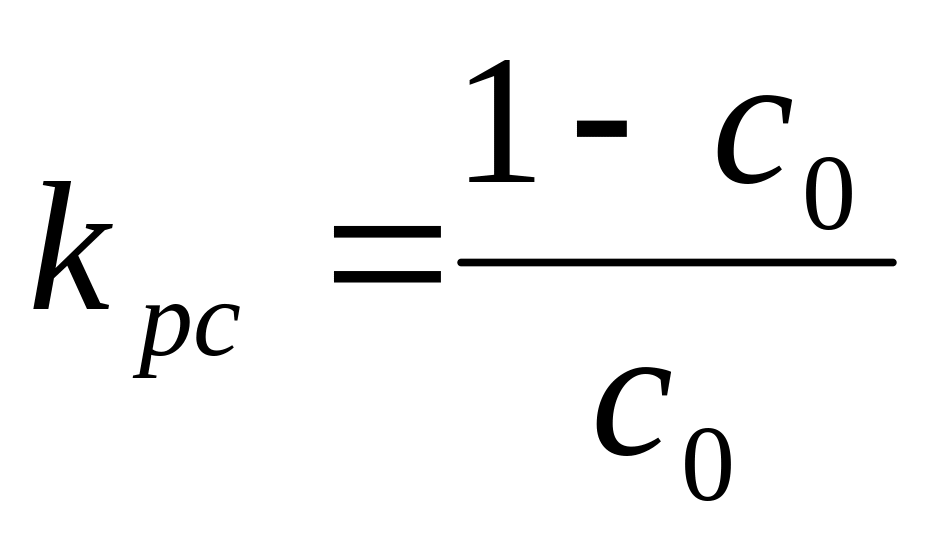L ,

дБ

20lgk_pc

ω, с^-1

2. АСТАТИЧЕСКИЕ СИСТЕМЫ 1-го порядка.

В этом случае задан коэффициент , по которому определяется

Если заданы коэффициенты и , то , который определяет положение низкочастотной асимптоты ЛАЧХ разомкнутой системы с наклоном -20 дБ/дек, а вторая асимптота имеет наклон -40 дБ/дек при сопрягающей частоте (рис.1).

Рис.1.

3. АСТАТИЧЕСКИЕ СИСТЕМЫ 2-го порядка.

По заданному коэффициенту определим k_pc:

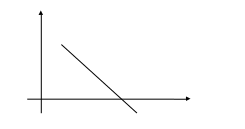
L,

дБ

-40

ω, с^-1

2. Расчет установившегося режима работы сар по заданной максимальной величине рассогласования (ошибки) системы

На основании допустимого значения установившейся ошибки и вида управляющего воздействия выбираются параметры низкочастотной части ЛАЧХ системы.

1. Пусть заданы допустимая максимальная ошибка 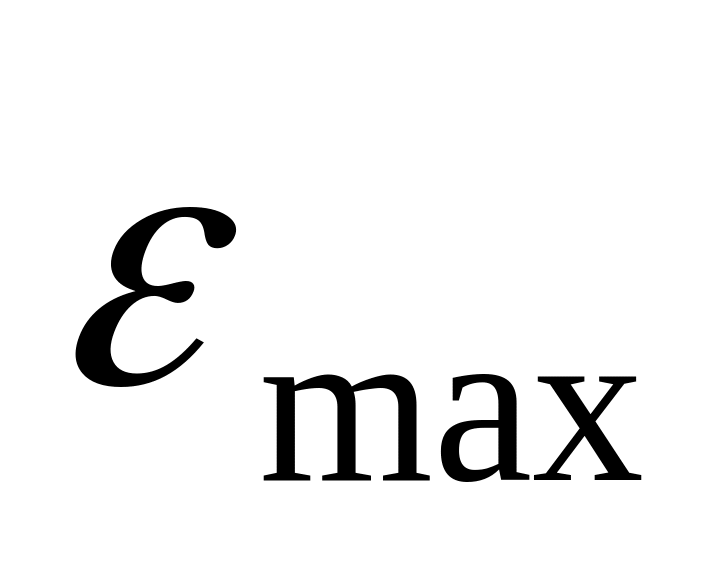при гармоническом воздействии с амплитудой 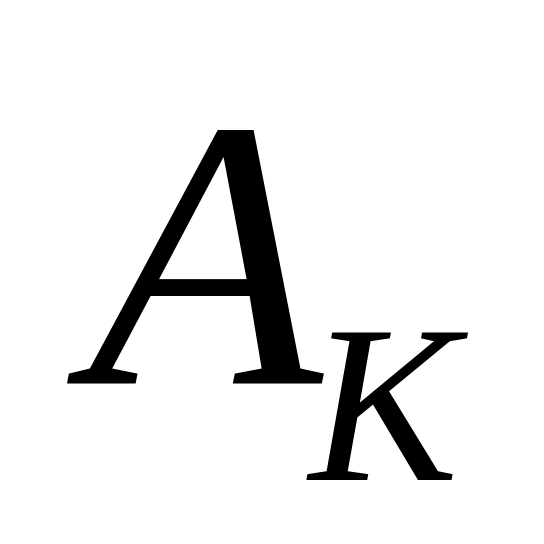и частотой 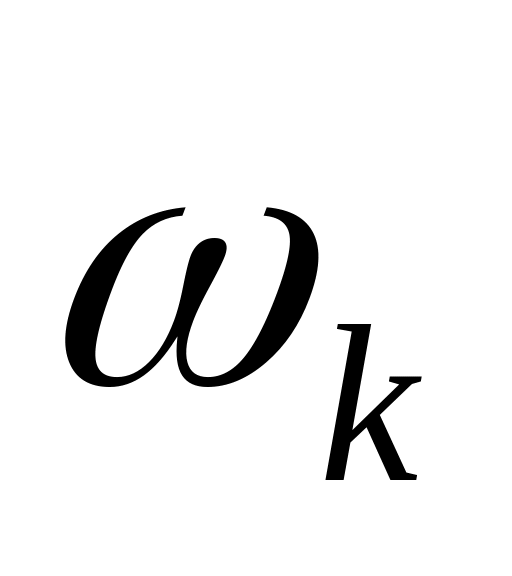и порядок 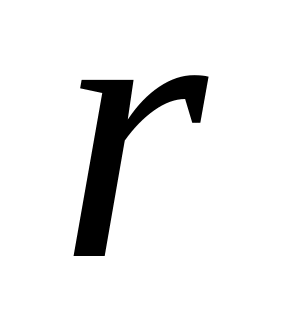астатизма системы.

Тогда низкочастотная асимптота ЛАЧХ системы должна проходить не ниже контрольной точки с координатами:

(1)

и иметь наклон -20r дБ/дек. Зависимость (1) справедлива при .

2. Пусть заданы допустимая максимальная ошибка при максимальной скорости 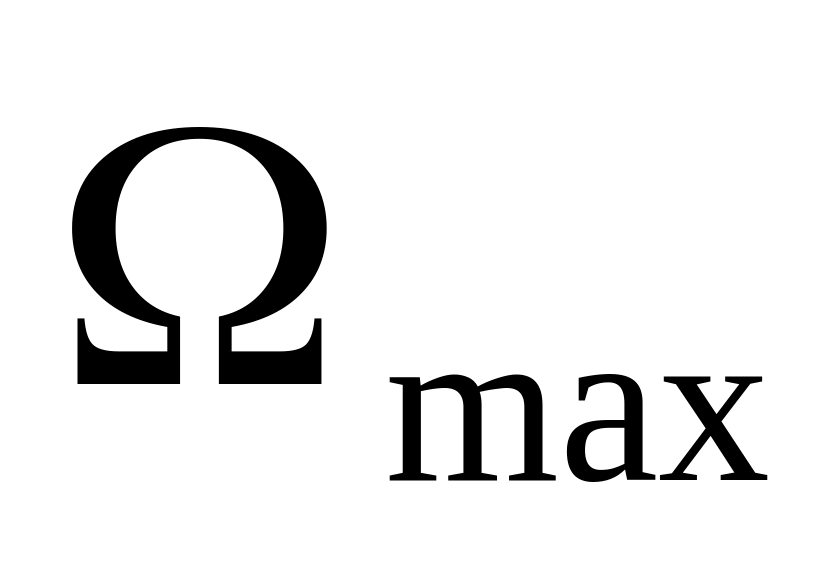и максимальное ускорение 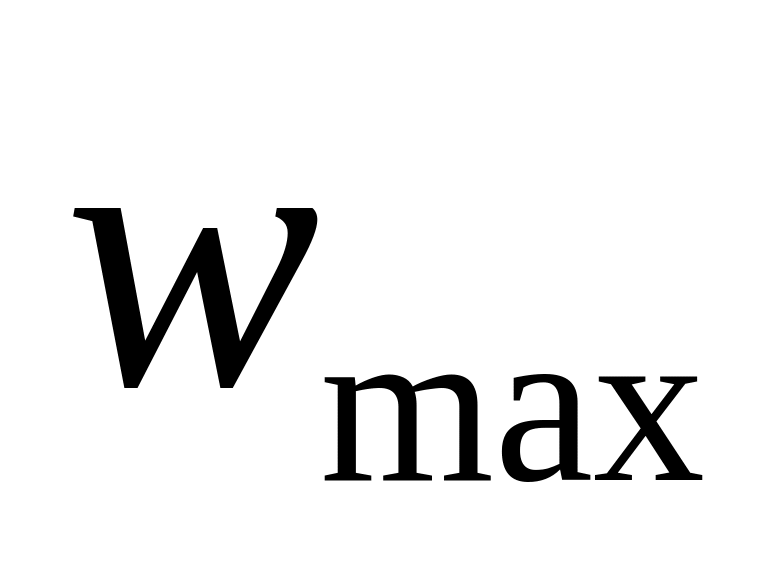входного воздействия и порядок астатизма r системы.

Часто удобно пользоваться методом эквивалентного синусоидального воздействия, предложенного Я.Е. Гукайло.

В этом случае определяется режим, при котором амплитуды скорости и ускорения равны максимальным заданным значениям. Пусть входное воздействие изменяется в соответствии с заданным законом

. (2)

Приравнивая амплитудные значения скорости и ускорения, полученные дифференцированием выражения (2), заданным значениям и , получим

откуда , . По этим величинам можно построить контрольную

точку В с координатами и

при единичной отрицательной обратной связи,

при неединичной обратной связи.

Если скорость сигнала на входе максимальна, а ускорение убывает, то контрольная точка будет двигаться по прямой с наклоном -20 дБ/дек в диапазоне частот . Если же ускорение равно максимальному значению, а скорость убывает, то контрольная точка движется по прямой с наклоном -40дБ/дек в диапазоне частот .

Область, расположенная ниже контрольной точки В и двух прямых с наклонами -20дБ/дек и -40дБ/дек, представляет собой запретную область для ЛАЧХ следящей системы. Так как точная ЛАЧХ проходит ниже точки пересечения двух асимптот на 3 дБ, то желаемая характеристика при должна быть поднята вверх на эту величину, т.е.

.

При этом требуемое значение добротности по скорости , а частота в точке пересечения второй асимптоты с осью частот (рис.2)

.

В том случае, когда управляющее воздействие характеризуется только максимальной скоростью, добротность системы по скорости при заданном значении ошибки:

.

Если задано только максимальное ускорение сигнала и величина ошибки, то добротность по ускорению:

.

Рис.2.

3. Пусть задана максимальная статическая ошибка по каналу управления 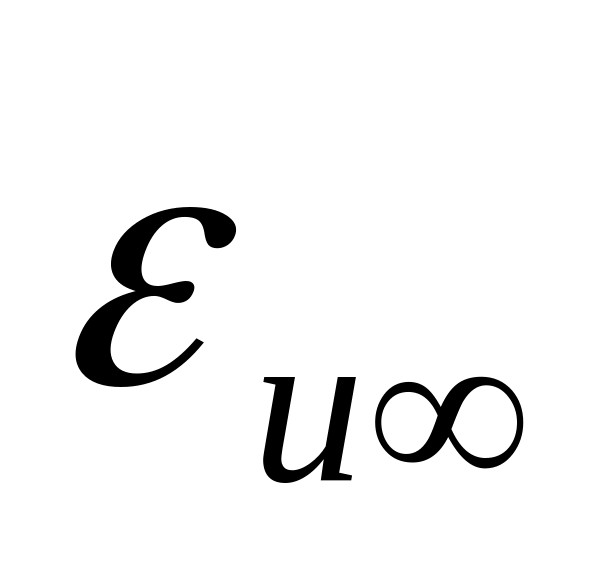(входное воздействие ступенчатое 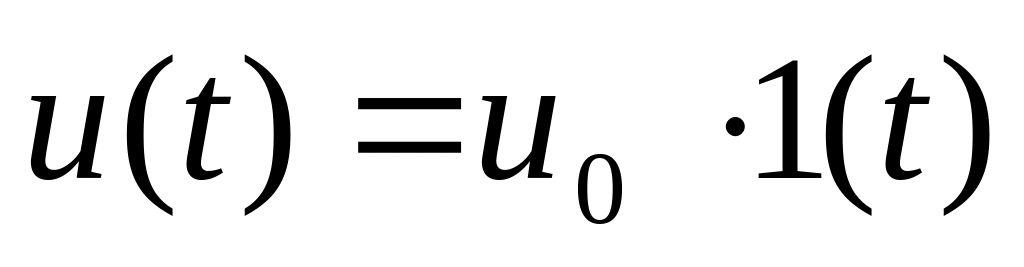, система статическая по каналу управления).

Рис.3.

Тогда величина определяется из выражения . Статическую точность автоматической системы можно определить из уравнения:

,

где – статическая точность замкнутой системы,

– отклонение регулируемой величины в разомкнутой системе,

– передаточный коэффициент разомкнутой системы, требуемый для обеспечения заданной точности.

4. Пусть задана максимальная допустимая статическая ошибка по каналу возмущения 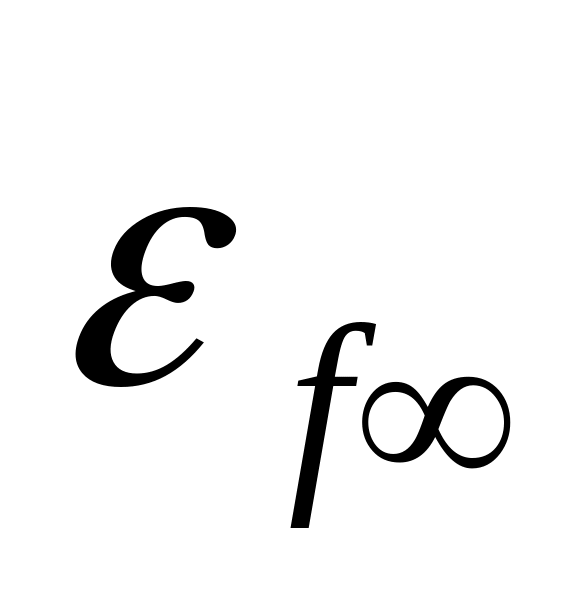(возмущающее воздействие ступенчатое 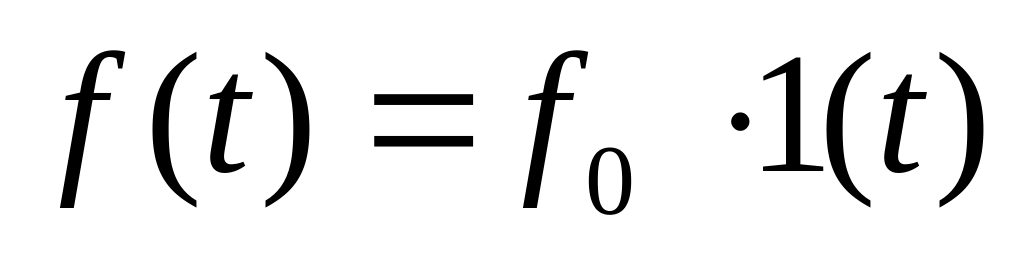, система статическая по каналу возмущения, рис.3).

Тогда величина определяется из выражения:

,

где – передаточный коэффициент разомкнутой системы по каналу возмущения,

где – ошибка системы без регулятора.

В статических системах управления установившаяся ошибка, вызванная постоянным возмущающим воздействием, уменьшается по сравнению с разомкнутой системой в 1+ . При этом в 1+ раз уменьшается также и передаточный коэффициент замкнутой системы.

5. Пусть задана допустимая скоростная ошибка от управляющего воздействия (входное воздействие изменяется с постоянной скоростью 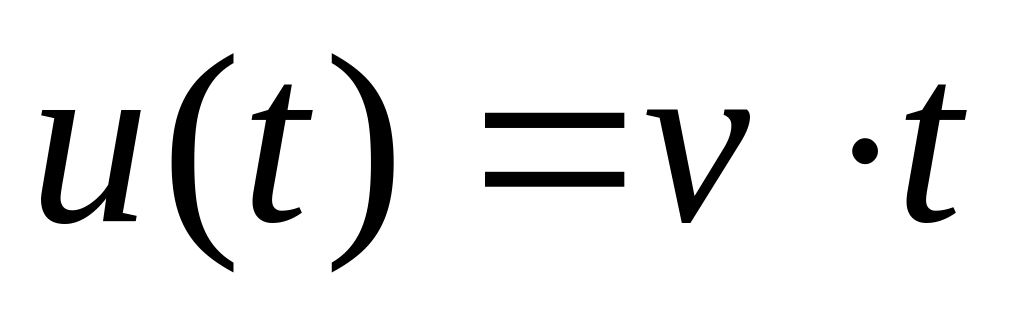, система астатическая первого порядка).

Следящие системы проектируют обычно астатическими первого порядка. Они работают при переменном управляющем воздействии. Для таких систем в установившемся режиме наиболее характерным является изменение входного воздействия по линейному закону.

Тогда добротность системы по скорости определяется из выражения:

.

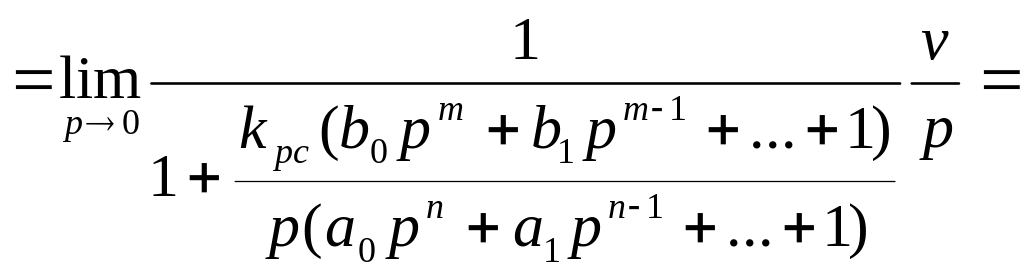
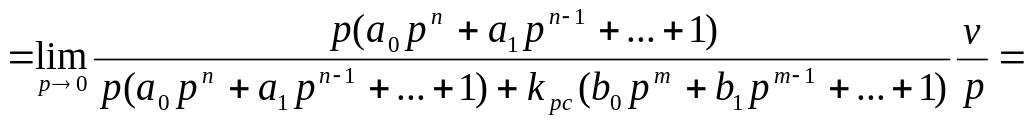
Поскольку установившаяся ошибка определяется низкочастотной частью ЛАЧХ, то по вычисленному значению передаточного коэффициента может быть построена низкочастотная асимптота желаемой ЛАЧХ.