20

Лекция №4

Устойчивость сау

Свойство системы приходить в исходное состояние после снятия возмущения называется устойчивостью.

О

САУ устойчива, если абсолютная величина отклонения регулируемой функции, получившаяся в результате возмущающего воздействия, по истечении достаточно большого промежутка времени после прекращения действия возмущения становится меньше наперёд заданного значения ε, т.е. .

пределение.

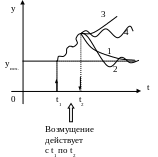
Кривые 1 и 2 характеризуют устойчивую систему, кривые 3 и 4 характеризуют системы неустойчивые.ε

Системы 5 и 6 на границе устойчивости 5 - нейтральная система, 6 - колебательная граница устойчивости.

Пусть дифференциальное уравнение САУ в операторной форме имеет вид

Тогда решение дифференциального уравнения (движение системы) состоит из двух частей Вынужденное движение того же вида что и входное воздействие.

При отсутствии кратных корней где С_i-постоянные интегрирования, определяемые из начальных условий,

₁, ₂…, _n – корни характеристического уравнения

Расположение корней характеристического

уравнения системы на комплексной плоскости

Корни характеристического уравнения не зависят ни от вида возмущения, ни от

начальных условий, а определяются только коэффициентами а₀, а₁, а₂,…,а_n, то есть параметрами и структурой системы.

1-корень действительный, больше нуля;

2-корень действительный, меньше нуля;

3-корень равен нулю;

4-два нулевых корня;

5-два комплексных сопряженных корня, действительная часть которых

положительна;

6-два комплексных сопряженных корня, действительная часть которых отрицательная;

7-два мнимых сопряженных корня.

Методы анализа устойчивости:

1. Прямые (основаны на решении дифференциальных уравнений);

2. Косвенные (критерии устойчивости).

Теоремы а.М. Ляпунова. Теорема 1.

Если определяющее (характеристическое) уравнение имеет корни только с отрицательными вещественными частями, то невозмущенное движение устойчиво и притом асимптотически, независимо от членов выше первого порядка малости.

Теорема 2.

Когда среди корней определяющего (характеристического) уравнения находятся такие, вещественные части которых положительные, невозмущенное движение неустойчиво.

Примечания:

1. Если среди корней характеристического уравнения имеется два и более нулевых корня, то система неустойчива.

2. Если один корень нулевой, а все остальные находятся в левой полуплоскости, то система нейтральна.

3. Если 2 корня мнимые сопряженные, а все остальные в левой полуплоскости, то система на колебательной границе устойчивости.