Статические характеристики звеньев и объектов сау

Статическая характеристика объекта

Статической характеристикой по каналу управления (возмущения) объекта называется функциональная зависимость выход-вход при отсутствии или постоянном значении возмущения (управления), все точки которой сняты в установившемся режиме (при t).

Пусть О₁ – рабочая точка объекта, тогда статический передаточный коэффициент объекта определяют по выражению:

.

Для характеристики динамических свойств в окрестности рабочей точки О₁ определяется приращение , соответствующее приращению ∆u входного воздействия. Чтобы упростить динамическую модель объекта производят линеаризацию характеристики. Достаточным условием возможности проведения линеаризации математической модели звена или системы является отсутствие разрывности и неоднозначности функций. Линеаризация нелинейной аналитической функции основана на том, что непрерывная и имеющая все производные в окрестности некоторой (рабочей) точки функция (например, статическая характеристика звена) может быть разложена в ряд Тейлора по степеням малых отклонений аргумента относительно рабочей точки:

.

Если при этом отклонения аргумента достаточно малы, то можно ограничиться первыми линейными членами разложения и рассматривать вместо нелинейной функции линейную, откуда

,

где - динамический передаточный коэффициент.

Линеаризацию нелинейных статических характеристик производят методами малых отклонений, касательной, секущей, кусочно – линейной аппроксимации.

У объектов регулирования определяют статические характеристики по каналам управления и возмущения:

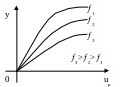
Возмущение обычно Внешние характеристики объекта

действует со знаком “-”

Пример

Линеаризация алгебраических уравнений

Резервуар с жидкостью

Бак с водой приведен на рис. 1. В нижней части бака просверлено отверстие, через которое вытекает вода. Площадь сечения бака обозначим через S, а площадь сечения отверстия – через .

Рис. 1. Резервуар с жидкостью

Построим модель, которая связывает уровень воды в баке (в метрах) и расход вытекающей воды (в м³/c). Эту связь можно найти с помощью закона Бернулли, который в данном случае принимает вид

,

где - плотность жидкости (в кг/м³), м/с² – ускорение свободного падения, - скорость вытекания жидкости (в м/с). Отсюда получаем . Учитывая, что расход воды вычисляется как , находим

, (1)

где - постоянная величина. Это статическая нелинейная модель. Статическая модель описывает установившееся состояние (статический режим), когда в баке поддерживается постоянный уровень воды и поток вытекающей воды тоже постоянный.

Линеаризовать модель – значит приближённо заменить нелинейное уравнение линейным:

,

где - некоторый коэффициент.

Предположим, что уровень воды изменяется в интервале от 0 до 1м. Тогда один из вариантов – вычислить коэффициент как угол наклона отрезка, соединяющего точки кривой на концах этого интервала. Для определённости принимаем , тогда получаем (рис.2). Эта модель очень грубая и даёт большую ошибку, особенно для уровней в диапазоне от 0,1 до 0,6. Чтобы уменьшить ошибку, можно попробовать несколько изменить (например, увеличив его до 1,2), однако точность приближения по-прежнему будет невысока, хотя и несколько лучше, чем в первом случае.

Рис. 2. Статические характеристики объекта

Теперь предположим, что обычно уровень мало изменяется вблизи среднего значения . В этом случае можно применить другой подход. В этой области кривая почти совпадает с касательной в точке (0,5; ), угол наклона которой равен производной

.

Касательная – это прямая с наклоном , проходящая через точку (0,5; ), её уравнение имеет вид . Свободный член определим из равенства

,

так что получаем модель

. (2)

Это линейное уравнение, однако модель (2) – нелинейная, поскольку для неё не выполняется, например, свойство умножения на константу. Это легко проверить, сравнив и :

.

Принцип суперпозиции также не выполняется.

Для того чтобы получить из (2) линейную модель, нужно записать уравнение в отклонениях от рабочей точки , в которой определили наклон касательной. Тогда

. (3)

Поскольку график зависимости (2) проходит через точку , можно применить равенство

.

Тогда из (3) находим

. (4)

Полученное таким образом уравнение – это линейная модель объекта, записанная в отклонениях входа и выхода от номинальной (рабочей) точки . Приближённая модель (4) точнее всего соответствует объекту вблизи этой точки, а при больших отклонениях от неё ошибка значительно возрастает.

Динамические характеристики:

1. Переходная характеристика;

2. Импульсная переходная характеристика;

3. Реакция объектов и систем на типовые и требуемые по технологии работы воздействия.

Типовые входные воздействия

1. Ступенчатое (скачкообразное) воздействие.

если U₀=1 [размерность входного воздействия], то u(t)=1(t) – единичное ступенчатое воздействие.

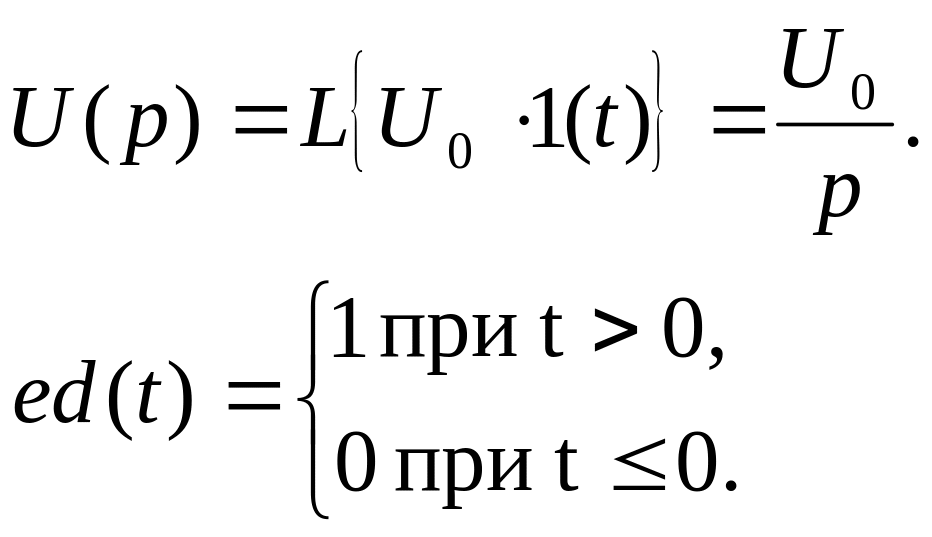
Функция Хевисайда (в Matlab – heaviside(t))

.

2. Линейно-возрастающее (с постоянной скоростью) воздействие.

где u(t) – линейная функция времени.

Для систем управления движением в качестве тестового сигнала обычно используют не функцию скачка, а линейно нарастающий сигнал, поскольку электромеханические системы имеют ограниченную скорость нарастания выходной функции.

3. Параболическое (с постоянным ускорением) воздействие.

где

4. Синусоидальное воздействие.

5. Воздействия в виде степенных функций времени.

изображение по Лапласу степенных функций времени имеет вид

При исследовании точности работы станков с программным управлением в установившихся режимах широко используются управляющие воздействия в виде степенных функций времени.

В нормальных режимах работы управляющее воздействие в виде линейной функции времени u(t)=At1(t) имеет место в следящих системах станков с программным управлением при обработке изделия с постоянной скоростью по одной или двум координатам. Управляющее воздействие в виде квадратичной степенной функции может быть, например, при обработке изделия с постоянным ускорением по одной из координат.

В ряде случаев более сложные воздействия на систему можно представить в виде суммы S степенных функций времени

6. Дельта-функция (единичная импульсная функция, функция Дирака (в Matlab – dirac(t))).

Р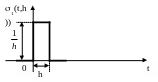 ассмотрим функцию

Если эту функцию трактовать как силу, действующую за промежуток времени от 0 до h, а в остальное время равную нулю, то, очевидно, импульс этой силы будет равен единице. Изображение этой функции будет т.е.

В механике и электротехнике удобно рассматривать силы, действующие очень короткий промежуток времени, как силы действующие мгновенно, но имеющие конечный импульс. Поэтому вводят функцию (t) как предел функции ₁(t,h) при

Следует иметь в виду, что (t) не есть функция в обычном понимании. Многие авторы-физики функцию (t) называют функцией Дирака.

Эту функцию называют также единичной импульсной функцией или дельта-функцией. Естественно положить

L – изображение функции (t) определим как предел изображения функции ₁(t,h) при (здесь воспользовались правилом Лопиталя для нахождения предела).