
- •Механизм, машина, звено, стойка, входные и выходные звенья. Кинематические пары и их классификация. Кинематические цепи: плоские и пространственные, замкнутые и незамкнутые.
- •Число степеней свободы пространственных и плоских механизмов.
- •Принцип Ассура образования плоских рычажных механизмов. Структурные группы и их классификация.
- •4. Кинематический анализ плоских рычажных механизмов графическим методом.
- •5. Функции положения, аналоги скоростей и ускорения звеньев и точек.
- •6. Кинематический анализ плоских рычажных механизмов аналитическим методом.
- •7 Виды зубчатых передач. Передаточное отношение, передаточное число.
- •8. Определение передаточных отношений ступенчатых зубчатых передач с подвижными осями вращения.
- •9. Виды зубчатых механизмов с подвижными осями вращения. Формула Виллиса для дифференциальных и планетарных механизмов.
- •10. Классификация сил действующих в машинах.
- •11. Динамическая модель машины с одной степенью свободы. Приведение сил и масс.
- •12. Уравнение движения звена приведения в энергетической и дифференциальной формах.
- •13. Режимы движения машин. Коэффициент неравномерности движения.
- •14. Определение закона движения звена приведение из уравнения движения в энергетической форме.
- •18. Метод кинетостатики. Определение сил инерции звеньев.
- •19. Условие статической определимости плоских кинематических цепей.
- •20. Кинетостатический силовой анализ плоских рычажных механизмов аналитическим методом.
- •21. Основные закономерности сухого трения скольжения. Коэффициент, угол и конус трения. Трение в поступательной кинематической паре. Приведенный коэффициент трения в кленовых направляющих.
- •22. Трение скольжения во вращательной кинематической паре. Круг трения. Приведенный коэффициент трения.
- •24. Механический кпд и коэффициент потерь. Кпд при последовательном и параллельном соединении механизмов.
- •Кпд передачи винт - гайка. Самоторможение. Кпд червячной передачи.
- •Динамическое и статическое уравновешивание вращающихся звеньев. Виды неуравновешенности, их оценка и способы устранения. Балансировка.
- •27Уравновешивание нескольких масс, вращающихся на одном валу
- •28 Статическое уравновешивание масс плоских рычажных механизмов (методом статического размещения масс).
- •29.Основная теорема плоского зацепления. Следствия.
- •30.Эвольвента окружности, ее уравнение и свойства
- •31 Основные геометрические параметры зубчатых колес.
- •32 Свойства и характеристики эвольвентного зацепления цилиндрических зубчатых колес Условия отсутствия интерференции зубьев
- •34 Основная теорема зацепления зубчатого механизма.
- •35. Эвольвета окружности. Её уравнения и свойства.
- •36. Основные геометрические параметры зубчатого колеса
- •38. Качественные показатели зубчатого зацепления.
- •39. Методы нарезания зубчатых колёс.
7 Виды зубчатых передач. Передаточное отношение, передаточное число.
Простые зубчатые передачи классифицируются:
по виду передаточной функции (отношения)
с постоянным передаточным отношением;
с переменным передаточным отношением;
по расположению осей в пространстве
с параллельными осями;
с пересекающимися осями;
с перекрещивающимися осями;
по форме профиля зуба
эвольвентным профилем;
с круговым профилем (передачи Новикова);
по форме линии зуба
с прямым зубом;
косозубые;
шевронные;
по форме начальных поверхностей
цилиндрические;
коническое;
по форме и виду зубчатых колес
червячные;
винтовые.
Передаточное отношение зубчатой передачи – отношение угловой скорости входного вала к угловой скорости выходного. Передаточное число зубчатой передачи – отношение числа зубьев ко-леса к числу зубьев шестерни.
![]()
8. Определение передаточных отношений ступенчатых зубчатых передач с подвижными осями вращения.
Зубчатая передача – трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную или поступательную пару.
Передаточное отношение U12 (иногда используется обозначение i12) определяется при ведущем колесе 1, передаточное отношение U21 определяется если ведущим является колесо 2:


Планетарными называются передачи, в которых оси одного или нескольких колес закреплены в подвижном звене – водиле. Любая планетарная передача состоит из трех групп элементов. Первая группа – центральные колеса (колеса, расположенные на неподвижных осях), вторая группа – сателлиты (колеса, расположенные на подвижном звене – водиле) и третья группа – водила. схема передачи, состоящей из центрального колеса 1, сателлита 2 и водила H.
В общем случае центральное колесо и водило могут получать вращение от двух источников независимо друг от друга. Такая передача имеет две степени свободы и называется дифференциальной.
Если закрепить центральное колесо, то получается передача с одной степенью свободы – движение можно передавать либо от водила к сателлиту, либо от сателлита к водилу – такая передача называется простой планетарной (рис. 238).
Сателлиты планетарных передач совершают сложное вращательное движение. Движение сателлитов относительно Земли (относительно неподвижной системы координат) складывается из вращения их вместе с водилом – переносного движения и вращения их вокруг осей, закрепленных в водиле, – относительного движения

9. Виды зубчатых механизмов с подвижными осями вращения. Формула Виллиса для дифференциальных и планетарных механизмов.
Две или более зубчатые передачи образуют зубчатый механизм.
Зубчатые колеса, зубчатые передачи и зубчатые механизмы чрезвычайно разнообразны. Поэтому целесообразно ознакомиться с их простейшей классификацией.
Зубчатые колеса бывают:
а) цилиндрические и конические,
б) прямозубые, винтовые, шевронные,
в) эвольвентные, циклоидальные, цевочные, трохоидальные, круговинтовые
г) с внешним и с внутренним зацеплением.
Винтовые колеса могут быть с левым и с правым наклоном зуба. Винтовые колеса с винтовой линией постоянного шага называют косозубыми.
Зубчатые передачи бывают:
а) с постоянным и переменным передаточным отношением некруглые колеса),
б) плоские и пространственные,
в) с параллельными, пересекающимися и скрещивающимися осями колес.
По этому признаку различают цилиндрические, конические, гиперболоидные передачи.
Для кинематического анализа механизмов с подвижными осями применяется метод обращенного движения. Сущность метода состоит в том, что всем звеньем условно сообщается дополнительное вращение с общей угловой скоростью –ωН, равной угловой скорости водила ωН, но противоположно ей направленной. Тогда угловые скорости звеньев обращенного механизма будут равны
 =ω1-
ωН;
=ω1-
ωН;
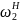 =ω2-
ωН;
=ω2-
ωН;
 =ω3-
ωН;
=ω3-
ωН;
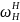 =ωН-
ωН=0.
=ωН-
ωН=0.
Поскольку
угловая скорость водила в обращенном
движении равно 0, то обращенный механизм
является механизмом с неподвижными
осями колес, и для него можно записать
придатчное отношение
 ,
выражая его через числа зубьев по
формулам для ступенчатого и паразитного
рядов.
,
выражая его через числа зубьев по
формулам для ступенчатого и паразитного
рядов.
Формула Виллиса для дифференциального механизма:
 =
=
=ω1- ωН;
Планетарные механизмы являются частным случаем дифференциальных механизмов, когда одно из центральных колес заторможено, и степень подвижности механизма W=1. Для них число степеней подвижности равно w=3n-2p5-p4=3*3-2*3-2=1.
