Механизм, машина, звено, стойка, входные и выходные звенья. Кинематические пары и их классификация. Кинематические цепи: плоские и пространственные, замкнутые и незамкнутые.
Механизм, машина, звено, стойка, входные и выходные звенья.
Механизм – Система тел предназначенная для передачи и преобразования механических движений
Машина –устройство выполняющая механические движения для преобразования энергии материалов и информации
- энергетические
- технологические
- транспортные
- информационные
Звено – одно или несколько жестко соединённых твердых тел входящих в состав механизмов
Стойка – звено неподвижное или принимаемое за неподвижное
Входное звено(вход) – звено которому сообщается движение
Выходное звено(выход) – звено совершающее движение для выполнения которого требуется механизм
Кинематические пары и их классификация.
Кинематическая пара – это подвижная соединение 2х соприкасающихся звеньев.
По числу степеней свободы в относительном числе звеньев, все кинематические пары делятся на:
1, 2, 3, 4, 5, 6-подвижные пары =>
По классам
1 подвижные - 5класс
2 подвижные – 4класс
……………………….
5 подвижные – 1 класс
Различают кинематические пары:
Вращательные
Поступательные
Цилиндрические
Сферическая или шаровая
По характеру соприкосновения:
Нисшие – соприкосновение звньев по поверхности
Высшие – по линиям или в точках
Кинематические цепи: плоские и пространственные, замкнутые и незамкнутые.
Кинематические цепи – Система звеньев образующих между собой кинематические пары
Бывают:
Плоские - все подвижные точки которого движутся в параллельных плоскостях
Пространственные - подвижные точки которого описывают неплоские траектории или траектории, лежащие в пересекающихся плоскостях.
Замкнутые и незамкнутые.
Число степеней свободы пространственных и плоских механизмов.
обобщенными координатами механизмов - называют число независимых между собой параметров определяющих положения всех звеньев относительно стоийки,
где, n-число подвижных звеньев
.
– Число кинематических пар
Для пространственных механизмов
W=
-
Для плоских механизмов
W=
.
– число нисших кинематических пар
.
– число высших кинемат. Пар
За обобщенную координату применяется угол φ1 с поворотом (0≤ φ1≤360°(
Начальное звено – звено к которому приписана обобщенная координата.
Принцип Ассура образования плоских рычажных механизмов. Структурные группы и их классификация.
Структурная группа (кинематическая цепь), число степеней свободы которой относительно элементов ее внешних кинематических пар равно нулю (причем из нее нельзя выделить более простые кинематические цепи, удовлетворяющие этому условию) называется группой Ассура.
В
группах Ассура звенья образуют только
кинематические пары 5-го класса.
тогда
Это
условие в целых числах удовлетворяется
только при четных числах звеньев п и
числах низших кинематических пар p 5 ,
кратных трем, и может быть представлено
соотношениями
-
Число подвижных
звеньев
п
2
4
6
8
Число кинематических пар 5-го класса
p5
3
6
9
12
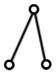
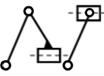
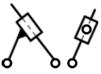
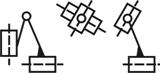
Наиболее простые структурные группы с п = 2 и p 5 = 3 Их называют двухповодковыми группами Ассура или структурными группами II-го класса второго порядка Различают пять видов групп Ассура второго класса, отличающихся друг от друга только соотношением между числом вращательных и поступательных кинематических пар и порядком их расположения.
Класс |
Порядок второй |
||||
Вид |
|||||
первый |
второй |
третий |
четвертый |
пятый |
|
II n = 2 р5 = 3 |
|
|
|
|
|
