3.2. Пространственная когерентность. Ширина когерентности

Понятие «точечный источник» — это такая же идеализация, как и монохроматическая волна. Все реальные источники являются протяженными, а это приводит к уменьшению контраста интерференционной картины. Опыт показывает, что при увеличении размеров источника видимость интерференционной картины постепенно уменьшается и при достаточно больших размерах интерференционные полосы полностью исчезают. Качественно характер изменения видимости полос при увеличении размеров источника можно понять, если предположить, что протяженный источник состоит из независимых излучателей (Рис. 3.3).

Рис.3.3. Интерференция от протяженного источника.

Действительно, весь источник света можно «разбить» на малые площадки с линейным размером много меньше длины волны, состоящие из атомов, излучающих независимо от атомов другой площадки , поэтому волны, излучаемые этими площадками, являются некогерентными и интерференции между ними не будет.

Этот же случай можно рассмотреть на примере с двойной щелью. До сих пор щель в опыте Юнга, по умолчанию, предполагалась весьма узкой (часто говорят бесконечно узкой). Расширение же щели, как и уменьшение степени монохроматичности света, приводит к ухудшению (размытию) интерференционных полос и даже к полному их исчезновению. Чтобы выяснить роль ширины щели , рассмотрим теперь на примере опыта Юнга другой крайний случай: излучение монохроматическое, щель не узкая.

Интерференционную картину на экране (рис. 3.4 и рис. 3.5) можно представить как наложение интерференционных картин от бесконечно узких щелей, на которые мысленно разобьём щель .

Рис. 3.4 Рис. 3.5

Пусть положение максимумов на экране от узкой щели, взятой около верхнего края щели – точки 1 — таково, как отмечено сплошными отрезками на рис. 3.4. А максимумы от узкой щели, взятой около нижнего края щели — точки 2, будут смещены вверх, они отмечены пунктирными отрезками на этом же рисунке. Интервалы между этими максимумами заполнены максимумами от промежуточных узких щелей, расположенных между краями 1 и 2.

При расширении щели расстояния между максимумами от её крайних элементов будут увеличиваться, т. е. интервалы между соседними максимумами от одного края щели будут постепенно заполняться максимумами от остальных элементов щели.

Для простоты будем считать, что в схеме (рис. 3.5) расстояния . Тогда при ширине щели , равной ширине интерференционной полосы ( ), интервал между соседними максимумами от края 1 будет целиком заполнен максимумами от остальных элементов щели, и интерференционные полосы исчезнут.

Итак, при расширении щели интерференционная картина постепенно размывается и при некоторой ширине щели практически исчезает.

Это наблюдаемое явление можно объяснить и иначе, а именно: интерференционная картина исчезает вследствие того, что вторичные источники – щели и становятся некогерентными. Сказанное позволяет говорить о ширине когерентности падающей на щели S₁ и S₂ световой волны – ширине , на которой отдельные участки волны в достаточной степени когерентны и дают интерференционную картину. Во избежание недоразумений уточним: под шириной когерентности понимается характерное для данной установки расстояние между точками поверхности, перпендикулярной направлению распространения волны.

Найдём формулу для вычисления . В рассматриваемой схеме опыта Юнга очевидно, что минимальная ширина когерентности падающей волны не может быть меньше расстояния между щелями , т.е. условие, при котором щели и становятся когерентным, есть следующие:

, (3.4)

где - расстояние между щелями. Кроме того, мы выяснили, что интерференционная картина исчезнет когда, когда ширина первичной щели равна ширине интерференционного максимума (т.е. условие, при котором щели становятся не когерентными):

. (3.5)

Ширина интерференционного максимума, согласно формуле (2.7), равна . Из этих трёх равенств получим:

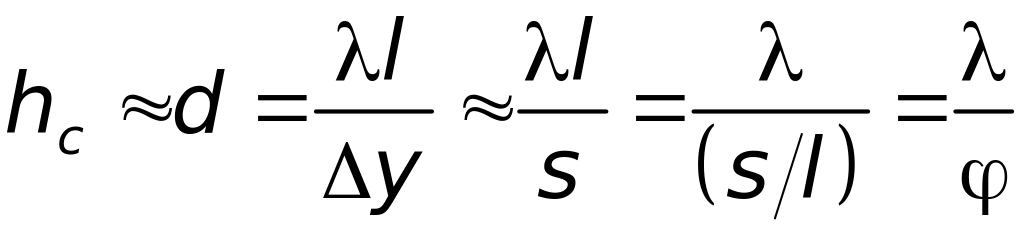, (3.6)

где - угловая ширина щели относительно диафрагмы с двумя щелями. Итак, ширина когерентности

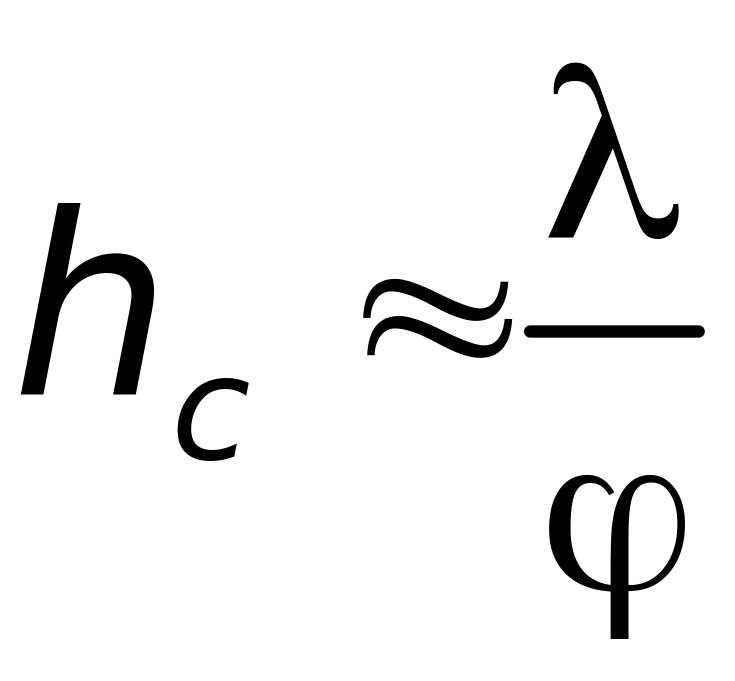. (3.7)

Таким образом, ширина когерентности пропорциональна длине волны и обратно пропорциональна угловой ширине источника относительно интересующего нас места (в опыте Юнга – относительно места расположения двух щелей). Сказанное поясняет рис. 3.6.

Рис. 3.6

Если в качестве источника использовать непосредственно Солнце (его угловой размер рад и мкм.), то ширина когерентности, согласно (3.6), мм. Для получения интерференционной картины от двух щелей с помощью такого излучения расстояние между двумя щелями должно быть меньше 0,05 мм, что сделать практически невозможно.

Из сказанного в предыдущем разделе следует, что временная когерентность связана с разбросом значений , и, следовательно, с разбросом значений модуля волнового вектора , где единичный вектор, совпадающий с направлением распространения световой волны. Пространственная когерентность связана с разбросом направлений вектора , который характеризуется величиной .

Формула (3.4) по существу лежит в основе метода, предложенного Физо и осуществленного Майкельсоном, по определению угловых размеров звёзд путем измерения ширины когерентности. Попытки провести эти измерения, помещая экран с двумя щелями перед объективом телескопа, оказались безуспешными: полосы интерференции оставались четкими даже при наибольшем расстоянии между этими щелями. Майкельсон преодолел эту трудность с помощью звездного интерферометра (рис. 3.7). Расположенные против щелей зеркала – — неподвижны, а зеркала — можно одновременно раздвигать, меняя расстояние между ними. Видимость полос зависит от степени когерентности световых колебаний на зеркалах — , в то время как ширина полос определяется расстоянием между щелями. Постепенно раздвигая зеркала — , обнаруживают, что при определенном расстоянии между ними интерференционная картина исчезает. Это значит, что расстояние между этими зеркалами оказалось таким, что . Остается по формуле (3.4.) вычислить . При максимальном расстоянии м. можно было измерить угловой диаметр объекта угл. сек.

Рис. 3.7

Первой звездой, угловой диаметр которой удалось определить, была Бетельгейза (0,047 угл. сек.). Измерив, кроме того, расстояние до неё (по параллаксу), определили диаметр этой звезды-гиганта (он оказался больше диаметра земной орбиты!).

Объём когерентности. Всё пространство, занимаемое волной, можно разбить на части, в каждой из которых волна приблизительно сохраняет когерентность. Объём такой части пространства, называемой объёмом когерентности, по порядку величины равен произведению длины когерентности на площадь круга, радиуса равного ширине когерентности

. (3.5)

Общие выводы. Для получения устойчивой интерференционной картины с использованием обычных (не лазерных) источников света необходимо исходную световую волну расщепить подходящим способом на две части, которые затем в области перекрытия и дадут систему полос, но лишь в том случае, если у исходной световой волны:

1) длина когерентности превышает оптическую разность хода складываемых колебаний и

2) ширина когерентности превышает расстояние между щелями.

Насколько больше должны быть эти величины общепринятого соглашения нет. Будем считать, например, вдвое. Тогда можно записать:

(3.6)

. (3.7)

Выполнение этих условий гарантирует получение интерференционной картины с достаточно хорошей видимостью полос.