2. Опыт юнга. Расчёт интерфернционной картины от двух щелей

В оптике явление интерференции впервые наблюдалось Юнгом в 1801 г. (рис. 2.3). Здесь свет от источника проходит сначала через маленькое отверстие в экране S, а затем падает на другой экран с двумя маленькими отверстиями S₁ и S₂, разнесенными на некоторое расстояние . Прошедший через отверстия свет падает на экран Э, где и наблюдается интерференционная картина. Опыт Юнга был первым убедительным доказательством того, что наложение света может образовать темноту, а наблюдение интерференции в опыте Юнга явилось экспериментальным доказательством волновой природы света.

y

_l

Рис. 2.3. Опыт Юнга.

Рис. 2.4.

Когерентные световые волны можно получить, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. Если потом заставить эти две волны пройти разные оптические пути, а потом наложить друг на друга, наблюдается интерференция. Разность оптических длин путей, проходимая интерферирующими волнами, не должна быть очень большой, так как складывающиеся колебания должны принадлежать одному и тому же результирующему цугу волн.

Р

Рис. 2

ассмотрим две сферические или цилиндрические световые волны, исходящие из источников и , имеющих вид светящихся точек или щелей, расположенных на расстоянии (Рис. 2.4). Экран Э параллелен щелям и находится от них на расстоянии , при этом . Область, в которой волны перекрываются, называется полем интерференции.

Найдём положение максимумов и минимумов на интерференционной картине от двух щелей. Интенсивность в произвольной точке А, находящейся на расстоянии от центра интерференционной картины в точке О , определяется разностью хода двух волн:

. (2.1)

Из геометрических построений на рис. 2.4 видно, что:

, (2.2)

.

Вычитая из первого уравнения второе и пренебрегая членом , получим:

.

Отсюда:

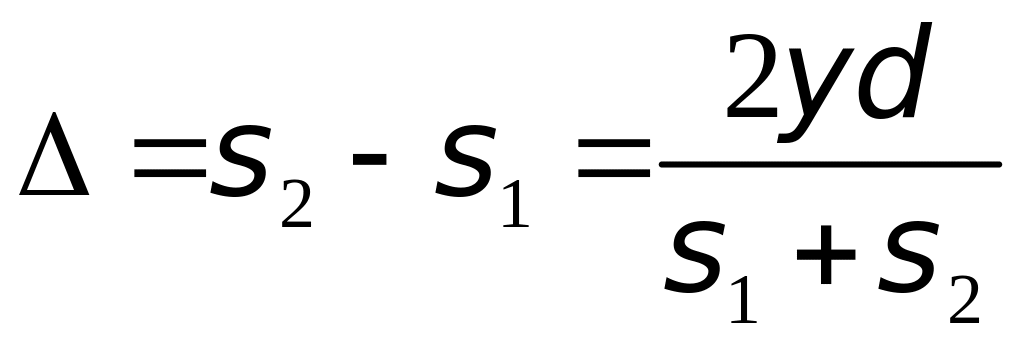. (2.3)

Из условия следует , поэтому оптическая разность хода в точке А равна:

. (2.4)

Подставив выражение для разности хода (2.4) в условие наблюдения максимума (1.16) и минимума (1.18), получим выражение для расстояний от центра и для максимумов и минимумов интенсивности света:

положение максимумов при отсюда:

( ), (2.5)

положение минимумов при

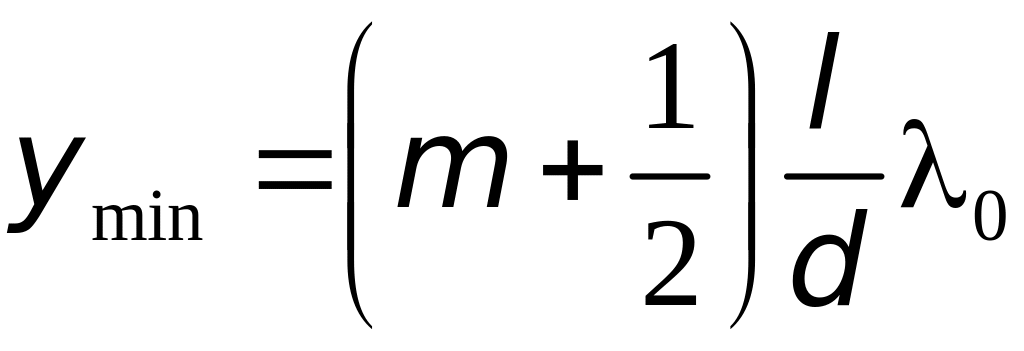( ). (2.6)

2.1. Ширина интерференционной полосы

Из (2.5) следует, что в точке расположен максимум, соответствующий нулевой разности хода. Для него порядок интерференции . Это центр интерференционной картины. При переходе к соседнему максимуму меняется на единицу и — на величину . Расстояние между двумя соседними максимумами (или минимумами) называется шириной интерференционной полосы. Из формулы (2.5) или (2.6) легко получить:

.

Отсюда следует, что ширина интерференционной полосы определяется выражением:

(2.7)

Согласно формуле (2.7), расстояние между полосами растёт с уменьшением расстояния между щелями и с увеличением расстояния до экрана . При , сравнимом с , расстояние между полосами было бы одного порядка с , и составляло бы несколько десятка мкм. В этом случае отдельные полосы были бы совершенно неразличимы, поскольку разрешающая способность глаза ≈ 0,1мм, а длина волны света ≈ 0,5мкм, т.е. на три порядка меньше. Для того чтобы интерференционная картина стала отчётливой, необходимо соблюдение упоминавшегося выше условия .

Период, положение и контрастность интерференционных полос зависят от основных параметров источников излучения: их длины волны (или частоты), начальной фазы, соотношения амплитуд, а также от взаимного расположения источников. Проследим это влияние на модельных экспериментах.

Влияние расстояния между источниками излучения на интерференционную картину продемонстрировано на рис. 2.5.

Рис. 2.5. Влияние расстояния между источниками на ширину интерференционных полос: в случае (а) расстояние в два раза больше, чем в случае (б).

На этом рисунке полосы от двух точечных источников в области чередования тёмных и светлых участков (гребней и впадин волн) соответствуют максимумам интерференционной картины, а расходящиеся веером серые полосы — интерференционным минимумам. Как и следует из формулы для ширины интерференционной полосы (2.7), при сближении источников (рис. 2.5б) период интерференционной картины возрастает.

Изменение длины волны источников моделируется на рис. 2.6. При неизменном расстоянии между ними с увеличением длины волны (рис. 2.6б) ширина интерференционной полосы возрастает, чтобы набрать прежнюю разность хода, теперь нужно большее расстояние.

Рис. 2.6. Влияние длины волны на ширину интерференционных полос:

в случае (а) длина волны в два раза меньше, чем в случае (б).

Введём в рассмотрение угол - угол, под которым видны щели S₁ и S₂ из центра интерференционной картины. Из рис. 2.7 видно, что , поэтому формулу для ширины интерференционной полосы (2.7) можно переписать в виде:

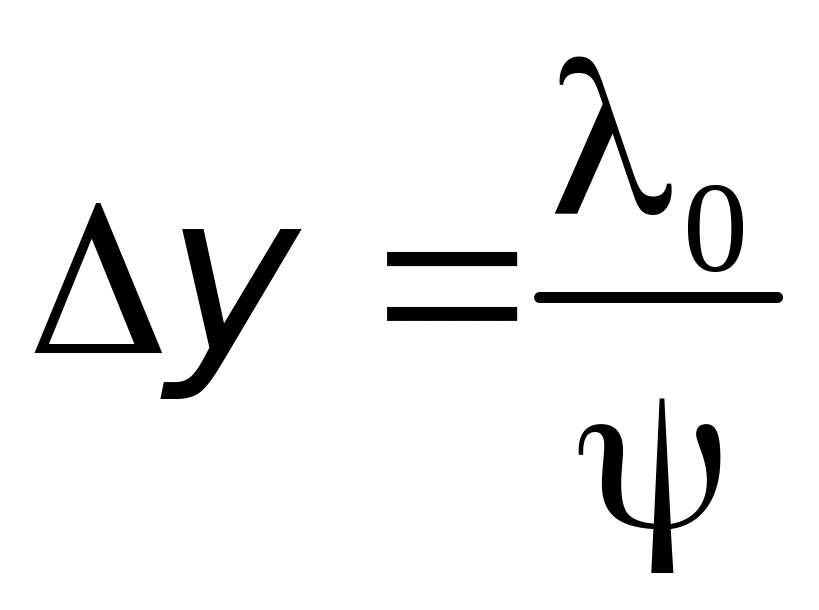. (2.8)

y

Рис. 2.7

Таким образом, ширина интерференционной полосы пропорциональна длине волны и обратно пропорциональна углу, под которым видны источники волн из центра интерференционной картины.