1. Интерференция. Условие минимума и максимума интенсивности

Интерференция света - это явление наложения в пространстве двух или нескольких когерентных световых волн, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны (свет + свет = темнота) (рис. 1.1). Для того чтобы можно было наблюдать явление интерференции необходимо, чтобы волны были когерентными. Термин когерентность означает согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Иными словами, когерентностью называют способность света давать интерференционную картину. Если интерференционная картина наблюдается, значит, источники света когерентны. Когерентность связана со структурой света: когерентный свет – это свет, структура которого близка к плоской или сферической гармонической волне.

Рис. 1.1 Рис. 1.2

Две волны будут когерентными, если они имеют одинаковые частоты ( , монохроматические волны), а сдвиг фаз колебаний является постоянной величиной, не зависящей от времени ( (временная когерентность). Это минимальное требование к источнику излучения. Для того чтобы было возможно наблюдать интерференцию излучаемых ими световых волн, источники должны быть пространственно когерентными. Об этом мы поговорим более подробно в разделе 3.5.

Пусть две волны, одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания электрического поля одинакового направления, причем до точки наблюдения одна волна прошла в среде с показателем преломления путь с фазовой скоростью , а вторая - в среде путь , с фазовой скоростью (рис. 1.2):

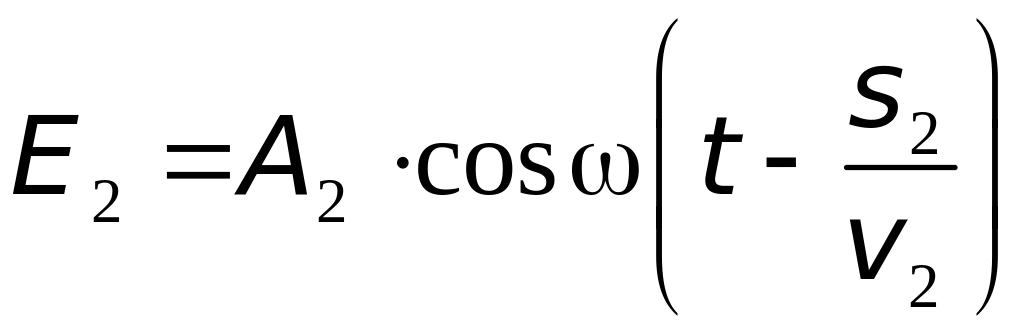, (1.1)

где и - амплитуды первой и второй волн ( ).

Из-за разного пути ( ) и разных показателей преломления ( ) волны приобретают разность фаз:

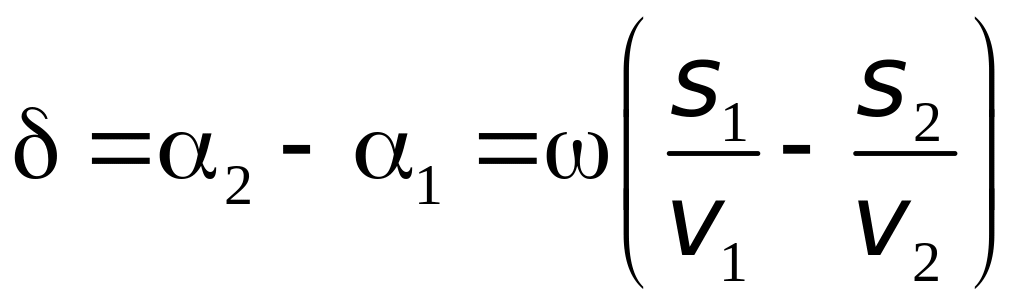, (1.2)

где и 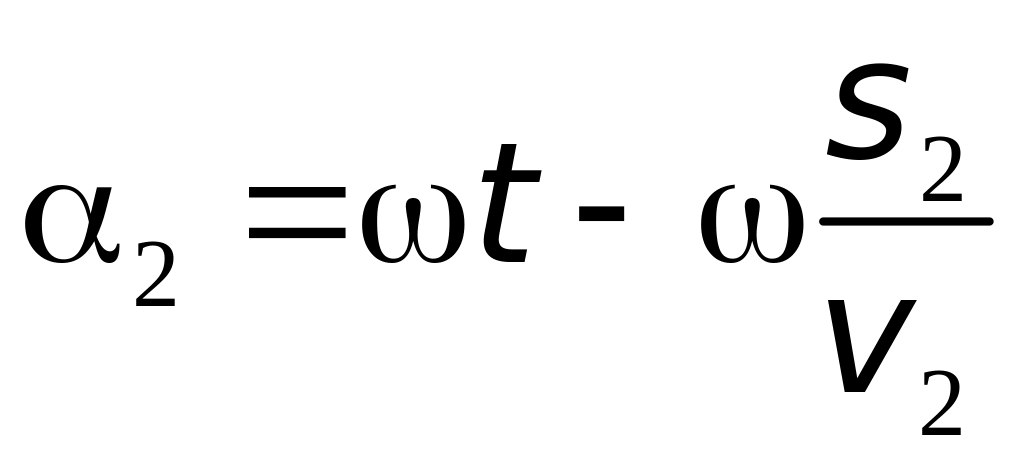- фазы первой и второй волн. Составляющая фазы , связанная с расстоянием, на которое распространяется волна, называется фазовым набегом.

Сложим амплитуды колебаний, используя правила вращающихся векторных диаграмм. Амплитуда результирующего колебания по теореме косинусов:

. (1.3)

Так как интенсивность , то интенсивность результирующей волны:

. (1.4)

Последнее выражение в (1.4) называется интерференционным членом.

Для некогерентных волн разность фаз непрерывно изменяется, поэтому среднее значение косинуса и

. (1.5)

При одинаковой интенсивности волн, когда , суммарная интенсивность

, (1.6)

т.е. для некогерентных волн имеет место закон сложения интенсивностей волн.

Для когерентных волн , т. к. имеет постоянное во времени, но своё для каждой точки пространства значение. В тех точках пространства, где >0, интенсивность будет превышать ; в тех точках, для которых < 0, интенсивность будет меньше . Это явление и называется интерференцией.

Очевидно, что максимум интенсивности будет наблюдаться в тех точках пространства, где косинус имеет максимальное значение, т.е. . При одинаковой интенсивности волн в этих точках пространства результирующая интенсивность равна:

. (1.7)

Соответственно, минимум интенсивности будет в тех точках, где , и результирующая интенсивность при

(1.8)

Отсюда следует, что максимумы интенсивности результирующей волны будут наблюдаться в тех точках пространства, где разность фаз , приобретённая волнами, будет равна чётному числу ( )

, (1.9)

а минимумы в точках пространства, где равна нечётному числу ( )

, (1.10)

где = 0, 1, 2, 3,…… - целые числа.

Более удобно для определения разности фаз пользоваться фазовым набегом, т.е. величиной, связанной с геометрическим путём и показателем преломления среды, поскольку из-за очень большой частоты колебаний напряжённостей электрического и магнитного полей световой волны (~ 10¹⁴ Гц) не существует таких приборов, которые смогли бы этот сдвиг фаз зарегистрировать. Для этого необходимо найти связь между сдвигом фаз и расстоянием, на которое перемещается фаза волны.

Найдём приобретаемую разность фаз колебаний, возбуждаемых в точке М. Из определения абсолютного показателя преломления фазовая скорость . Это выражение подставим в (1.2).

, (1.11)

где - показатель преломления среды. Произведение геометрического пути на показатель преломления среды называется оптической длиной пути

. (1.12)

Обозначим разность оптических путей через

(1.13)

и назовём оптической разностью хода.

Заменив через , (использовали ; ; - длина волны в вакууме) выражению для разности фаз можно придать вид:

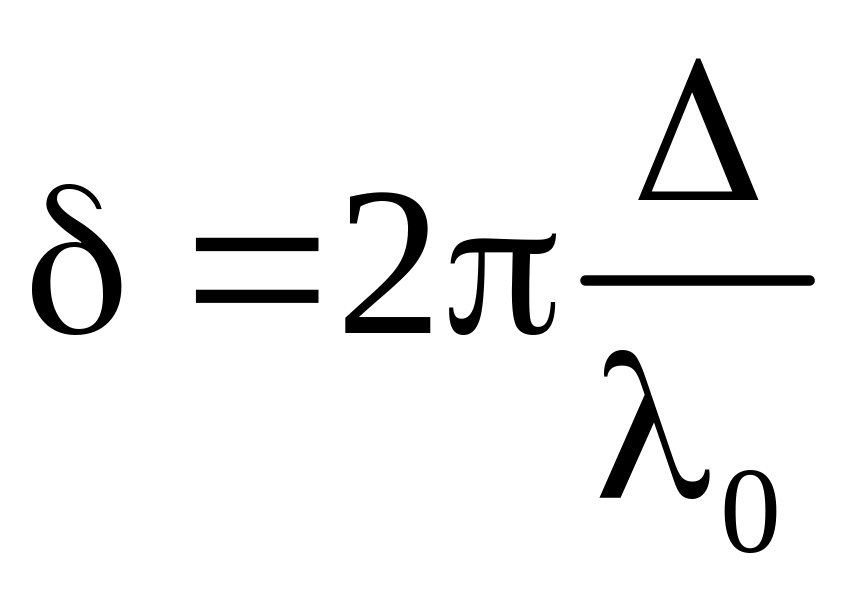. (1.14).

Формула (1.14) устанавливает связь между разностью фаз и оптической разностью хода . Разность фаз равна числу , умноженному на число длин волн в вакууме, укладывающихся в оптической разности хода.

Формулу (1.14) можно переписать также в виде:

. (1.14а)

Определение. Отношение называют порядком интерференции и обычно обозначают буквой .

Из формул (1.4), (1.9) и (1.14) следует, что максимум амплитуды результирующей волны будет в том случае, когда разность фаз складываемых волн равна чётному числу ( ):

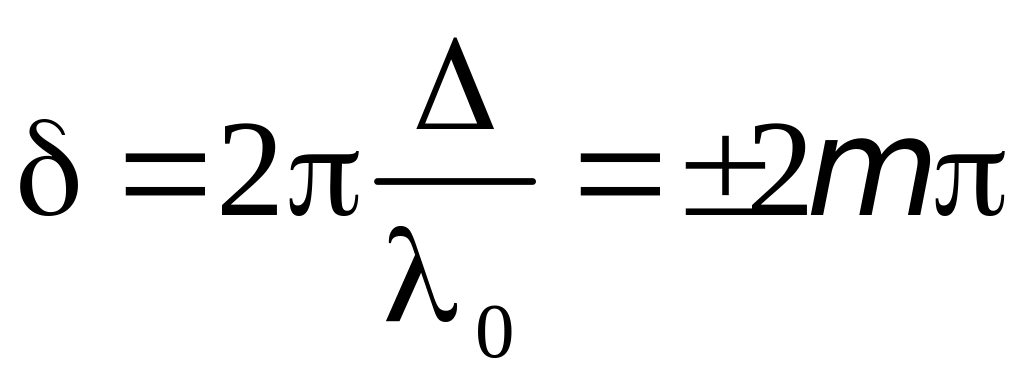. ( = 0, 1, 2, 3,……). (1.15)

Отсюда следует условие максимума:

. (1.16)

Соответственно, разность фаз , равная нечётному числу ( ),

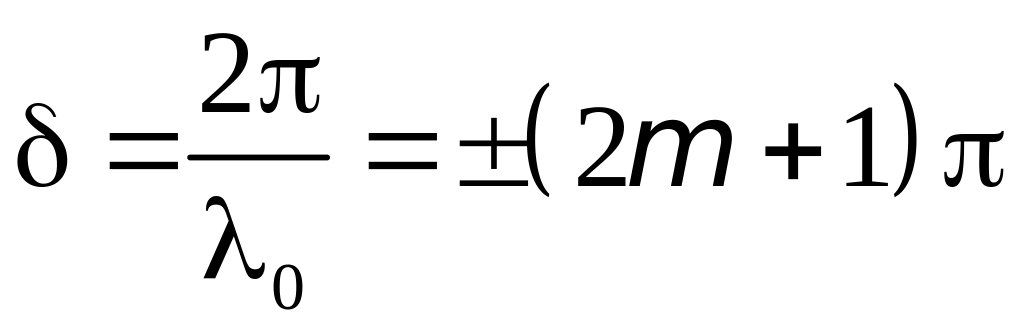(1.17)

соответствует условию минимума

. (1.18)

Таким образом, условие минимума и максимума в терминах оптической разности хода звучит следующим образом: если оптическая разность хода равна целому числу длин волн в вакууме (чётному числу полуволн), то в этой точке пространства наблюдается максимум, а если оптическая разность хода равна нечётному числу полуволн - в этой точке пространства наблюдается минимум.

Отметим, что максимумы и минимумы освещённости, наблюдаемые в интерференционных картинах, не связаны с какими-либо превращениями энергии света — в местах минимумов световая энергия не переходит в другие форма энергии, происходит лишь перераспределение светового потока, в результате чего максимумы освещённости в одних местах компенсируются минимумами в других. Закон сохранения энергии при этом не нарушается.

Излучение обычных (не лазерных) источников света представляет собой наложение огромного числа несогласованных между собой цугов волн, т.е. беспорядочные некогерентные колебания, которые не могут интерферировать. Действительно, каждая частотная компонента немонохроматического излучения создает свою интерференционную картину (полосы) в плоскости наблюдения. Эти полосы накладываются друг на друга, причем максимумы одной картины могут совпадать с минимумами другой. В результате освещённость экрана оказывается однородной, т.е. интерференция исчезает. Поэтому для наблюдения интерференции с использованием немонохроматического света приходится прибегать к различным ухищрениям: применять спектральные фильтры, располагать источники таким образом, чтобы их можно было считать точечными, и другим.

Наблюдать интерференцию света от некогерентных источников можно, если разделить излучение на два или несколько пучков, а затем свести их вместе. Хотя в каждом из пучков за время наблюдения фазовые соотношения между цугами хаотически изменяются, эти изменения одинаковы в разных пучках. Интерференционная картина будет наблюдаться, если разность хода между пучками не превышает длины отдельного цуга.