2.3. Задачи по трехфазным преобразователям

Задача 2.25. Определить допустимые значения выпрямлен­ного напряжения, тока и мощности нагрузки, питаемой выпрямите­лем со схемой соединений ЗФ1НЗП, если нагрузка состоит только из резистора, допустимое среднее значение тока вентиля 200 А, а допустимое максимальное значение повторяющегося обратного напряжения на диоде £/_Об_Р.манс=700 В. Выпрямитель не содержит последовательно или параллельно соединенных диодов. Сеть, транс­форматор и диоды идеальные.

Решение. Максимальное обратное напряжение диодов свя­зано с действующим значением фазного напряжения U_s вентиль­ной обмотки трансформатора соотношением

^об_Р.ма_Кс = /3"^:1^/27^.

U

р. макс

o6p.

700

sin-y* VT-285,5-— si

Наибольшее допустимое значение выпрямленного напряжения Р

Ud = V%~U_S - ■ _эт ^в*^м з

Наибольший допустимый ток нагрузки

Id=pI_Pt.c_v=3 -200=600 А,

Наибольшая мощность нагрузки

Pd=IdU_d=600-334,5-200,7-10^й Вт=200,7 кВт.

Задача 2.26. Неуправляемый выпрямитель со схемой соеди­нений ЗФ1НЗ.П работает на активную нагрузку. В одной из фаз сработал предохранитель. Построить кривую выпрямленного тока

и найти его среднее значение (рис. 2.61). Найти средние значения токов вентилей в неповрежденных фазах. Вентили и трансформа­тор идеальные. Дано: jRd=-l Ом, t/_s=100 В.

Решение. Кривая выпрямленного напряжения показана на рис 2.61. Кривая выпрямленного тока подобна. Для этих кривых получаем:

5*/6

и*-

о

Щ№ (__cos^l₊₁)_=84B.

U_d 84 / _ / ^-= 40 А

'Д«ср 'Д2СР— 2

Задача 2.27. Преобразователь cq схемой соединений ЗФЩЗП работает на активную нагрузку, i?d=40 Ом. Действующее значение фазного напряжения вентильных обмоток трансформатора U_s= =220 В, угол управления а=60°. Построить кривую тока нагрузки. Определить среднее значение тока нагрузки, а также среднее и действующее значения тока тиристора.

Решение. Кривая тока нагрузки показана на рис. 2.62. Про­водимость прерывистая, следовательно,

1С

^Ud — "h \ У^^и*&* <Й«=1£ V2~~220 [-cos tof]l_j2 = 148,5 B;,

«с/2

V_d 148,5 _№ .

'T.Cp— 3 3 —

(l/"2 c/ssintor)²^

= 11 A.

3 а д,а ч a 2.28. Для схемы, показанной на рис. 2.63, определить средние значения токов нагрузки и вентиля. Построить кривую тока U. Дано: £Л=220 В, L_d=l мГн, а=90°, /=50 Гц. Тиристоры иде­альные.

l

Рис. 2.62. Кривая выпрямлен­ного напряжения (к зада­че 2.27).

a

Рис 2.63. Схема выпрямителя (задача 2.28).

Решение. Кривые тока и напряжения показаны на рис 2.64. Уравнение

La -^-=V2 U_ssiutat с начальным условием id=0 при Ы=а' имеет решение:

yrv_s

td ⁼ —ы7_й— (^{cos а}' ~~ ^{cos ы}) '•

а =120°.

Преобразователь работает на границе между непрерывной и прерывис»ой проводимостями. Среднее значение тока нагрузки

ВЫКЛ

Щр

_{1 '•'}

toL_rf

■х

' , V2V_sp

A (cos о' — cos Ш) Ш = —Щ— К^а'выкл — «) cos а' +

+ sin а' — ^по'вцад].

П

2п 314-10-³

одставив численные значения, получим: 3 VT 220

LV з з ; ^cos з ^x

+ sin-|L-_sinJ!l]-326A.

Среднее значение ;тока тиристора

/_тср = _и 108,66 А.

Рис. 2.64. Диаграммы токов и Рис. 2.65. Схема к задаче 2.30. напряжений (к задаче 2.28).

Задача 2.29. Управляемый преобразователь со схемой со­единений ЗФ1НЗП работает на нагрузку, состоящую из последова­тельно соединенных резистора и реактора. Определить значение индуктивности La в цепи постоянного тока, при которой преобра­зователь работает на границе между непрерывной и прерывистой проводимости ми, при а=>80°. Активное сопротивление нагрузки R_d— =4 Ом. Все вентили идеальные.

Решение. Для решения задачи может быть использован график, представленный на рис. 2.13. В данном случае

й==0; а' = а + -^—^-=80 + 90 — 60 — 110^е.

Следовательно, фазный угол выключения при работе на границе между непрерывной и прерывистой проводимостями будет:

2я

«выкл -= а' + — = 110 + 120 = 230°.

Из графика видно, что при этих углах cosq>=0,4. Из соотно­шения

ш

находим:

—

1 =

0> f COS"* «

1=29,2 мГн.

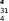¥ 314 r 0,4^:

Задача 2.30. Для схемы, показанной на рис. 2.65, построить кривые выпрямленного напряжения и&, токов вентильных обмоток

идеального преобразовательно- _и го трансформатора и тока

шунтирующего диода. Угол управления а=60°.

Определить действующее и среднее значения токов вен­тильных обмоток трансформа­тора и шунтирующего диода и среднее значение выпрямленно­го напряжения для L%—220 В, /==50 Гц, i?d=10 Ом, Ld^oo. Определить, при каком угле управления проводимость ста­новится прерывистой, если шун­тирующий диод До удален из схемы, a Ld=73 мГи.

Решение. Кривые тока и напряжения показаны на рис. 2.66. Здесь а'=я:/2. При наличии шунтирующего диода

О. вы к л — ЗТ.

Среднее значение напря­жения на нагрузке

Ud==~2H \ y^r^U_ssiniatd^t=-^-V2 U_s = -^rV2 -220= 148,5 В.

и/2

Среднее значение тока нагрузки

/ _ ^U* ¹⁴⁸'⁵ ~ Щ ~ 10

= 14,85А.

С

-=14,85-

-=3,71 А.

реднее значение тока вентильной обмотки трансформатора

.

2тс

л — (л/2)

^5ср — Id

Действующее значение тока вентильной обмотки трансформа-

тора

(

- = 14,85

гс/2) _14,85_

2л ^{1 ,w} V 2к

Среднее значение тока шунтирующего диода

7,43 А.

^д.ср — Id

(

2г. 3

ГС 7С \

/ (л/6) I

Действующее значение тока шунтирующего диода , , -/ (л/6) _14.8

(2^/3)

Если шунтирующий диод отсутствует и L_d=7S мГн, из тас 2 1Я при" а = 0, р = Ъ и "

10

cosy =

=0,4

для границы между непрерывной и прерывистой проводимостями находим а'=11Г, т. е. искомый угол управления .а=о/—30=81°.

Задача 2.31. Управляемый идеальный преобразователь со схе­мой соединений ЗФШЗП работает на нагрузку, состоящую из после­довательно соединенных активно­го сопротивления \Rd~\0 Ом и индуктивности Ld^oo. Действую­щее значение фазного напряжения вентильной обмотки трансформато­ра U_s—220 В, угол управления а=60°. Построить кривые выпрям­ленного напряжения и тока тири­стора. Определить среднее и дей­ствующее значения тока нагрузки и тока тиристора.

Решение. Кривые показаны на рис. 2.67.

Среднее значение напряжения

„ cos а = V2 - 200 ~sin-J- cos-?- = 117B. Р те «5 6

Среднее значение тока

.11,7 А.

Среднее значение тока тиристора

'т.ср •

р з

Действующее значение тока тиристора

Задача 2.32. Неуправляемый преобразователь со схемой со­единений ЗФШЗП работает на активную нагрузку через сглаживаю­щий реактор с индуктивностью Ld~°°- Среднее значение выпрям­ленного тока /d=100 А. Напряжение вентильной обмотки транс­форматора Us—220 В. Реактивное сопротивление коммутации Xj== =0,05 Ом. Определить среднее значение выпрямленного напряжения и действующее значение тока вентильной обмотки.

Решение. С учетом коммутации выпрямленное напряжение равно:

жГ— Р я 3

U_d = У 2 U_s — sin — — ₀ =V 2 220 — sin 60^е —

_ 3-100.0,05 __oqfiR 2гс

Для того чтобы определить фазный ток, требуется зиать угол коммутации. Так как

ВД| 100-0,05 cosy = 1 ^ =1 ——— -f=^==0,9815s

У2 U_s sin |/"2 - 220KL

то v=arccos 0,9815=10°.

Из графиков на рис. 2.15 находим поправочный коэффициент:

V\ — /ЯГ? (a, _Y) = Kl—/ЯР(0, 10) = 0,99,

следовательно, действующее значение тока будет равно:

/_{rf Л} 100

/s=--j^T^rl-3W(a, у) =y=0,99 = 57,2 А.

Задача 2.33. Неуправляемый преобразователь со схемой со­единений ЗФ1НЗП работает иа нагрузку, состоящую из последова­тельно соединенных реактора с индуктивностью L<j и резистора с сопротивлением Rd.

'Путем измерений получены следующие данные: напряжение на резисторе Ud=2l7 В, фазное напряжение вентильных обмоток трансформатора U_s=l§0 В, f=50 Гц, ток вентильной обмотки /_в= = 500 А, угол коммутации 6°.

Определить активное сопротивление нагрузки Rd и индуктив­ность трансформатора L_T. Активное сопротивление обмоток преоб­разовательного трансформатора и падение напряжения на диодах пренебрежимо малы.

Решение. Соотношение между током вентильной обмотки трансформатора и средним значением тока нагрузки определяется из уравнения

S

= yj=-V\~_P4?{«, _Т) =^У1-ЗЧР(0, 16) .

Поправочный коэффициент на угол коммутации находится из графиков рис. 2.15:

|Л — ЗФ (0, 16) = 0,985,

следовательно,

Уъ~1₈ /Г-500

1_а = -^s п пёк ="879,2 А.

d У\ — ЗЧР(0, 16) °.985

Активное сопротивление нагрузки

_^=-^=|й⁼⁰-^{2478 Ом}-

Реактивное сопротивление коммутации находится из уравне-

НИЯ'

2тс

следующим образом:

2«

2п

я 3

8

314

79,2 *Y 0,0103

■т 2nf

*4 -217,9

= 0,0103 Ом

Задача 2.34. Определить средние значения и форму кри­вой тока нагрузки н тока, про­ходящего через тиристор пре­образователя со схемой соеди­нений ЗФ1НЗП, показанной на рис. 2.68.

Трансформатор и вентили идеальные. Дано: #_s = 100 В, Fa — 70,7 В, /?<* = 1 Ом, а =-60°.

Решение. Как показано на рис. 2.69, при заданных значениях Еа и а проводи­мость будет прерывистой.

Из выражения

i , sin а _ВЬ1кл — 2U

70,7

-КГ. loo ^=0,5

с

Рис. 2.69. Диаграммы выпрямленных напря­жений и токов (к за­даче 2.34).

5—9

ледует, что

а среднее значение выходного напряжения равно:

V_d - VTU_S -jf- [sin (а_ВЫКл --у)-sin (а - ~)j= 2гс

^~ ("выкл — ^а)

2тс

Подставив численные значения, получим:

£/_d=94,05 В. Искомые значения токов равны:

Ud — Ed 94,05 — 70,7 и=—Щ - 1 =23,35 А;

I т.ср ⁼⁼ ~g ~7,78 А.

Задача 2.35. Двигатель постоянного тока возвращает энер­гию в сеть через преобразователь со схемой соединений ЗФ1НЗП, работающий в инверторном режиме. Характеристики двигателя: E_d= =220 В, Rd=2 Ом, Ld^oo. Характеристики трансформатора: U_a— =220 В, /=50 Гц, L_T=1 мГн. Вентили идеальные. Найти угол управ­ления, при котором отдаваемая двигателем мощность P,i=EdId равна 5 кВт. Найти действующее значение тока вентильной обмот­ки трансформатора.

Решение. Выпрямленный ток равен:

Р_л 5-Ю^{3 Id} — E_d ⁼ 220 =²²»^{75 А}-

Падение напряжения на стороне постоянного тока

Id \*й + j⁼ 22,75 (2 -f- 0,15) = 46,7 В.

Это падение напряжения уравновешивается напряжением Е&~\--\-Ud> поэтому

£/_d=46,7—£^=46,7—220=—173,3 В. Угол управления может быть определен из соотношения

Vd = V 2~U_S -~- sin -~ cos о = К2~-200 — sin -jj- cos а = 257,4 cos о, т. е.

a = arccos^-257^J=132,3 . Угол опережения

Р= 180—а=47,7°.

Для инверторного режима угол коммутации у находится из уравнения

cos (р — Y) = cosp+ — —

Vi u_s sin y

Подставив численные значения, получим: Y=2,5°.

Из графиков рис. 2.15 и уравнения (2.7) поправочный коэф­фициент на угол коммутации будет равен 0,998, следовательно,

Id 22,75

0,998 = -7^-0,998= 13,2 А.

Задача 2.36. Управляемый преобразователь со схемой со­единений ЗФ1НЗП работает на нагрузку (рис. 2.70,а). Угол управ­ления а=150°. Построить кривые падения напряжения на нагруз­ке и тока нагрузки. Найти среднее значение тока нагрузки. Транс­форматор и вентили идеальные. Дано: [/,=100 В, R_d—l Ом, Ld=<x>, £_d=200 В.

Рис. 2.70. Схема выпрямителя и диаграммы к задаче 2.36.

Решение. Кривые напряжения и тока приведены на рис. 2.70,6. Уравнение для средних значений напряжений в цепи постоянного тока:

U_d-\-E_d—F_dR_d=0. Среднее значение выпрямленного напряжения Uл = VTU_S — sin — cos а = VT-100 -|-sin 4- cos 150=—101, ljB.

к p it о

Среднее значение тока i_d

Задача 2.37. Неуправляемый выпрямитель со схемой со- единений ЗФ1НЗП работает на нагрузку, состоящую из последо- вательно соединенных источника противо-ЭДС Ed—90 В, реактора с индуктивностью L_d^oo и резистора с сопротивлением R_d, зна- чение которого неизвестно. Падение напряжения на диодах выпря- мителя Лс/д._Ср=1 В на ветвь. Значение индуктивности рассеяния трансформатора неизвестно. Фазное напряжение вентильной обмот- ки t/_s=l 00 -В. Значение тока одной вентильной обмотки трансфор- матора, измеренное при помощи электродинамического измеритель- ного прибора, равно 10 А, а значение, полученное при помощи маг- нитоэлектрического прибора, равно 6 А. Найти R_d- ' .

Решение. Задача может быть решена с помощью графиков рис. 2.15.

Ток нагрузки определяется по среднему значению тока вен­тильной обмотки:

I_d=pl_{s ср}=3-6='18 А.

По действующему значению тока вентильной обмотки можно определить поправочный коэффициент для угла коммутации:

Vl — p4?{0, y)^¹^-^ ^Ю?8^~ ⁼⁰'96; ЧР(0, у) = 0,026.

Из графиков находим, что этому значению поправочного ко­эффициента соответствует угол коммутации у=36°. Зная это, Rd можно найти из уравнения равновесия напряжений на стороне по­стоянного тока, которое после преобразований приводится к виду

Rd= j = 18 =0,83 Ом.

З

Рис 2.71. Схема вы­прямителя к зада­че 2.38.

адача 2.38. Выпрямитель со схемой соединений, показан­ной на рис. 2.71, питается от трехфазного стержневого трансфор­матора. Построить кривую и найти среднее значение выпрямлен­ного напряжения. Найти действующие значения токов в сетевых об­мотках трансформатора при условии, что /?d = 13,5 Ом, L_d«оо,

l/_s=100 В, угол управления управляемого преобразователя а=60°, числа витков обмогок трансформатора Wp — uu.,.

Решение. Так как Ld^z ^оо, ток, проходящий через нагрузку при двух последова­тельно соединенных выпрями­телях, идеально сглажен, т. е. оба выпрямителя находятся в состоянии непрерывной прово­димости. В этом случае ре­зультирующее выпрямленное напряжение будет равно сумме выходных напряжений этих двух выпрямителей (рис. 2.72,0, б).

Среднее значение выпрям­ленного напряжения определя­ется из рис. 2.27,а. Для этого следует просуммировать вы­ходные напряжения двух вы­прямителей со схемами соеди­нений 1Ф2Н2П, работающих при углах управления 0° и 60° соответственно:

г~ sin (к/2) ^ _ч ЗУ 2 .

U_A = V* Vs _п/У (l + cos60°)== ——U_s.

Из рис. 2.72,6 видно, что результирующее выпрямленное на­пряжение такое же, как и выходное напряжение однофазного двух-пульсного выпрямителя с углом управления 30°, питаемого напря­жением Уъ U_s:

Подсчитав численные значения, получим: £/d=135 В.

Токи вентильных обмоток фаз 2 и 3 имеют прямоугольную фор­му с амплитудой Id, в то время как ток вентильной обмотки / ра­вен нулю (рис. 2.72,е, г, д).

Обозначив через F₀ некомпенсированную (остаточную) МДС стержней трансформатора, из уравнений для магнитной цепи при w_s—w_p=w получим:

Так как

ip i~\-ip2—"-рз—0,

то

F₀=—w (irt-f-its) /3;

ipi=—1 / 3/_S2— 1 /3£s3»

ip2⁼⁼2/3/s2—1/3^631

^рз=2/3/бз—1/3£₈2-Кривые токов сетевых обмоток и нескомпеисироваиной МДС показаны на рис. 2.73. Выпрямленный ток

Ud 135

Действующие значения токов сетевых обмоток: /р₂ = Iрг — "з~ 7^ = 3,33 А;

= —/_й = 6,6б А.

Задача 2.39. Управляемый преобразователь со схемой со­единений ЗФ1НЗП, имеющей шунтирующий диод, работает на на­грузку, состоящую из последовательно соединенных резистора с со­противлением Rd—2, Ом и реактора с индуктивностью Ld~°°. Опре­делить среднее значение тока нагрузки и углы коммутации при ус­ловии, что фазное напряжение вентильной обмотки преобразова­тельного трансформатора U_s—220 В, реактивное сопротивление коммутации Xj=0,l Ом, угол управления а=60°. Полупроводнико­вые вентили идеальные, а индуктивность цепи шунтирующего диода равна нулю.

Решение. Предположим, что в течение определенных перио­дов времени ни по одной из вентильных обмоток не протекает ток. При таком предположении «кривая напряжения «d приобретает вид, как показано на рис 2.74,0, а кривые фазных токов и тока шун­тирующего диода — как показано на рис. 2.74,6. В этом случае вен-

10

х

zx

cut

зх

cot

^_

wt

_ъ

Рис. 2.73. Диаграммы токов сетевых обмоток и неском-пенеировашюй МДС транс-эматора (к задаче 2.38).

тиль каждой фазы всегда коммутирует с шунтирующим диодом. Так как напряжение щ равно нулю каждый раз, когда шунти­рующий диод находится в проводящем состоянии, то во время каж­дом коммутации фазные напряжения поочередно прикладываются к реактивному сопротивлению контура коммутации.

В соответствии с рис. 2.74,а среднее значение выпрямленного напряжения равно:

J ^2 Vs sin ШЫ = ^ У2 U_s [1 -f cos (о + _Yl)].

3 ^а+Тх

Угол коммутации Yi определим из уравнения -г dl_sl

Это дифференциальное уравнение с начальным условием t"_ei=0 при (i)t=a имеет решение

YTu_s

i_sl = у (cos а — cos со/),

а так как l_sl = Ja при (of = а-|- у„ то оно приобретает вид:

YYu_s

*d = у [^{cos а} — ^cos (^а + Yi)] •

Кроме того,

U_d з УТи₅

Следовательно,

а + yi = arccos ₂^_d+3^ l^cOSa"~~2^~R_d~)

2n2

= ^arccos2^2T3-

Yi=62,28—a=62,28—60=2,28°.

Зная угол коммутации уь находим среднее значение тока:

тЛ2~С/_я

/_d = ^- [cos a — cos (a -f Yi)J =

=^²₀'²²° (cos 60° — cos 62,28°) = 108,57 A.

Для определения угла коммутации у₂ используем дифферен­циальное уравнение

u_sl = У2 U_s sin (of = Х_л - jg,

которое с начальным условием isi=0 при а>*=ет-ру2 имеет решение *£i = — %^V* (cos Y₂ + cos cor).

Поскольку i_sl = Id при = гс, то V2U_S

lu — — -~x (cos y₂ + COSir).

Так как

Id =

u_d _ з V\ u_s

R_d 2n R_d

[l + cos(o-f-Y,)].

TO

[

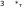
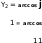
2я 3

2d 0,1

1+cos (« + Yi)]/^e -(1 + cos 62,28) J. = 15,2.

2n 2

Полученные результаты подтверждают исходное предположе­ние.

Задача 2.40. Преобразователь имеет схему соединений ЗФ1НЗП (рис. 2.75), одна из фаз сетевой обмотки стержневого

трансформатора отключается. Транс­форматор идеальный. Числа витков сетевой и вентильной обмоток w_v и w_s. Как изменится значение выпрям­ленного напряжения в результате от­ключения, если сетевые обмотки со­единены в звезду, а нейтраль: а) вы­ведена, б) изолирована.

Р

и а_р2 =

Ир, = W

ешение, а) Фазные напряже­ния сетевой обмотки трансформатора iip\ и u_V2 фиксированы, поэтому по уравнениям

dф_l

» . dt

определяют магнитные потоки <Di и Ф₂ в фазах 1 и 2 трансформатора. Из уравнения для потоков

ф₃=—ФН-Ф2,

такого же, как и для симметричного трехфазного случая, следует, что напряжение «₈з при отключении фазы 3 не изменяется.

При выключенных вентилях в фазах 1 к 2 результирующие МДС в сердечниках трансформатора равны нулю.

При включении вентиля в фазе 3 уравнения равновесий МДС принимают вид:

ipiWp—/_Р2сУр=0; ip\t&)p—i_s 3^8=0,

и, следовательно,

1р\ — ^lpz — — ^ът _Wp "

Таким образом, каждый сердечник трансформатора намагни­чивается односторонне в соответствии с полной нагрузкой велтиль-ной обмотки, но, так как предполагается, что трансформатор иде­альный, это не влияет на его работу. Таким образом, выпрямлен­ное напряжение остается неизмененным.

б\ Полагая, что трансформатор идеальный и обращаясь к рис. 2.76, получаем уравнения при отсутствии нагрузки:

U л1—^ир\—^ир2,

Ф1-И>Н-Фз=о.

Задача, сформулированная таким образом, является некоррект­ной. Тем не менее она может быть решена, если допустить, что маг­нитная проницаемость р, материала сердечников конечна. Для про­стоты магнитным сопротивлением ярма можно пренебречь. Если / — длина и S — площадь поперечного сечения сердечника, то

H\l—H2l^=zWpip\—wpip2\

H_tl—Нzl=w_pipi; Ф1+ФН-Фз=0;

O_z=p,H₃S.

Решением этой системы уравнений является <Di =—Ф₂; Фз=0,

т. е.

tip (= Upzl &рз=0,

и, следовательно,

Up\ — 2 ' ^pz — 2

Схема соединений при отключении одной фазы преобразуется в схему типа 1Ф1Н2П. Выходное напряжение трехфазной схемы равно:

При отключении одной фазы уравнение принимает вид:

,_ 2 гс -_r—VT 2 гс V_d = V2U₈— sin_T=K2 _i/_e_»i — _e

т. е. напряжение снижается на 33,3%.

Рис 2.76. Схема соединений Рис. 2.77. Схема выпрямителя к задаче 2.40. к задаче 2.41.

Задача 2.41. Для схемы, показанной на рис. 2.77, определить среднее значение напряжения и тока на стороне постоянного тока, угол коммутации и токи вентильных обмоток преобразовательного трансформатора, если: а) а=30° и Е<*=Н50 В; б) а=150° и E_d— -—.150 в.

Индуктивность рассеяния трансформатора =1 мГи, Us— «=100 В, fs=50 Гц. Цепь постоянного тока имеет резистор с со­противлением R_d=\ Ом и реактор с индуктивностью Ld^oo, со­единенные последовательно с противо-ЭДС Е&.

Решение. Напряжение и ток на стороне постоянного тока могут быть определены с помощью уравнений

г— р к JrfCoLy _w

U_d = I_dRd + Ed,

из которых получаем:

' ,r— Р ^

У 2 U_s — sin — cos а

т.

ld=

*« + -5Г

а) Для а=30° кривые напряжения и тока на стороне постоян­ного тока и тока вентильной обмотки в фазе 1 показаны на рис. 2.78. Средние значения тока и напряжения:

-_г 3 п п _,

У 2 -100 — sin -g- cos ——50

Id = "зМ-Ю-'-З = 44,8 A;

5+ 2*

U_d = 44,8-1 +50 = 94,8 B.

У

/_dcoZ,_T

гол коммутации можно вычислить с помощью соотношения cos (a -f- y) = cos а —

V2 U_s sin -y Подставив численные значения, получим:

4

V2 -100 sin ~y *

4,8.314.10-»

cos (30^е -f _Y) = cos 30^#

откуда 7=11,15°.

Ч ос

Действующее значение тока вентильной обмотки равно:

Значение функции ^(а, у) может быть получено из кривых на рис. 2.15, для чего надо сначала вычислить угол коммутации Yo, который будет при угле управления а=0°. В соответствии с ус­ловиями задачи

cosyo= 1

=1 44,8.314-Ю-³

K2t7_ssin— V2 -lOOsin-^-

s р 3

откуда Yo=27,7°.

Из рис. 2.15 получаем ^(а, y^⁰*⁰*^, следовательно,

I_s=yUV\— 3-0,0115 = 25,4 А.

б) Для .а=150° требуемые кривые представлены на рис. 2.79. Средние значения тока и напряжения на стороне постоянного тока:

_,-— _я 3 г. Ьъ V2 -100— sin -5- cos

■150

=

fd =

43 А;

1 + (314-Ю-³-3)/2тс

£Лг=43-1—150=—107 В. Угол коммутации находим из уравнения

43-314-10-⁸

c

sin

os (150° +y) = cos 150° —

V~2 -10 si

т. е. <y=17,7°. / При a=0°

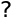Yo = arccos / 1 —

43-314-10-³

V~2 -100 sin

=27,3°.

Из рис. 2.15: ЧЧ-а, у) =0,0207. Действующее значение тока вентильной обмотки

43 ,_А

f_s = yr-Vi —3-0,0207 = 24 А.

Задача 2.42. Трехфазный неуправляемый преобразователь с мостовой схемой соединений (рис. 2.80) работает на нагрузку, состоящую из последовательно соединенных резистора с сопротив­

лением R_d к реактора с индук­тивностью L_d. Построить кри­вые выпрямленного напряже­ния, тока диода и фазного то­ка. Определить средние и дей­ствующие значения тока диода и фазного тока, а также угол коммутации при условии, что l/_s=220 В, Х_т=0,3 Ом, R_d = = 5 Ом, Ld~oo. Диоды идеаль­ные, а активное сопротивление трансформатора пренебрежимо мало.

Решение. Кривые напря­жений и токов представлены на рис. 2.81*. Среднее значение выпрямленного напряжения равно:

2 2/ jX

Vd = IdRd = 2 VTU_S — sin-|—-j—щ=2,Z4U_S

отсюда

ld =

2.34LL

3X_y

Rd +

2,34-220

-=97,5 A

U_d = 97,5-5 = 487,5 B.

Зависимость cos у = 1

l_dX.

V~2 U_s sin

= 1

97,5-0,3 '2-220-0,866

=0,891

дает угол коммутации

Y = arccos 0,891 =27°. Среднее значение тока диода

^д.ср —'

97,5 -=—=32.5 А.

Действующее значение тока диода

/

* Напряжение u_d должно отсчитываться между нижней и верх­ней жирными кривыми, указывающими соответственно напряжения Отрицательного и -положительного полюсов выпрямителя относитель­но нулевой точки вторичной обмотки трансформатора. (Прим. ред.)

д = р="^1-ЗФ(а, у).

Из графиков рис.. 2.15 f 1 — ЗФ (0,27) = 0,972, следовательно, 97 5

/_д = г-—т 0,972 = 54,6 а. V 3

Среднее значение фазного тока вентильной обмотки

Is ср⁼⁼0,

а его действующее значение

/₅ = К2~/_д = 1^/"2".546 = 77,2 а.

Задача 2.43. Определить средние значения выпрямленного напряжения и максимальные значения обратного напряжения на вентиле выпрямителя в схемах, показанных на рис. 2.82,а, б, при условии, что проводимость непрерывна.

Рис. 2.82. Схемы к задаче 2.43.

Решение. Обе схемы соединений могут быть разделены на две отдельные коммутационные группы / и //, выходные напря­жения которых суммируются. Таким образом, выпрямленное на­пряжение в обоих случаях одинаково:

V_d = 2 VTV_S — sin -^-=2,34<V

Одинаковы и максимальные значения обратного напряжения на вентиле:

^обр.макс = VT VZ~U₈.

Задача 2.44. Управляемый выпрямитель со схемой соеди­нений ЗФ2И6П питает резистор с сопротивлением Rd=20 Ом (рис. 2.83). Действующее значение фазного напряжения вентильной обмотки идеального преобразовательного трансформатора со схе­мой соединений звезда — звезда U_a—\00 В. Угол управления а=60°. Ширина управляющих импульсов 65°. Построить кривые выпрям­ленного напряжения и тока тиристора. Вычислить среднее значение выпрямленного напряжения и среднее значение тока тиристора.

Р

* См. примечание к рис. 2.81 в задаче 2.42.

ешение. Кривые выпрямленного напряжения «д и тока ти­ристора 7\ показаны на рис. 2.84*. Выпрямитель работает на гра­нице между непрерывной и прерывистой яроводимостями. Выпрям­ленный ток спадает до нуля при /каждой коммутации, а тириетор, имеющий угол управления а, выключается. В этих условиях для непрерывной работы выпрямителя необходимо, чтобы либо управ­ляющие импульсы повторялись через интервал 60°, либо они были шире 60°. Импульс шириной 65° удовлетворяет последнему усло­вию.

иа

Рис. 2.83. Схема выпрями- Рис. 2.84. Диаграммы напряжений

теля к задаче 2.44. выпрямителя и тока тиристора

(к задаче 2.44).

Среднее значение выпрямленного напряжения .

U_d=2 VTU_S ~ sin — cos а = 2 УТ-100 — sin -у cos 60° = 117 В. Среднее значение тока нагрузки

U_d 117 . /_rf = -^_r=-_ir-=5,85A.

Среднее значение тока тиристора

1_А 5,85 _Л .

/ U 1 qk Д

* Т.Ср g — g —1гд.«Ы -rv-

Задача 2.45. Определить среднее значение тока, прохо­дящего через активную нагрузку #d='10 Ом после срабатывания предохранителя в одном из плеч трехфазного мостового управляе­мого выпрямителя (рис. 2.85). Напряжение вентильной обмотки трансформатора t7_s=100 В, угол управления о=30°, ширина им­пульса управления 120°.

Р

* См. примечание к рис. 2.81 в задаче 2.42.

ешение. Кривые выпрямленного напряжения представлены на рис. 2.86*. Широкий импульс управления обеспечивает возмож­ность начала проводимости сразу же после включения тиристора, у которого «атод соединен с фазой J, так как тиристор, у кото­рого анод соединен с фазой 2, в этот момент еще получает управ­ляющий импульс. Площадь под кривой напряжения, которая ха­рактеризует снижение выпрямленного напряжения, обусловленное разрывом в одном из плеч моста, показана горизонтальной штри­ховкой.. Среднее значение напряжения может быть вычислено, на-

пример, следующим образом:

2 1

Щ = "з" Udio cos a -f- -^7-

V~3 V~2 f/c sin ШЫ =

, Я

6

sin-3-

=-3- 2 У 2 11 _s -^73- cos 30° -f —^ U_s {-cos тс -f cos—)=

= 135,2 + 5,2 = 140,4 B.

В выражении для Ud первое слагаемое соответствует верти­кально заштрихованной площади, а второе — площади зачерненного участка.

Зная среднее значение выпрямленного напряжения, находим:

U_d 140,4 /,= -^-=-Т0- = Н,04А.

Задача 2.46. Одна из фаз трехфазного неуправляемого мо­стового выпрямителя отключена (рис. 2.87).

а) Какого типа схема соединений получится в результате?

б) На сколько снизится выпрямленное напряжение?

в) Как это повлияет на спектр гармоник выпрямленного на- пряжения?

Решение, а) После отключения фазы С диоды Д₃ и Д_с стали бы проводить ток только в том случае, когда u_d меньше нуля. В неуправляемом выпрямителе это невозможно. Соответственно' ветвью Дз—Дс можно пренебречь. В результате получаем схему соединений 1Ф2Н2П (однофазный мост).

б) Среднее значение выпрямленного напряжения в первона­чальной схеме соединений ЗФ2Н6П

sin-g-=2,34i7_s.

Среднее значение выпрямленного напряжения б получившейся схеме соединений 1Ф2Н2П

и._иь = VTVTU_S sin-тг = 1,56U_S.

Таким образом, изменение выпрямленного напряжения со­ставляет:

и

U

сНФ — ^Ud3<P 1,56 — 2,34

2,34

100*= — 33,3%.

в) Спектр гармоник: в первоначальной схеме ЗФ2Н6П «=ср= =ггс-6=6, 12, 18, 24; в получившейся схеме 1Ф2Н2П я=ср=с-2=2„ 4, 6, 8, 10 ...

A Q В Q QC

II П

Задача 2.47. Трехфазный управляемый мостовой выпрями­тель работает на нагрузку, состоящую из последовательно соединен­ных резистора с сопротивлением /^=2,25 Ом и реактора с индук­тивностью Ld=oo при t7_s=H0 В и 7d=100 А. Определить среднее значение выпрямленного напряжения и ток нагрузки после сраба­тывания предохранителя в фазе С (рис 2.87) при условии, что устройство управления не сместит управляющие импульсы.

Решение. Угол управления может быть вычислен из условий нормальной работы. Уравнения для напряжений:

L/_d=2,34t7_s cos а;

U_d=J_dRd.

6—9

81

Решая эти уравнения относительно угла управления, полу­чаем:

а = arccos

2,34с/о

arccos

100.2-225 2,34-110

=30°.

Ha рис. 2.88 показаны потенциалы положительного (сплошные линии) и отрицательного (пунктирные линии) полюсов выпрями­теля после срабатывания предохранителя. Совместив начало систе­мы координат с моментом перехода напряжения u_s\—и_е2 через нуль в положительную область, найдем среднее значение напряжения:

210

f7_d = -~ JKrKrc/_ssinco№/ = -i-K6".100X

90

X (~cos 210° + cos 90°) = 74,3 В, и среднее значение тока:

Задача 2.48. Трехфазный мостовой неуправляемый выпря­митель (рис. 2.89) работает на нагрузку, состоящую из последова­тельно соединенных реактора с индуктивностью La^oo, резистора с сопротивлением #d=0,2 Ом и противо-ЭДС E_d=2\0 В. Действую­щее значение напряжения вентильной обмотки t/_fi=220 В, а реактив­ное сопротивление на фазу Х^ =0,5 Ом. Определить среднее зна­чение выпрямленных напряжения и тока, а также угол комму­тации.

Решение. Предположим, что угол коммутации меньше 60°, тогда искомые значения могут быть определены, как в задаче 2.42.

Результаты расчетов будут: /_ri=380,7 a; £7_d=286,l в; y=77,1°>->60°.

Таким образом, принятое предположение оказалось неправиль­ным и надо учитывать угол задержки включения а*.

Теперь предположим, что выпрямитель работает в диапазоне углов задержки 0°<«*<30° при у=60° (рис. 2.90). в этом диапа­зоне неуправляемый выпрямитель работает так же, как управляе­мый при угле управления а=а*, поэтому справедливы следующие-уравнения:

а т! o^jL- ti ^o[cosa + cos(a-f-Y)]. V_d = U_diucoso.— ЪЩр» ^Ud = 2 *

COS (a "-г- Y) =iCOS a — _f— — •

v V2 U_ssin(n/p)

Принимая во внимание тригонометри4еские соотношения

cos x + cos у = 2 cos ——- "cos о—

en = ^Х + У , ^% — У

cos x — cos у = —\2 sin ~- sin ~—

получаем:

L/_d = ^₀cos(Y/2)l/ i.

sin²(Y/2) $U_sstoL{*/P)

p Id.Xf

йп(_в+г/2) = _в81п(у/2)р^_г-Подставив значения /?==3 и y = 60°, а также

найдем:

^2 -9 , Г о

т/Т Л**т

sin(a + 30°)= |/ "з"— •

Воспользовавшись уравнением для пепи постоянного тока после преобразований получим:

Л 1 / 9 \² /3 \² /3 \²т

/л= - =

Подстановка численных значений дает следующий результат: Г \ I 9 \^а

^{—210-0,2 +j^7} 4" [^rf ²⁰⁰² [°'²² + ³("1~ °"⁵)²~

0,2² + 3 ^-0,6^

— 210²3 f — 0,5] .

Условие /^^0 определяет единственное решение: 1_й = 353,3 А,

следовательно,

U_d = 353,3-0,2 + 210 = 280,7 В

и

Л /""2" 353,3-0,5\ а* = arcsin [у _ш. 1-30° = 16,2° <30^е,

что подтверждает сделанное предположение.

Задача 2.49. Преобразователь со схемой соединений ЗФ2Н6П, показанной на рнс. 2.91, работает в инверторном режиме. Построить кривые напряжений на полюсах инвертора и тока тиристоров. Опре­делить среднее значение активной мощности, поступающей в сеть переменного тока, при условии, что сУ₈=220 В, /=50 Гц, R_d=\ Ом, Ld^oo, £d=400 В, а=120°, а индуктивность трансформатора: а) 1_т = 0, б) I_Y=1 мГн.

Активным сопротивлением трансформатора пренебречь, вентили идеальные.

Решение, а) Тиристоры Т_и Т_г, Т₃ коммутационной группы / коммутируют между собой, также между собой коммутируют ти­ристоры T_at Ть, Т_с коммутационной группы //. Напряжение и& равно разности напряжений двух последовательно соединенных ком­мутационных групп. Последовательность коммутаций в группе / и ее напряжение «di показаны на рис. 2.92, а на рис. 2.926 приведены последовательность коммутаций в группе II а ее напряжение Udu (кривые напряжений «di и «ап показаны жирными линиями).

Поскольку индуктивность L_d сглаживающего реактора весьма велика, то ток ia — постоянный.

84

Среднее значение выпрямленного напряжения

U_а = U_dl -U_A11=2 VTU_S 4- sin cos а -

Jdll

= 2^2 - 220 — sin -4r cos 120° = —257,5 В.

чх о

Кривые токов тиристоров показаны на рис. 2.92,0, г. Уравнение напряжений цепи постоянного тока в соответствии с рис. 2.91:

U_d-\-E_d—/_d'fld=0.

Ш

6}

того, как начинается комму­тация в другой группе. С учетом коммутаций урав­нение напряжений цепи по­стоянного тока становится* следующим:

U_d--^jf+E_d-I_dR_d=Q.

З

wt Рис. 2.93. Диаграммы на-—пряжений и токов инверто­ра на рис. 2.91 при 1*_лфЪ.

и И м

десь падение напряже­ния, обусловленное комму­тацией, удвоено, так как коммутации происходят в обеих коммутационных группах.

Z

■л

x

[та {п (п {та {п

и

-т4

Дг

Г9 L_d Rd Дз

cot

Рис. 2.94. Схема выпрями* ^v теля к задаче 2.50.

Среднее значение тока в цепи постоянного тока будет равно; Ud+Ed -257,5 + 400 2Х_У - 2-0,001.314

2п/р

2гс/3

Угол коммутации может быть определен из уравнения

Id*,

cos (а + v) = ^{cos а} — ,r— ' »

К2 l/,sinrc//?

т. е.

cos (120^е-f _Y) = cos 120^е

109,5-0,314 VT-220 sin -y

откуда y = 6,3*. 86

Напряжения u_di и «dii коммутационных групп I и II пока­заны на рис. 2.93,а, б, а токи тиристоров — на рис. 2.93,е, г. Видно, что интервалы коммутаций обеих коммутационных групп не совпа­дают во времени, т. е. сделанное предположение является пра­вильным.

Мощность, поступающая в сеть переменного тока, равна: Р= | U_dI_d | =257,5 • 109.5=31 800 Вт=31,8 кВт.

Задача 2.50. Трехфазный полууправляемый мостовой выпря­митель питает активную нагрузку через реактор с индуктивностью Ld^oo (рис. 2.94). Определить угол управления, если i7_s=110 В, Rd= 1,285 Ом, P_d= 12,85 кВт. Определить средние и действующие значения токов тиристоров и диодов, а также среднее и действую­щее значения тока вентильной обмотки трансформатора.

Решение. Так как индуктивное сопротивление реактора не­ограниченно большое, то выпрямленный ток будет идеально сгла­жен и среднее значение выходного напряжения выпрямителя можно определить как сумму средних значений напряжений обеих комму­тационных групп моста:

Ud=Udio[l-\-cos а),

где Udio — среднее значение напряжения неуправляемой группы. .При /7=3 находим:

U_dl^VTU_s ^-sin у =128,5 В; среднее значение выпрямленного напряжения дол кно_ быть равно:

U_d = l_dR_d- Ущ- *d = VfWd =V 12,85-10*. 1,285 = 128,5В. Значит,

COS а = 77— — 1=0, ^udio

а=arccos 0=90°.

Ha рис. 2.95 показаны моменты коммутации вентилей в обеих группах. Мгновенные значения напряжения u_d показаны вертикаль­ной штриховкой.

Выпрямленный ток

'd= R_d -1,285-^{1Ш А}'

Средние значения токов ^вентилей

/т.ср = 'д.ср = -з^-=33,3 а.

Д

= 57,8 А.

ействующие значения токов вентилей

1_Т /д

Уз

Действующее значение тока вентильной обмотки трансформа-

тора

*d сс

~u~_s2 "S3 "si "sZ "s3 "S1 "sZ "S3 "SI

Рис. 2.95. Диаграммы напряжений и токов в схеме на рис. 2.94.

Задача 2.51. Для схемы выпрямителя, показанной на рис. 2.96, определить среднее значение выпрямленного напряжения I! состав гармоник выпрямленного напряжения, если дано, что про­водимость непрерывная.

Р е ш е и и е. Два последовательно соединенных трехфазных мо­ста разделяются на четыре отдельные коммутационные группы. Коммутация каждой группы не зависит от остальных трех. Поэтому среднее значение выпрямленного напряжения равно сумме средних значений выпрямленных напряжений двух мостов, т. е.

1/^0=2-2,34 с/,,,

Суммировать можно и мгновенные значения. Так как выходные напряжения двух шестипульсных мостов смещены по фазе на 30°, то представленная на рис. 2.96 схем? будет двенадцатипульсной, следовательно, выпрямленное напряжение будет содержать следую­щие гармоники:

п=ср=\2, 24, 36 ...

Задача 2.52. Определить среднее значение выпрямленного напряжения для выпрямителя со схемой соединений, показанной на рис. 2.97, при условии, что прово­димость вентилей непрерывная. Трансформатор и диоды идеаль­ные.

Решение. Схема соеди­нений может быть разложена иа две незазиснмые коммутационные группы, диоды каждой группы коммутируют между собой неза­висимо от диодов другой группы.

В группе / тот диод проводит ток, анод которого имеет наи­большее положительное напряже­ние. Поскольку одно из симмет­ричных фазных напряжений все­гда больше нуля, диоды Д_а, Дь и Д_с никогда не проводят ток.

В группе // тот диод проводит ток, катод которого имеет наи­большее отрицательное напряжение. По причинам, указанным выше, диоды Да, Д_е н Д/ никогда не проводят ток.

Вследствие этого схема соединений становится простой схемой выпрямителя ЗФ2Н6П, в которой

Vdio = 2 V2~U_S ~sin ~=2,34U_S.

2.4. ЗАДАЧИ ПО ПРЕОБРАЗОВАТЕЛЬНЫМ ТРАНСФОРМАТОРАМ

З

Рис. 2.97. Схема выпрямителя к задаче 2.52.

адача 2.53. Идеальный выпрямитель со схемой соедине­ний 1Ф1НП7, работающий на активную нагрузку, присоединен к сети через однофазный трансформатор с идеальной магнитной си­стемой (рис. 2.98). Поток рассеяния трансформатора пренебрежимо мал. Построить кривые токов в обмотках трансформатора и найти средние и действующие значения токов при условии, что активное сопротивление цепи сетевой обмотки, отнесенное к вентильной об­мотке, равно Яр, а активное сопротивление цепи вентильной об­мотки вместе с нагрузкой равно R_s.

Решение. По условию поток рассеяния трансформатора ра­вен нулю, поэтому трансформатор может быть заменен реактивным сопротивлением, через которое протекает ток намагничивания /"_и (рис. 2.99). Благодаря наличию диода ток вентильной обмотки i_tt как показано на рис. 2.100,а, является пульсирующим током одного знака. Ои может быть разложен на постоянную составляющую /_в и переменную составляющую /₅₀ (рис 2.100,6, в). Предположим в первом приближении, что токи в двух других ветвях эквивалент-

_{А Л}

X

г

9ер

х т а)

id

at

ait

Рис. 2.100. Диаграммы токов на стороне вен­тильной обмотки транс­форматора (к зада­че 2.53).

Ю

ной схемы будут иметь ту же самую форму, т. е.

•fp — ' pep 4~ ¹

pa

Поскольку i_p=i-\-i_s, то для составляющих токов будут спра-

ведливы следующие уравнения:

|ДСР

scp>

4» +

Предполагая, что сердечник трансформатора имеет неограни­ченно большую магнитную проницаемость и может иметь неограни­ченно большую магнитную индукцию (рис. 2.101), получаем <ц» = 0, а токи сетевой и вентильной обмоток равными:

i_D = h> I

pep

Однако такой идеальный трансформатор очень сильно отли­чается от любого реального трансформатора. Это видно из рас­смотрения уравнений напряжений

u_p=ipRp-\-u_B.

Напряжение и₈ возникает при изменении во времени потоко­сцепления обмотки:

№

dt

Ток сетевой обмотки содержит постоянную составляющую. В цепи нет источника постоянного напряжения, поэтому постоянная составляющая тока может быть скомпенсирована только за счет постоянной составляющей индуцированного напряжения dW/dt. Из этого следует, что уравнения напряжений можно разделить на

>-

в Щ	W
	н
0	F
	т
-Bs

Рис. 2.101. Характеристика на­магничивания идеального не-иасыщающегося стального сер­дечника трансформатора (к за­даче 2.53).

Рис 2.102. Характеристика на­магничивания идеального насы­щающегося стального сердеч­ника трансформатора (к за­даче 2.53).

уравнения для постоянных и переменных составляющих:

d

т

W,

0 = 1 рсгДр ф

dV_a

где *¥i обозначает ту часть потокосцепления обмотки трансформа­тора, которая изменяется линейно во времени (т. е. индуцирует постоянное напряжение), а Ч?_а обозначает ту часть потокосцепле­ния, которая вызывает появление переменного напряжения. Так как первая составляющая потокосцепления изменяется с постоянной скоростью, то

dt

-= -/_/Юр/?_/, = const.

В действительности сердечник трансформатора имеет ограни­ченную насыщением стали магнитную индукцию. Пользуясь идеаль­ной кривой намагничивания с учетом насыщения (рис 2.102), кото­рая ближе соответствует действительной кривой намагничивания, нетрудно видеть, что описанная выше работа трансформатора с на­грузкой, состоящей из однонаправленного выпрямителя, невозмож­на. Насыщение сердечника не позволяет потокосцеплению выходить за пределы W_s или —W_s. Следовательно, при насыщении трансфор­матора должно выполняться⁴ следующее условие:

/р cpRp—0.

Поскольку по условию задачи сопротивлением R_P нельзя пре­небречь, то только /_{р С}р может быть равно нулю, т. е. через сете­вую обмотку трансформатора будет протекать только переменный ток. Таким образом, уравнения для токов при насыщении транс­форматора примут вид:

l_Pj — V° W

Отсюда видно, что апериодическая составляющая тока намаг­ничивания трансформатора с насыщающимся сердечником и нагруз­кой, состоящей из однонаправленного выпрямителя, будет равна среднему значению тока выпрямителя, т. е. появится МДС, приво­дящая к одностороннему намагничиванию сердечника трансформа­тора. На рис. 2.-103 показаны кривые, характеризующие процесс намагничивания. Сначала тока насыщения нет, среднее значение потокосцепления уменьшается линейно и i_p=is, а /^^=0, при этом положительные и отрицательные производные потокосцепления не равны, поскольку положительные напряжения u_s отличаются от отрицательных на падение напряжения i_pR_p.

Когда яотокосцепление достигнет значения —W_ai ^дальнейшее его изменение прекратится, т. е. d^xt?/dt=0 и, следовательно, u_s=0, ток сетевой обмотки - будет ограничиваться только активным со- _{и и} противлением R_p. Имен-

но эти отрицательные импульсы тока иамагни- ait чивают трансформатор. Форма кривой и дейст- вующее значение тока сетевой обмотки отлича- ^^Y7r ^-v У ются от формы кривой я

( \ ^{s p}-J~—\ f /~*\ f~\ ^ujt действующего значения ilp j ' ' *" гока вентильной обмот-

Ш£ кн. Вычислим угол 6, в течение которого сердеч­ник трансформатора на­ходится в насыщенном состоянии, н дополняю­щий его до 2л угол \.

Рис. 2.103. Диаграммы работы однофазного трансформатора с иде­альным насыщающимся сердечником, работающе­го в однонаправленной однопульсной схеме (к задаче 2.53).

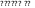
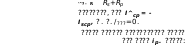
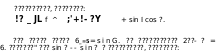
Поскольку

ад

2(^ + Я_р) -после некоторых преобразований найдем:

г

Видно, что действующее значение тока сетевой обмотки в ре­зультате одностороннего намагничивания увеличивается. Например, если Rs—50Rp, то /_p=»3/_s. Ситуация в реальном трансформаторе лучше, так как в нем магнитный поток продолжает изменяться

Рис. 2.105. Диаграммы работы выпрямителя на рис. 2.104.

и -лг изгибом петли гистерезиса. Это означает, что к трансформа­тору продолжает прикладываться напряжение и тем самым огра­ничивается рост намагничивания.

Вследствие одностороннего намагничивания трансформатора схема 1Ф1Н1П применяется только в слаботочной технике.

Задача 2.54. Определить ток сетевой и вентильной обмоток и мощность трансформатора (отдельно для броневого и стержне­вого), питающего выпрямитель со схемой соединений 1Ф1Н2П На­грузка на выпрямитель состоит из резистора с сопротивлением Rd и реактора с индуктивностью Ld^zft- В броневом трансформаторе сетевая и вентильные обмотки расположены на одном и том же стержне магнитопровода (рис. 2.104). Кривая тока вентильных об­моток имеет форму прямоугольного импульса (рис. 2.105,6, в). Ре­

зультирующая МДС в среднем стержне будет: F₀ = ipWp + i_SiWs—h*at>s*

т. е.

Поскольку ток tea—t«i переменный, условие 1_Р ср = 0 удовлет­воряется только для случая, когда F₀=0 (см. задачу 2.53). Соот­ветственно кривая тока i_p имеет форму, как показано на рис. 2.105,а_

Расчетная мощность трансформатора определяется следующим; образом:

/ -/

Ss = и_л1_я + c/,₂/_S2=K2 Up!_d;

s_P=u_pi_p-.

•им;

и

то находим:

-u_s

™S 2V~2

U_dI_d=P_d,

В стержневом трансформаторе обмотки располагаются на двух отдельных стержнях магнитопровода (рис. 2.106). Кривые токов вентильной обмотки (рис. 2.107Д в) такие же, как и в случае «а».. Для того чтобы иайти ток сетевой обмотки, запишем выражения; для МДС в стержнях (МДС в ярмах можно пренебречь):

Эта система уравнений решается следующим образом:

„ hi + *мш ^ld

F₀ = ™s 2 ^=Ws ~2~

Построив на основе этого уравнения зависимость тока сетевой обмотки от времени (рис. 2.107,г), можно получить также МДС одностороннего намагничивания путем последовательных вычисле­ний МДС в стержнях магиитопровода от одного полупериода к дру­гому.

ls1 ш

hz

Ш 6)

ш

cut

tut

6)

г)

wt

.

в)

5 z

Рис. 2.107. Характеристика диаграммы работы выпрями­теля на рис. 2.106.

Расчетная мощность трансформатора вычисляется следующим образом:

Id

I si ~ Is2 — 2 ' I р ⁼ 'd

s

щ

u_s1 = и_ш =

■ = и

Р

'р

w

U

Р2

pi — V-nv —

*р .

S_s = 2U_slI_sl=V2-^f-U_pI_d-_t

Sp = 2U_plI_u=—UpI_d.

Поскольку

имеем:

W_p Я

и, подставив P_d — U_dI_d, получим:

\ + V.2 „

Таким образом, находим, что расчетные мощности броневого и стержневого трансформаторов одинаковы. Однако стержневой трансформатор не может применяться из-за значительного односто­роннего намагничивания.

Задача 2.55. Как показано в задаче 2.54, недостатком стерж­невого трансформатора является значительное одностороннее на­магничивание. Доказать, что одностороннее намагничивание исчез­нет, если соединить вентильные обмотки по схеме «зигзаг» (рис. 2.108).

Решение. Для доказательства запишем уравнения МДС для стержня / магнитопровода

и для стержня 2 магнитопровода

Fff=ipWp-\-iH2W_s—isiWs.

7—Q

Решив эти уравнения, получим Fo=0, а для тока сетевой об­мотки — только переменную составляющую:

. _ Ws_

lP~ w_p ™ ^tsz)'

В данном случае расчетная мощность трансформатора 5= =l,34Pd, т. е. такая же, как и в задаче 2.54.

Из задач 2.54 и 2.55 следует, что для исключения нежелатель­ного одностороннего намагничивания магнитопровода трансформа­тора, питающего выпрямитель с однонаправленной схемой, токи вентильных обмоток, расположенных на каждом стержне магнито­провода, должны создавать переменную МДС.

Задача 2-56. Выпрямитель со схемой соединений ЗФ1НЗП присоединен к сети через идеальный трансформатор, обмотки кото­рого соединены по схеме «звезда — звезда». Выпрямитель нагружен на последовательно соединенные активное сопротивление R_d и ин­дуктивность £d~°° (рис. 2.109). Построить кривые токов сетевых и вентильных обмоток и вычислить расчетную мощность трансфор­матора с выведенной нейтралью и с изолированной.

• Решение. Сначала определим МДС в стержнях магнитопро­вода, пренебрегая МДС в ярмах и МДС холостого хода. Результи­рующие МДС в стержнях магнитопровода равны МДС односторон­него намагничивания F₀ и одинаковы для всех стержней:

* ^US1 ^usz % %

(ц j £ zx зж

I

<-Sl

d

Id

i

Ls3

1

d

_P

id

wt

F₀=w_si_s\ —Wpip i; Fq=w_sis2—®> p tp 2', Fq= Wsi_sz—Wpips. Уравнение токов

ipi~\'ip 8~r*t p з=*о»

где to — ток нейтрали.

Эти четыре уравнения содержат пять неизвестных. Пятое уравнение может быть составлено на основании следующих рассуждений.

Ток через нулевой провод может протекать только в том случае, если токи сетевых обмоток содержат гар­моники с номерами, кратными трем. Так как сеть дает напряжение про­мышленной частоты и предполагает­ся, что трансформатор — линейный элемент, то любая гармоника в токах сетевых обмоток появляется в резуль­тате работы вентилей, присоединен­ных к вентильным обмоткам транс­форматора. Гармоники токов вен-

Рис. 2.110. Диаграммы работы вы­прямительного трансформатора на рис. 2,|09_?

тилышх обмоток имеют номера!

n=cp-\-l(с=Ю, 1, 2...; р=3),

откуда пФЪк (k=\, 2 ...), и, таким образом, через нулевой провод не будут протекать токи высших гармоник. Следовательно, пятым уравнением будет i'o=0. Это уравнение означает также, что наличие нулевого провода не влияет на работу трансформатора. Система уравнений решается следующим образом:

1

'/32 —

^ 3 '« *~ 3 3 *^5SJ Юр •

/

W_n

1 _2_ J_ \

з «si +з *s₂ — з hzJ

Рш = ttl_S

с51 — з »** Hh з

^Sl *T" "T"

3 *

Соответствующие кривые показаны на рис. 2.110. Расчетная мощность трансформатора вычисляется следующим образом:

/_/_/_/_. *4 ■

ms1 *S2 * ss "' 's

уж '

2п U_d

U

1,17 '

3/6

_sl=U_s2 = U_s,=:U_s = U_d кУ2

P_d=l,48P_d;

, f 1 w^z_s / 4 _л 9n 1 2*z \

i»e yj

Id',

2rc

u

P_d = l,21P_d;

_pi = v_p2 = v_pa = u_p = -_w

2

5_p-3c/_p/_p-₃^-

5=­

s_p + s_s

= l,34P_rf.

Задача 2.57. Построить кривые тока сетевой обмотки для схемы соединений, показанной на рис. 2.109, если нагрузка выпря­мителя чисто активная, т. е. Ld=0. Определить влияние вывода нейтрали на стороне сети и сопоставить результаты с результатами, полученными в задаче 2.56.

7* 99

Решение. Для трансформатора с Изолированной нейтралью пригодно решение, полученное в задаче 2.56:

lP* ⁼ ( 3 '« ~ 3 *** ~~ 3 ^ls3J w j '

г. *SI Н" 'S2 + *S3 *d

r„ — w_s з =- од -g-*

Основная составляющая с частотой 150 Гц в односторонней МДС возникает от гармоник тока вентильных обмоток с номерами, кратными трем. Если нейтраль выведена, то через сетевые обмотки будут протекать токи нулевой последовательности, действуя как размагничивающие; цепь, через которую проходят эти токи, замкну-

ч		il i
i	* 1* |« lx f*
	a	Ю Г) **
£s3		6)

Рис. 2.Ml. Характерные диа­граммы работы выпрямителя со схемой ЗФ1Н1П, работаю­щего на активную нагрузку, при соединении обмоток транс­форматора по схеме «звезда — звезда» (к задаче 2.57).

та через выведенную нейтраль. В результате этого МДС перемен­ного тока нулевой последовательности равна нулю и одностороннее намагничивание соответствует только току /d/З. Кривые токов сете­вых обмоток МДС для обоих случаев показаны на рис. 2.111.

Основная роль нулевого провода состоит, таким образом, в том, что он предупреждает развитие одностороннего намагничивания на частотах высших гармоник.

Задача 2.58. Выпрямитель со схемой соединений ЗФШЗП работает на нагрузку, состоящую из последовательно соединенных резистора с сопротивлением Rd и реактора с индуктивностью Ld^oo. Схема соединения обмоток преобразовательного трансформатора «треугольник — звезда». Построить кривую тока сетевой обмотки и найти расчетную мощность трансформатора.

Решение. Для трансформатора, соединенного, как показано на рис. 2.112, могут быть записаны три уравнения МДС и три урав­нения токов:

Fff=isiW₈—ip\W_p; Fo=i_s2w_s~ip2Wp; F^iszWs—ipsWp,

и

*ф| =*j»l—lpb\ 1ф2 = 1р2—ip It

i(t>3⁼ips—ip2-

Этр система из шести уравнений с'семью неизвестными (токи сетевых обмоток, токи в сети и МДС F). В трансформаторе, обмот­ки которого соединены в звезду, сумма токов сетевых обмоток равна нулю, что может быть попользовано в качестве дополнитель­ного уравнения. В данном случае через обмотки, соединенные в «треугольник», могут протекать токи нулевой последовательности, которые нам пока неизвестны. Можно сказать лишь, что из-за на­личия активных сопротивлений сетевых обмоток средние значения их токов равны нулю.

Недостающее уравнение может быть записано для односторон­ней МДС F_0l которая может быть постоянной или переменной. Од­нако при соединении обмоток в треугольник может появиться МДС, противоположная по знаку переменной МДС. Магнитный поток ну­левой последовательности замыкается вдоль путей рассеяния, соот­ветственно степень компенсации односторонней МДС зависит от кон­струкции трансформатора. Далее будем считать, что компенсация односторонней МДС полная (т. е. односторонняя МДС не содержит переменной составляющей).

Используя это допущение, записываем интеграл

4" ^ F_udv>t = j (i_8fW₈ — i_piw_p) dbt. о о

МДС'в первом стержне магнитопровода F_Q = i_Siw_s — i_piw_p.

Имея в виду, что

2тс

I_d при 0 <: cot <; -у;

2rc

О при -3- < cof < 2я

2я

dtot = 0,

находим значение односторонней МДС:

F(f=w_sI_d/3.

Теперь Можно Достаточно просто вычислить токи сетевых обмоток:

Л td\ Щ / & ± J_ \ щ .

»Р1 = ^« ф)~щ_р~^ая;\ 3 3 *^s2~ 3 ^lss) w_p ¹

Л ^ld\™L-_l L • . ² i JLi \ ^w*

»P2=1'S8 — ~Z } W_p'~\ 3 ™ + 3 ^h2 3 ^ls3j »

Л J£t_f JL/ ¹ I . ² i ^ ^ш*

«ре—^'s3— з j _Шр ^— з hi— з з »S3J щ •

Эти уравнения такие же, как и для схемы соединения обмоток (задача 2.56), следовательно, и расчетная мощность трансформатора будет такой же. Односторонняя МДС, пропорциональная одной тре­ти тока нагрузки, возникает и в данном случае.

Токи в сети

w_s . .

Щ — _w Vpi —

'Ф² W_p ™

'ф8— _ш (*/;з— 'pi)-Р

Кривые этих токов показаны на рис. 2.113. Как и в задаче 2.56,

В соответствии с рис. 2.113

7Ф⁼ W_p V ~ ^Id'

т. е. / ф = УТ/_р.

Задача 2.59. Выпрямитель со схемой соединений ЗФ1НЗП работает на нагрузку, состоящую из последовательно соединенных активного сопротивления Rd и индуктивности Ld^°° (рис. 2.114). Построить кривые токов сетевых обмоток и найти расчетную мощ­ность преобразовательного трансформатора со схемами соединения обмоток а)—«звезда—зигзаг» и б)—«треугольник — зигзаг».

Решение. В предыдущих задачах было показано, что расчет­ная мощность не зависит от коэффициента трансформации. Поэтому для упрощения примем, что w_p/w_s—\.

а) При w_£—w_p=w уравнения для схемы, показанной на рис. 2.114, будут:

Fo=w(i_sl~i_eS—ipi); F(f=w (t_fi3—/.a—i _Ps);

Решив первые три уравнения, получим:

следовательно, токи сетевых обмоток будут:

*pi='si—1вз:

1р2⁼⁼1в2—Ktli

На рис. 2.115 показаны кривые, построенные на основании этих уравнений. При вычислении расчетной мощности трансформатора на­пряжения вентильных полуобмоток суммируем геометрически (рис. 2.116) и получим:

2 .

3 '<*>

Jk-_ Ча . _и-_v, Ча

УЪ~\,ПУЪ' ^{р s} 1,17^3'

2 _ V2

S_s = 6I_SU'_S = j |7 Pd\ S_p = ofpUp — j |7

s = -

Щ-g "T" S_p

24-

2-1,17

l,46P_rf.

б) В задаче 2.58, рассматривая трансформатор с обмотками, со­единенными в треугольник, мы выяснили, что постоянная состав-

л

6х

isf г к

а) fx

_{□ □ □}

5)

п ^г'п п

П П Q.

П "\П . p

lo

Ы

X)

яющая односторонней МДС мо-cot жет быть вычислена как среднее значение МДС вентильных обмо­ток, расположенных на одном и том же стержне магнитопровода. Такой результат получен на осно-wt вании предположения, с одной сто-—*~ ропы, что средние значения токов сетевых обмоток всегда равны ^wt нулю, а следовательно, и средние значения МДС сетевых обмоток равны нулю, а с другой, что пере-—мешая составляющая односторон­ней МДС равна нулю (предпола-^и* галось, что компенсация перемен­ной односторонней МДС полная). _Ш1 С учетом этого, а также того, что —— греднее значение разности токов {«] и 7_s3 равно нулю для вентиль­ных обмоток трансформатора, по­казанного на рис. 2.114, получаем:

Рис. 2.115. Диаграммы работы выпрямителя (к задаче 2.59).

2я

Отсюда видно, что уравнения токов сетевых обмоток идентичны уравнениям, полученным для схемы «звезда — зигзаг». Токи сетевых

обмоток (рис. 2.117):

i$i—ipi—i v з—U i~He2"—2i_S3» 1ф2⁼⁼'р2—ipi = *в2~Н«з—2i_fii; *фз⁼*рз—ip2—is\ -М"*з—2i«2.

Кривая тока Ц\ показана на рис. 2Л\5,ж. Поскольку через обмотки, соединенные по схеме «звезда — зигзаг», проходят одина­ковые токи, расчетные мощности трансформаторов также одинаковы

й равны:

5=l,46P_d. Действующие значения токсяз в сети

'ф

_-/4

4/²_d

В этом случае /ф = "^/"3/_р, поскольку I_p—I_d У2/3.

Задача 2.60. Выпрямитель со схемой соединений ЗФ1Н6П работает на нагрузку, содержащую резистор с сопротивлением Rd и реактор с индуктивностью Ld^°°. Построить кривые токов сете­вых обмоток, определить одностороннюю МДС и расчетную мощ­ность трансформатора. Схема соединения обмоток трансформатора: а) «звезда — звезда», б) «треугольник — звезда».

Рис. 2.118. Схема вы­прямителя к задаче 2.60.

<Ц1
гЦ А	К
			Iks

slypt

S6 A S2

_ж

sS;p3 j s3;pZ

Решение, а) При w_p=w_s=w уравнения для трансформатора с обмотками, соединенными по схеме «звезда — звезда» (рис. 2.118), принимают вид:

F(f=w (Ui—isr—i_P i); F_Q=w (/«з—'se—ipi); F(F=w {i₈₅—is2—ipb);

/p1+'p2+'P3=0.

Э

2 , , Д _ .J,, 'pi = ~з~ 'si + 3 *« + 3 ^s

та система уравнений имеет решение:

J_

3

о fee "f" Q Свв •

lp%~ —— h\ + T + T^is*⁺ -

1 ² 1 12 1

*/» — T be + T '«*T ^{/sa +} 3 '*« +3 ^{£sb +} 3 '^se;

На рис. 2.119 показаны кривые токов вентильных обмоток и по­строенные по иим кривые для i_pl и F₀.

б) Если сетевые обмотки соединены в треугольник (см. рис. 2.117), то уравнение

'Чч-Мрг-Ц'рз^О,

как и в части «б» задачи 2.59, должно быть заменено уравнением

поскольку среднее значение разности токов U\—ы равно нулю. Те­перь легко можно вычислить токи сетевых обмоток:

	isx	(в4»
	is*
<Р» =	ы

— 'si -f- tsa ~f" 's4 — he"' Щ — is% + 'ее + 'se-

На рис. 2.120 представлены токи сетевой обмотки и в сети, получен­ные из этих уравнений. Ниже при­веден метод вычисления расчетной мощности трансформатора. Подроб­ные вычисления предлагается сделать читателям. Следует иметь в виду, что поскольку через обмотки, соеди­ненные в треугольник, протекают пе­ременные токи in/левой последова­тельности, отношение междуфазных

токов к фазным равно

Рис. 2.119. Диаграммы работы вы­прямителя по схеме на рис. 2.118.

Параметры

Is

Us

s_s

h /ф

Vp

s_t

С

Id

хема соединений: «звезда — звезда» «треугольник — звезда»

I

УЖ

Ud 1,35

d

уж

U d 1,35

У

Pd

±

1,35

У

Id

2

3

У*

3

u_d

1

Pd

,35 У2

1,35 U4ZP_d

Задача 2.61. Выпрямитель с трехфазной мостовой схемой со­единений работает через сглаживающий реактор с индуктивностью L_d=oo на активную нагрузку. Найти токи сетевых обмоток, одно­стороннюю МДС и расчетную мощность трансформатора, схема соединений обмоток ко­торого: а) «звезда — звезда» и б) «треугольник — звезда».

t

5w

Jx

ut

Ex

Ф1\

Id

TJ"

cvt

rH>h

_—w-

■W-i

-t»—

_—w­

чх—

Рис. 2.120. Диаграммы рабо­ты выпрямителя со схемой ЗФ1Н6П при схеме соединений обмоток трансформатора «тре­угольник — звезда» (к зада­че 2.60).

Рис. 2.121. Трехфазный мосто­вой выпрямитель с обмотками трансформатора, соединенными по схеме «звезда — звезда» (к задаче 2.61).

h		wt
f Хф 2ЛГ &l 1 1 1 1			wt
'Рз	1 I 1 1 '		wt
. L f	_J I I		wt
6	Чу к " eg

Рис. 2.122. Диаграммы работы мостового выпрямителя (к за­даче 2.61).

Решение. Поскольку токи вентильных обмоток переменные, токи сетевых обмоток будут иметь средние значения, равные нулю без какой-либо компенсации одно­сторонней МДС, а кривые фазных токов сетевых обмоток идентичны кривым токов вентильных обмо­ток. Это подтверждается решени­ем соответствующих уравнений.

а) При Wp—w_K—w для схемы да рис. 2.121 получим следующие уравнения:

F₀=w{Ui—ipi)\ Fa=w(i₈2—ip₂)] F(s=w(i_sS—i_ps);

3

2 hi = hi + ^lm + ^lm = °-

Решая эти уравнения, получаем:

3F_n = w I

-2 ^

= 0,

так как

2 '«-л* i=i

Следовательно, F₀=0, и

i_Pi=isu

Ip2—is2,

ips^iss-

б) В трансформаторе, обмотки которого соединены по схеме «треугольник — звезда», фазные токи такие же, как в случае «а», а токи в сети в соответствии с рис 2.117 равны:

*Ф1—ipi—*p3t

1ф₂ = 1р₂—ip\\ Ц>3 = *рЗ^Р2.

На рис. 2.122 показаны соответствующие кривые. Порядок вы­числения расчетной мощности трансформатора приведен ниже, по­дробные вычисления предлагается выполнить читателям.

Параметры

Схема соединений: «звезда — звезда» «треугольник — звезда»

и,

2,34

2,34 ^^с

и.

2,34

У 6

2,34 * '

S l,05P_d

Полученные результаты свидетельствуют о том, что при этих двух схемах соединений расчетные мощности трансформаторов не­значительно превышают мощность нагрузки.

Задача 2.62. Выпрямитель со схемой соединений ЗФ2Н6П работает через сглаживающий ре­актор с Ld^oo на активную на­грузку (рис. 2.123). Построить кривые токов сетевых обмоток, если магнитная система трансфор­матора линейна, а коэффициент искажения формы кривой напря­жения источника питания равен нулю.

Решение. Токи сетевых об моток определяются напряжением источника питания, группой соеди­нения обмоток трансформатора, формой кривой намагничивания и токами вентильных обмоток. От­носительно последних можно ска­зать следующее.

Влияние источника питания ш приводит к появлению токов ну левой последовательности в вен тильных обмотках, соединенных в

Треугольник, поскольку по уело- Рис. 2.123. Трехфазный мосто- рию напряжение источника пита- вой выпрямитель со схемой со- ния представляет собой папряже- единений обмоток трансфор- ние основной частоты и не содер- матора «звезда — треугольник» жит высших гармоник, а кривая (задача 2.62).

намагничивания трансформатора линейная. В установившемся ре­жиме через обмотку, соединенную в треугольник, не может протекать постоянный ток, так как в цепи отсутствует гене­ратор постоянного тока, который бы его ■поддерживал, а пе­реходная составляющая постоянного тока, если она возни­кает, затухает благодаря активным сопротивлениям обмоток, кото­рые не равны нулю. Из изложенного выше следует, что токи вен­тильных обмоток определяются исключительно работой вентилей.

Рис. 2.125. Диаграммы ра­боты выпрямителя по схеме на рис. 2.123.

Поскольку в токах 1ф_Ь *ф₂ и 'фз могут содержаться только гармоники с номерами n=ztcp+\ (с=0, 1, 2, ...; р=6), гармоники тока с номерами, кратными трем, не могут появиться ни в этих токах, ни в токах вентильных обмоток. Следовательно, выпрямитель также не генерирует токи нулевой последовательности. В токах сетевых обмоток тоже не могут содержаться составляющие тока нулевой последовательности, поскольку нейтраль не выведена.

Отсюда видно, что и токи сетевых обмоток, и токи вентильных обмоток имеют только составляющие прямой и обратной последо­вательностей. Следовательно, может появиться компенсирующая МДС к каждой составляющей МДС и не может появиться односто­ронняя МДС нулевой последовательности:

F₀=0

и

ИО

Ёоспользовавшись уравнениями

'ф!—l"ei-j is2l

*ф2 ⁼ '«2—'«3»

получим (рис. 2.124):

'ря — 'ее — з 'фа "т~ з 'ф1-Результаты показаны на рис. 2.125.