2 Рис. 2.20. К расчету колебаний выходного напряжения в схе­ме на рис. 2.J9. 50 п - 2 RdCd to '

П

180

1

одставив численные значения, найдем:

2et —

1

"2

2 100-0,001

41

2*50

Обратное напряжение диода определяется как разность мгно­венных значений напряжений ti_ci и u_s. Если разорвать цепь нагрузки, то конденсатор зарядится до максимального значения напряжения u_s. Следовательно, максимальное обратное напряжение на диоде в этом случае будет равно:

^обр.макс = 2 VTV_S ^ 2 VY-110 = 312 В.

Задача 2.3. Выпрямитель со схемой соединения 1Ф2Н2П (см. рис. 2.3), питаемый от сети через трансформатор, работает на активную нагрузку. Определить необходимую емкость фильтра Cd, среднее, действующее и максимальное периодическое значения токов через каждый диод, -наибольшее значение тока в переходном процессе при подключении схемы к сети и напряжение XX вентиль­ной обмотки трансформатора при условии, что £/_с-=50 В; /d—10 А; f=60 Гц.

Примем, что среднее значение падения прямого напряжения на диодах равно AU_n=\ В, а пульсации напряжения на выводах нагрузки должны быть не более 2% (определяются как отношение действующего значения переменной составляющей к среднему зна­чению выпрямленного напряжения Ud)-

Решение. Задача решается при помощи графиков, приве­денных во вводной части. Обозначим через R сопротивление заме­щения трансформатора. Считая, что напряжение КЗ соответствует обычным значениям для трансформаторов рассматриваемой мощ­ности, примем отношение R/Rd равным 10%.

По данным нагрузки находим #d=£Af//d—50/10=5 Ом.

Согласно рис. 2.10 заданное условие по пульсациям удовлетво­ряется при значении (nRdCd=S0. Соответственно

3

30

0

2

С_л = ;

^/=1Т4^=⁰'^0191Ф=^{19 100 мкФ}' Из рис. 2.9 находим:

V2U~ ^Us

-=0,76

и, следовательно,

U_{B макс}=50/0,76=66 В.

Максимальное напряжение XX вентильной обмотки трансфор­матора найдем, прибавив к этому значению падения напряжения на двух последовательно соединенных диодах:

U*_smKC = U_S№KC -f 2Д*/_Д = 66 + 2 = 68 В.

ч
ч	/%	/ \
1	r \	/ Л
	V Л
ft	\ \	//\
//	\ \	// \ cut
		""»
	яд ,	Шк зк
		~ud=us

_{Рис. 2.21. Диаграммы токов и Рис. 2.22. Диаграммы токов}

напряжений управляемого выпря- и напряжений неуправляем

мителя со схемой 1Ф1Н1П, рабо-. мого выпрямителя со схемой тающего иа чисто индуктивную 1Ф1Н1П, работающего на

нагрузку (к задаче 2.4). чисто индуктивную нагруз-

ку (к задаче 2.4).

Следовательно, действующее значение напряжения XX вентиль­ной обмотки трансформатора должно быть равно:

U*_s — U*s№i<c/V2~ = 48>² В. Среднее значение тока в каждом диоде

/д.ср=/_й/2=10/2х=5 А.

Из рис. 2.11 находим действующее значение тока в каждом диоде:

/д=/д.ср2,3=5.2,3=11,5 А.

Из рис. 2.12 определяем максимальное периодическое значение тока в каждом диоде:

/д.макс=/д-ср-6,3=5-6,3=31,5 А.

В соответствии со сделанным допущением эквивалентное актив­ное сопротивление трансформатора равно:

R=O,lR_d=0,l-5=0J5 Ом_

Следовательно, наибольшее Значение тока' й переходном tipd цессе включения составляет:

/д.нб=*7*₈ ма.<с//?=68/0,5=136 А.

Задача 2.4. Однофазный однонаправленный однопульсный управляемый выпрямитель работает на индуктивную нагрузку Ld= =20 мГ«. Преобразовательный трансформатор идеален, напряжение вентильной обмотки трансформатора t/_s=100 Б. Определить средние значения токов нагрузки для углов управления «=0° и а=60°.

Решение. Так как нагрузка чисто индуктивная, то все на­пряжение преобразователя приложено к индуктивности. В устано­вившемся .режиме положительные и отрицательные площади под кривыми напряжения на индуктивности будут равны. Из рис. 2.21 следует, что угол выключения вентиля равен а„ыкл=360°—а. Кроме того, напряжение, появляющееся на выходных выводах выпрями­теля, оказывается переменным.

При угле управления а=0 угол выключения а_Выкл=360°, т. е. преобразователь работает в предельном режиме непрерывной про- водимости и все напряжение вентильной обмотки приложено к вы- водам. Дифференциальное уравнение схемы может быть записано в виде —-

-_г— did

Ud = V 2 U_s sin at = L_d ~jf~>

Начальным условием является i_d = 0 при t = 0. Решение уравнения:

VTv_s

Формы кривых тока и напряжения на выводах выпрямителя показаны на рис. 2.22.

Среднее значение тока равно:

V2V* „ ^..,_П[/,

б

fT-ioo

П

nd

ри угле управления а=60° угол выключения а_выкл=360—60= =300°, т. е. проводимость будет прерывистой. Из рис 2.21 следует, что напряжение на выводах равно:

i

если а_выкл + г&ъ < u>t < a± (n + 1) 2ffc,

VY U_s sin cor, если a ± л2гс < u>t < а_ВЬ1КЛ -f л2л;

m

где ft — целое число.

Для периода проводимости может быть записано следующее дифференциальное уравнение:

u_d = VTU_S sin id = l_d —fi­

гфи начальном условии id=b в момент t=afa. Sto уравнение Имеет решение:

id =

[cos а — cos tot]

Форма кривой тока показана на рис. 2.21. Среднее значение тока равно:

^ выкл

а

V¥u_s

' 2nvsL_d [(«вьвсл — ^a) ^cos « + (^sin « — sin ав_ь1КЛ)] =

PTlOO [7 5tt ТС \ Л / Л 5« \ 1

2n- 314-20-10 В результате получаем:

/

I,

_d=13,65 A.

Д. паке

t

Ш Ъх

2Х

Рис. 2.23. Диаграмма тока вы­прямителя, работающего на активную нагрузку (к зада­че 2.5).

Задача 2.5. Падение напряжения в прямом направлении Дс/д в 'кремниевом диоде в зависимости от .протекающего в нем тока £_д задано соотношением

Af/_R=0,85-|40,9-10-³iV

Определить среднее значение потерь в диоде преобразователя со схемой 1Ф1Н1П, работающего иа активную нагрузку. Среднее значение тока нагрузки /д=200 А.

Решение.

т т

Р_д==-1-| J (0,85/_д + 0,9.10-³»²_д)^ ш*

i

1

1_д$ + О,9.10-*-у

о о

/>д=0,85/д._ср+0,9- 10-³/2_д.

Так как /д.ср=/а% то имеем:

/„._cp=/_d=200 А.

Форма кривой тока, протекающего через диод, показана на рис. 2.23.

Соответственно: '

тс

U=-c)t\ /n.MaKcSinco<dcof =

д. махе

*д.маке

/2Д ⁼ ~Lr J 'д-макс sin² <<tf rfco/ = -о

Действующее значение тока через диод

/_д = ~/4 =-=-£■ 200 = 314А,

потери в диоде

Р_д=0,85-200-}-0,9- Ю-³-314²=258,2 В г.

Задача 2.6. Построить кривые токов id, Uu и i_p для схе­мы преобразователя, представленной на рис. 2.24, и сопоставить их с кривой напряжения и_р, сохраняя правильными фазы; вычислить среднее значение тока id. Дано: U_P=100 В, f=-50 Гц, &_тр=1, а= =45°, Rd=*l0 Ом, Ld—0,L^ = 0.Трансформатор и полупроводнико­вые вентили идеальные.

Решение. Кривые напряжения сетевой обмотки и указанных токов показаны на рис. 2.25. Среднее значение тока нагрузки равно:

тс

_{- 4- J -к} ^т* ^slnatd°"=-^Мг^х

а

тс

^{X J sin МЫ = ^2}_w|q°° I — ^cos «flJ/4 = ⁷»^{7 A}-

a

Задача 2.7. Построить кривые токов i_d, Ui, isz и i_p в схеме преобразователя, показанной на рис. 2.24, и сопоставить их с кри­вой напряжения и_р. Определить расчетную мощность трансформа­тора 5_Тр при указанных условиях работы. Дано: t7_p=100 В, f= =50 Гц, коэффициент трансформации 1:1, R&~10 Ом, а=45°, £d~ д-оо t"t ~ 0-Трансформатор и вентили идеальные.

Решение. Требуемые кривые показаны на рис. 2.26. Сред­нее значение выпрямленного напряжения

9 2

U_d = VYU_S — sin ~ cos а = УТ • 100 — cos 45° « 63,7 В.

Среднее значение выпрямленного тока

Vd 63,7 „ /а=^=-щ-=6.37А.

Действующее значение тока в каждой из вентильных полуоб­моток

/ -/ —4*-

«S1 *S2 — 2 *

Мощность вентильной обмотки

5^ = 5_S1 -f 5_S2 = 2U_SyY~=V2~' 100-6,37 = 900 В-A.

_и

tot

Рис. 2.25. Диаграммы напряже­ний и токов в схеме на рис. 2.24, работающей на ак-. тнвную нагрузку без сглажи­вающего реактора (к задаче 2.6).

Действующее значение тока сетевой обмотки

/_p=/_d=6,37 А. Мощность сетевой обмотки

S_p=(7p/p=100-6,37=637 В-А. Расчетная мощность трансформатора

Sp + Ss _637-f-900

= 769 В-А.

Задача 2.8. Построить кривые токов id, in, i_sz и i_v и напря­жения Ud и сопоставить их с кривой напряжения и_р. Определить среднее значение тока нагрузки. Дано: с/_Р=100 В, f=50 Гц, k?_v=l, Rd=W Ом, Ld^oo. Индуктивность трансформатора £_т =10 мГн;

Полупроводниковые вентили идеальные, а=0.

Решение. Кривые напряжений и токов показаны на рис 2.27. Среднее значение выпрямленного напряжения в данном случае равно:

ud = U_dio—^-₁ U_d = I_dR_d.

Решая эти два уравнения совместно, получаем:

Подстановка численных значений дает: /<г=8,22 А.

Задача 2.9. Построить кривые токов i_d, is\, t_s2, lp и напря­жения Ud и сопоставить их с кривой напряжения и_р. Определить среднее значение тока нагрузки. Дано: £/р=100 В, /=50 Гц, А_Тр=1,

Рис. 2.27. Диаграммы напряже­ний и токов (при а=0) в схе­ме на рис. 2.24 с учетом ком­мутации (к задаче 2.8).

/?_d=10 Ом, Ld^oo, Z,~ =10 мГн. Полупроводниковые вентили иде­альные, а=45°.

Решение. Кривые напряжений и токов показаны иа рис. 2.28. Среднее значение напряжения равно:

if—г, 2 1арЬ% . - U_d=VrU_s— cosa

U_d=I_dR_d. Решив эти уравнения, получим:

2 VTU. cos а 2 УТ-100 cos 45^е

= 5,78 А.

Рис. 2.29. Управляемый выпрямитель со схемой 1Ф1Н2П, работаю­щий на нагрузку, представленную противо-ЭДС E_d и резистором Ra.

Задача 2.10. Определить напряжение, показываемое вольт­метром в схеме на рис. 2.29, если U_s=u_si==u_s^=l00 В, £й=70,5 В и а) а=0°, б) а=90°. Ширина импульса управления равна 60°. При­менен вольтметр электродинамической системы. Трансформатор и вентили идеальные.

Решение. Вольтметром измеряют среднее значение напряже­ния иа выходе выпрямителя:

Ud=E_d+IdRd.

а) В соответствии с рис. 2.30 углы включения и выключения вентилей могут быть вычислены из условия равенства противо-ЭДС Ed и напряжения u_s:

Е 70 5 (30° *

«=^arcsinyft7_E ^arcsin VT^m" \ 160-.

что дает а=30° и а_Выкл=*150°, следовательно, вентили не могут включаться при углах, меньших 30°, поэтому при угле управления а=0 необходимы широкие управляющие импульсы. Выпрямленное напряжение равно:

1

Ы/р J * 2гс — sin (30° — 90°)] + 70,5 -

^2-100

1 — о_,1=2 rTz [sin (150° — 90°) —

1

180

50 — 30

= 101 в.

б) При а =90° угол выключения вентилей остается равным «выкл =150° и

Ud = P -ЦТ⁵" [^sin («выкл - у")" sin (а -

+ **. V ~ -*%]Г) ⁼² ~2^— Nn (150- - 90°) -

- sin (90^е - 90^е)] + 70,5 (l -¹⁵°~ ⁹⁰ ) = 85,75 В.

З

Рис. 2.32. Диаграмма напряжений в схеме на рис. 2.31

адача 2.11. Найти среднее значение выпрямленного напря­жения, ток нагрузки преобразователя 1ФШ2П (рис. 2.3) и постро­ить кривую напряжения u_d. Трансформатор и вентили идеальные.

Рис. 2.31. Управляемый преобразователь со схемой 1Ф1Н2П (задача 2.11).

Дано: U_si=U_s2=lQQ В, E_d=85 В, R_d=2 Ом, L_d=l4,6 мГн, а=€0°, /=50 Гц.

Решение. Угол выключения можно определить по номограм- мам на рис. 2.13. Используя данные задачи, получаем: E_d 85 _

д== VTu_s ^Г-ioo ⁼⁰'^6;

Rd 2

cos ф = г ■ —•—/ — w,4.

Ш + W К2² + (314.14,6-10-³)²

По номограмме для а=а'=60° определяем угол выключения:

Овыкл⁼⁼0^,выкл^185 .

Поскольку

авыкл—а<180°,

режим проводимости прерывистый. На рис. 2.32 приведены кривые выпрямленного напряжения и& и напряжения id&d на активном

сопротивлении (та же самая форма кривой, что й для тока i_d)-В интервале проводимости ток нагрузки определяется разностью Е_й и одного из напряжений и_а1 и и_е2. Среднее значение выпрямлен­ного тока может быть вычислено по среднему значению выпрям­ленного напряжения и противо-ЭДС Ed-

Н

^{[sin ( —J )-Sin (а --J) J +}

а основании уравнения (2.1) среднее значение выпрямлен­ного напряжения будет равно:

VTU_S

v_d = p-

^

а

•выкл'

^-j=[sin (185*—90»)—sin (60*-90^е)] + ₊ 85 (l - ^I85₁7₀⁶° ) = 67,2 -f 25,97 = 93.17 B.

a среднее значение тока нагрузки

V^—E_d 93,.17 —85 Rd ~ 2

=4,085 A.

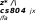LP Id

-Id

wt

Рис. 2.34. Диаграммы напряже­ний и токов в схеме на рис. 2.33 для ннверторного режима.

Задача 2.12. Преобразователь со схемой соединения 1Ф1Н2П Питает нагрузку, состоящую из резистора с сопротивлением R_d, реактора с индуктивностью L_d и противо-ЭДС E_d. Каково должно быть значение индуктивности L_d для обеспечения режима непре­рывной проводимости? Дано: U_s=Ue\~U_BZ=220 В, £d=62,5 В, /?<*=! Ом, <х=60°, f=50 Гц.

Определить среднее значение тока нагрузки. Трансформатор и вентили идеальные.

Решение. Значение индуктивности L_d, необходимое для обес­печения режима непрерывной проводимости, может быть получено по номограммам, приведенным на рис. 2.13. При а=60° и

_ ^Е* 62,5

проводимость становится непрерывной, если cos <р^0,2. Из этого условия определяем необходимую индуктивность:

cos _ R_d 1

COS*~VR*_d + (<>>Ld)* Kl + (314L_d)²~ ^,2j

Ld = '2i4^=s 15,62-Ю-³ Гн = 15,62 мГн.

Среднее значение тока нагрузки будет равно:

(J_s^s,'n~— cos а — V_dcosa—E_d ^я Р ^й

U =

Rd R_d

2

У~2 -220-— sin-|- cos60 — 62,5 = j =36,5 A.

Задача 2.13. Построить кривые и определить значения вы­прямленного напряжения, выпрямленного тока и токов сетевой и вентильной обмоток преобразовательного трансформатора в схеме 1ФШ2П, показанной на рис. 2.33. Трансформатор и вентили иде-ялъные, *_Tp = l_f U_s = U_8l = U_S2=100 В, £"_d=200 В, R_d=l Ом, Ld^oo, а= 150°.

Решение. Принимая во внимание значение угла управления («>90°) и полярность противо-ЭДС E_d, приходим к выводу, что преобразователь работает в инверторном режиме. Так как индук­тивность сглаживающего реактора велика, проводимость будет не­прерывной. Кривые напряжений и токов показаны на рис. 2.34. Выпрямленные напряжение и ток:

Vd^Udlo cos «= YTU_S -~ sin -j cos a = УТШ X

2 75