2.2. Задачи по однофазным преобразователям

Задача 2.1. Найти среднее значение выпрямленного напря­жения u_d для схемы выпрямителя, показанной на рис. 2.16, если Cd^oo, /?_d=l0 Ом, R=\ Ом, l/_s=110 В, f=50 Гц. Вентиль идеаль­ный. Построить кривую тока, .потребляемого от источника.

Решение. Поскольку Cd^oo, выпрямленное напряжение бу­дет сглаженным, в нем отсутствуют высшие гармони™ (рис. 2.17,а). Конденсатор потребляет энергию источника питания в интервале а-^ю^аг- разряжаясь затем в интервале aa^Q)/^ai-}-2ji. Кривая тока, потребляемого от источника питания, показана на рис. 2.17,6, где

/д.макс = (^2 U_s-U_d)/R. Напряжение (Та па нагрузке определяется из условия равенства зарядов, получаемых и отдаваемых конденсатором Са в течение каждого периода, т. е.

j (*д— id)dtat= j* itfderf.

Учитывая, что (рис. 2.17) *

/_д = -j^(VTU_s sin Ы — U_d), . Vd

u_d = V2 U_s sin a,

a, = (rc — 0)/2 и a₂ = (те-f 0)/2,

шосле интегрирования и упрощения получаем следующее уравнение:

U 8 8 \ J R

\8 2 ~ 2 ) п -R_d '

Таким образом, интервал проводимости диода зависит только •от отношения активных сопротивлений. Графическое решение полу­ченного трансцендентного уравнения приведено на рис. 2.18. В рас­сматриваемом случае

/?_d/j?= Ю/1 = 10 и 9 = 98°,

S

т

■30

о

50

500

O

в/г

N

Rd/H

0,1 0,5

Рис. 2.18. Диаграмма для определения интервала про­водимости диода.

тг. е.

^_d = ]/'2^_(7_ssina₁==V^r2"t/_ssin--9~==K2~-ll0sln41^o = 101,8 В.

Задача 2.2. Найти среднее значение выпрямленного напря­жения Ud в однофазной однонаправленной схеме идеального вы-•прямнтеля, показанной на рис. 2.19, амплитуду пульсаций выпрям-.ленного напряжения и обратное напряжение диода, если Cd= = 1000 мкФ, #4=100 Ом, Я=10 Ом, U₈=\10 В, f=50 Гц.

Решение. Данные задачи не удовлетворяют условию Cd^°°. •Однако так как C_d/?_d=10³- Ю"⁶- 10-=Ю,1» I/2f=0,01 с, приближен­ное решение может быть получено по графику на рис. 2.18. Для данной задачи Ra/R=l00/\—100, отсюда 8=50° и, следовательно,

U_d = V'2 U,

sin

-«=УТ.Ц0

sin

180 — 50

т. е.

t/_d=141 В.

Амплитуда пульсации может быть определена приближенно из рис. 2.20.

Будем считать, что конденсатор заряжается в течение интервала «времени, приблизительно равного интервалу проводимости в, и разряжается в течение оставшейся части периода.

Заряд конденсатора в процессе заряда увеличивается на

где Ui—приращение напряжения на конденсаторе d за время заряда. Разряд конденсатора происходит в интервале 2я—6, и уменьшение заряда в течение этого интервала приблизительно опре­деляется «как

Qi =

Ud 2^—I

Напряжение U\ .может быть вычислено из условия равенства получаемых и отдаваемых зарядов, т. е.

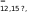
У

	■9			Izx jx

д 2п— I R_d. to

отсюда, амплитуда пульсации равна:

1 Ud 2п—В