
- •Москва энергоиздат 1982
- •Общие положения
- •Глава вторая
- •2.1. Подробный обзор
- •.Треугольник—шсстиФаз-иая звезда* с уравнительным реактором
- •С уравнительным реактором
- •Так вентильной обмотки
- •Поправь на коммутацию
- •Расчетная мощность
- •Как эквивалентного трансформатора
- •2.2. Задачи по однофазным преобразователям
- •2 Рис. 2.20. К расчету колебаний выходного напряжения в схеме на рис. 2.J9. 50 п - 2 RdCd to '
- •Xjslnj cos 150 « — 78 b;
- •2.3. Задачи по трехфазным преобразователям
- •2.5. Задачи смешанного типа
- •Первое приближение
- •2.6. Примеры для самостоятельного решения
- •Глава третья прерыватели переменного тока
- •3.1. Краткое описание
- •3.2. Задачи по однофазным прерывателям переменного тока
- •3.3. Задачи по трехфазным прерывателям
- •VtvTu I я V rrf"n
- •3.4. Примеры для самостоятельного решения
- •4.2. Задачи по прерывателям постоянного тока
- •11 Паке
- •4.3. Примеры для самостоятельного решения
- •Автономные инверторы
- •5.1. Общий обзор
- •5.2. Задачи ло автономным инверторам
- •1 Тпер "
- •Глава шестая защита силовых полупроводниковых приборов
- •6.1. Подробный обзор
- •В звезду.
- •V ' *s макс ш
- •15Р. Макс * sp- макс
- •1 Макс
- •Глава седьмая электронные схемы 7.1. Подробный обзор
- •Характеристики усилителей, выраженные через параметры четырехполюсников, внутреннее сопротивление источника сигнала и сопротивление нагрузки
- •Обратная сЗязь
- •RHj* fill*
- •Vljbk вых
- •7.2. Задачи по усилителям
- •7.3. Примеры для самостоятельного решения
- •7.4. Задачи по мультивибраторам
- •7.6. Задачи по стабилизаторам
- •Рас.Макс т4
- •Список литературы
- •Московская типография № 10 Союзполнграфпрома при Государственном комитете ссср по делам издательств, полиграфин н книжной торговли. 113114, Москва, m-u4, Шлюзоэая наб., 1р
1 Тпер "
'Т21Ср
1 I
/д»2Ср— /д22Ср 2 Т ^мЭкс 8 ~~~
1 1 п ю-ю-3 , _о .
10TTFT-2-25--8-- = l,563 А; ^Tiscp — /т22ср = /диср — 7,813 А;
Uicp = /rf'?cp = — 12»5 А.
щ
|
|
таг |
|
|
jj |
и.
1
,СГ71Г
' hi,in 1гг,
l/r-1 ' i i
2;
Рис. 5.32. Диаграммы характерных величин в схеме на рис. 5.31 при активной нагрузке.
Задача 5.8. На пары тиристоров 74—Ti, и 7г—Т$ однофазного мостового инвертора подаются управляющие импульсы со сдвигом по фазе на 90° с целью регулирования напряжения. Тиристоры заменены диодами и ключами (рис. 5.31). Построить кривые напряжения и и токов £д, in и id и найти средние значения токов, если £d=10 В, /=100 Гц и а) нагрузка R=\ Ом, б) нагрузка L=\ мГн. Вентили идеальные.
Решение. Разделив источник питания на два, будем отсчитывать напряжения относительно нейтрали. Напряжения Щц я «20 определяются исключительно состояниями ключей и обратными диодами (рис. 5.32,а, б). Напряжение
и—Що—«20 (рис. 5.32,в).
О
10
'макс ^
Обратные диоды не проводят ток. Ток тиристора показан на рис. 5.32,г. Среднее значение тока тиристора
1
1
=
2,5 А;
^т.ср
— 4
7|
макс л —
4~4
б) кривая тока i состоит из отрезков прямых с наклонами
~ЧГ=° и -
dt L
а
fмакс
—
ю
8
L
1-10-
= 12,5 А
'rf — '*т2 "Ь '-Ti — (*Д1 + 'дг)'
Средние значения токов:
/т!ср=/т2ср=/д2ср=/д4ср=3,906 А; /т2ср=Гт4ср==:/д1ср.=/дзср=0,781 А;
Id ср=0.
Задача 5.9. В схеме однофазного мостового инвертора (рис. 5.34) тиристоры заменены ключами, последовательно соединен-
Р
|
|
№ |
|
|
Ed |
t |
||||
1 |
|
|
|
а) |
||||||
/~1
гл
гл гл гщ±
ными с диодами, коммутирующий конденсатор Ск не используется. Построить кривую напряжения и и кривые токов id, iT и /д и найти средние значения токов, если Ей=Ю В, f= =100 Гц, £=1 мГн и =^со. Вентили идеальные, а активные сопротивления реакторов очень малы.
Р
*Л
i-дг д) N
ГЛ ГЛ
ГЛ ГЛ
та
t
A
in /_1
А
Аг>
повторения процесса, либо путем попытки предположения такой работы системы, которая на основе анализа одного периода удовлетворяет условию периодичности.
В рассматриваемом случае в поисках квазистационарного со- стояния помогает тот факт, что активное сопротивление нагрузки незначительно. Это оправдывает предположение о равенстве нулю среднего значения тока L По- скольку же LK^oof то ib может быть только идеально сглаженным постоянным током. Если в цепи коммутирующей индуктивности нет никакого активного сопротив- ления, то ib может в принципе быть на сколько угодно больше максимума тока нагрузки /иаис. Этот ток протекал бы по цепи, состоящей из тиристора в состоя- нии проводимости и обратного диода. Если же предположить, что некоторое активное сопротивление Рис. 5.34. Схема идеального имеется, то этот циркулирующий однофазного мостового инвер- ток будет демпфирован. Однако тора (задача 5.9). его значение не может быть на-
13* 195
много ниже /макс, так как в этом случае обратный диод будет закрыт, циркулирующий ток исчезнет, и напряжение, подаваемое на LK через тиристор, находящийся в открытом состоянии, увеличит ток, протекающий через LK, отсюда * = /Макс.
Средние значения токов, протекающих через отдельные элементы, и среднее значение тока, потребляемого от источника питания, могут быть определены в соответствии с рис. 5.35,а—е;
Т Ей 10-10-3
/макс — л, 7 —
10
1 • 10
—=25 А;
25
/т.ср =-о—=12,5 А;



 1
10-10-
1
10-10-
1
—=12,5 А;
Рис. 5.36. Схема непогруженного однофазного мостового инвертора без обратных диодов (задача 5.10).
t
2L« dt +UC0 + C
iddt = Ed,
где Uсо — напряжение па конденсаторе в момент включения. Это уравнение имеет следующее решение:
U=Id макс Sin (<ОоН-ф),
ТО 21^ "
Начальные условия
did Uсо
относящиеся к моменту t = О, дают:
Ed — Uco
откуда
Ed — Uco
Ч = - 9F ,л sint^'
Кривая (напряжения и на нагрузке определяется уравнением (рис. 5.37)
U=Ed~\- (Uс о—) cos <0ОГ.
Максимум напряжения на нагрузке равен:
UK&vc=&Ed—Uco-
Колебания, показанные на рис. 5.37, не распространяются дальше первой полуволны тока и соответствующей части кривой напря-
|
|
|
|
|
|
|
|
|
/TV? |
|
|
/ \ \ / |
/ |
t |
|
|
|
||
Рис. 5.37. Диаграммы тока и напряжения после'первой коммутации в инверторе на рис. 5.36.
жения (показаны на рисунке жирными линиями), потому что находящиеся в открытом состоянии тиристоры выключаются, как только ток становится отрицательным. В соответствии с данными задачи
(р
= —г
!/-=■>
I
===2,24-101
Ги-
Так как /о>г=Ю0 Гц, то тиристоры остаются закрытыми до конца полупериода, а затем процесс повторяется после включения следующей пары тиристоров. Квазистационариый режим не возникает, так как результирующее значение напряжения увеличивается на 2Ed за каждый полупериод (рис. 5.38).
Максимальное значение тока /макс увеличивается как арифметическая последовательность чисел 1, 3, 5 и т. д. После первого включения Imuuc=Eci/2Lk(x)q.
Непрерывное увеличение тока и напряжения препятствует применению этой схемы.
Задача 5.11. Построить кривые напряжения и и тока ib не-нагружешюго однофазного мостового инвертора (рис. 5.39), если Еа=10 В, /=100 Гц, 1 мГн, Ск=0,1 мкФ. Вентили идеальные.
Решение. Обратные диоды не допускают, чтобы напряжение и увеличилось выше Ed,; как только оно достигает значения Ed, одна из пар диодов включается ih поддерживает напряжение на этом уровне. Реактор LK закорачивается включенной парой диодов и проводящей нарой тиристоров, а его ток продолжает циркулировать в цепи, состоящей из этих элементов.
В момент /=0 любого полупериода начальные значения (например, когда пара тиристоров Т}—ТА включена) будут:
iL=tz.o и UQ=—Ed.
Дифференциальное уравнение, которое нужно решить, имеет
вид:
%£Vk rff2 ~Т"К — Erf,
где
г
u = UQ +
Решение:
где
u=Ed-\-A sin ((Оо'Ч-ф), 1
В соответствии с начальными условиями получим:
-
1и>
tg у = ; и Л =:
sin <f>
Если u=Ed, обратные диоды Дг и Д4 включены, а токи реакторов 1к замыкаются в контурах / и //. Напряжение на нагрузке определяется по уравнению
u=-\-Ed=Ed— sln<? ((Oofi+Ф), откуда момент включения диодов ti——ф/<о. 198



sin у = ■
tgr"
2Eda>0CK
дает ток, протекающий в короткозамкнутых контурах (после перезаряда конденсатора),
к М = }/i2L0+(2E(lb>CK)z.
Эта формула может быть обобщена для любой k-й коммутации, если записать ее в следующем виде:
fed. k)=ViZLk-l + Vtdb>0CK)\
Поскольку ibk>ib k-u циркулирующие токи, увеличивающиеся с каждой коммутацией (рис. 5.40), неограниченно возрастают (та-
—iv^Tr—I
ИР*
£tf f— 7-Нг-77 "Г
3 \l™ ^
fcf I
Рис. 5.41. Схема однофазного мостового инвертора с резисторами, демпфирующими циркулирующие токи (задача 5.12).
мим образом, эта схема также не имеет практического применения). Приведенное выше доказательство не относится к первому включению, так как и(0)=0 и *ьо=0. 'В этом случае
u=Ed (1—cos (Hot); u(tl)=Ed=Ed{l—cos <o0fi); Г1=я/2соо
и
ib(ti)=Ed(uoCK.
Задача 5.12. Определить потери при коммутации недогруженного мостового инвертора (рис. 5.41), если циркулирующий ток затухает до нуля к концу каждого полупериода и £d=10 В, f= = 100 Гц, Lk=\ мГн, Ск=1 м«Ф- Вентили идеальные. Определить
наименьшее значение сопротивления, при котором будет происходить затухание.
Решение. iB соответствии с задачей 5.11 мгновенное значение тока в конце коммутации будет:
к ft) «" VPlo+ (2С<*»0СК)* = 2ЕаЩСК,
поскольку /ьо=0.
Энергия, запасенная в индуктивности £к, равна:
или, обозначив
1
W°- 1^27^'
получим:
Эта энергия должна быть рассеяна в резисторах. Результирующие потери в двух резисторах при коммутации будут равны 2Х7ь.
Так как в течение одного периода происходит две коммутации, то общие потери за один период составят:
4lTr.=4£2dCK=4- 10s-1 • 10-6=4-104 Вт,
а средние потери равны:
^=-ут—=4.10-4-100 = 4- 10-а Вт.
Длительность коммутации определяется в соответствии с задачей 5.11 следующим образом:
ЕащСк ге* = ^ ->со.
Поскольку = 0, то
и, в соответствии с условиями задачи,
щ
=
•..
1
=
=~г-
1 l=2-24.
10"
с;
0 У2Ц£К К2-10-3-1-10-6
=
2-2-24-Ю*
^6
= 70tl
мке.
Время затухания циркулирующих токов должно быть не больше, чем
Т
~2 г, =5-10» — 0,07-Ю-8 = 0,43-Ю-3 с.
Благодаря наличию демпфирующих резисторов Як циркулирующий ток затухает экспоненциально. Считая, что за время, равное
пятикратному значению постоянной времени, ток уменьшается практически до нуля, можно определить значения этой постоянной Гц и демпфирующего сопротивления следующим образом:
2 * 0,43 7'к= 5 =—=0,086 мс;
Як = ~-=\\,6 Ом. у к
Это, конечно, только приближенный расчет, так как при ic(r,)=2£dtDoCK=0,448 А напряжение на демпфирующем резисторе было бы равно: £/я=/к(/|)/?к=5,2 В. ^ Отсюда следует, что на самом деле этот процесс более сложный, так как напряжение UR препятствует нарастанию циркулирующего тока.
Lk/2
I*.
t-
I feJJ
Рис.
5.42. Схема однофазного мостового
инвертора, работающего на активную
нагрузку (задача 5.13).![]() З
З
AUT=AUa^\ В.
Р
_
1
макс,
к 20
*
макс— г
—
in
--^»
/
= ^-=,10 А;
/ - 10
Значения С*к и L*«, соответствующие /*макс=2, в соответствии с рис. 5.12 равны: £*к=2,15 и С*к=1,85, т. е.
L#=BnocV**=l -50- 10-в-2,15=107,5 мкГн. Эта индуктивность должна быть распределена на два полумоста, т. е. £к/2*=бЗ,75 мкГн.
Емкость коммутирующего конденсатора
Ск=С*кГВОс./^1,85-50 10-6=92,50 мкФ.
Следует отметить, что Нельзя существенно снизить емкость конденсатора путем увеличения LK.
Введение обратных диодов не оказывает влияния на время, предоставляемое для восстановления запирающей способности тиристоров, т. е. контур коммутации будет и в этом случае работать удовлетворительно.
Ток, протекающий через обратные диоды в момент их включения (при и=Ей), равен:
/д (0) ~ ^макс.к
Можно доказать, что ток, протекающий через индуктивность LK, становится равным /т.маис в момент, когда обратные диоды включаются. Через диод проходит ток, равный разности между током через индуктивность LK и током нагрузки:
/макс.к—/д(0)=20—10=10 А.
Время затухания циркулирующего тока, который проходит через индуктивность LK/2, закороченную обратным диодом и включенным тиристором, и демпфируется напряжением, равным 2AUT, составляет:
Уд(0) 107,5-10 Т
h
■=
4
=—47] =268,5
мкс < —.
Задача 5.14. Однофазный мостовой инвертор с обратными диодами работает на постоянную нагрузку L=10 мГн. Время восстановления запирающей способности тиристоров Гвос^бО мкс, а их допустимый максимальный ток /макс.к=3,5 А. Определить параметры цели коммутации при £d=10 В и f=100 Гц.
Проверить, обеспечивает ли падение напряжения Д1/т=А^д— = 1 В на диодах и тиристорах достаточное затухание циркулирующих токов.
Решение. Задача решается при помощи графиков, представленных в начале главы. Вычисления, подобные выполненным в задаче 5.1, дают:
/ = /макс — 2»5 А;
»* /макс.к 3.5
* макс.к— / —2,5—
iB соответстви с рис. 5.13 значения С*к-и £*к, соответствующие максимально допустимому выбросу тока, равны:
С*к=*2,5; Z.K=4.
Поскольку
О* Ed 10 Л Л.
имеем:
c<=ia^=iw
=26,9
мкф;
1К = 1%ШвшШ= 4-4-50-10-в = 800 мкГн.
Время, требуемое для затухания циркулирующего тока, находится, как и © предыдущей задаче, следующим образом:

где /д(0) = /,
Ас/д (0) 4Д(/Т
/= 1,0 А, т. е. 800-10
-47т—=2000 мкс;<—•
Задача 5.16. Инвертор с параллельной схемой выключения тиристоров (рис. 5.43) работает на нагрузку R=l Ом. Коэффициент трансформации трансформато- .
pa kTP—ws/Wp = 2, время восстановления запирающей способности тиристора ГВОс = =25 мкс. Определить параметры цепи коммутации, если максимально допустимый ток тиристоров /мако.к—80 А.
Проверить, достаточны ли напряжения 'AUT—AVn~\ В тиристоров -и диодов для затухания циркулирующих токов. Трансформатор идеальный, Ed=10 В, /=100 Гц.
Решение. Если тиристор Tz находится в открытом состоянии, а коммутация начинается при включении тиристора Т\, то можно считать, что схема присоединена к источнику питания в точках А и В. Двухполюсник, состоящий из трансформатора, резистора \R и конденсатора Ск (рис. 5.44), описывается следующими уравнениями:
ах ■■= uc/2; u = u.xWsfWp = uxkT^\ it-i2-ikTp = 0;
C~dT]
и
Т9
Из этих уравнений получаем:
Ц — 4Ск ~dt~' R ТР*
Отсюда следует, что двухполюсник может быть заменен параллельно соединенными конденсатором с емкостью Сак»**=4Си и рези стором с сопротивлением /?экв=^/^2тр-

Рис. 5.44. Эквивалентная схема цепи коммутации инвертора на рис. 5.43 при активной нагрузке (к задаче 5.15).
В
:40
А;
V3KB
т. е. /*
< 80_
- 40 -2-




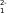
fмакс —;'
-exp(-"2T-)
1+ехр
100 1^ехр( —0,5)
2,5 1 + ехр( — 0,5) =9'82 А'
L
10
так как Т = 0,01 с; т = -^-=-
=0,01 с.
Учитывая быстроту процесса комимутацин, нагрузка, состоящая из последовательно соединенных резистора и индуктивности, может

Рис. 5.45. Эквивалентная схема цепи коммутации инвертора на рис. 5.43 при последовательном соединении активного сопротивления и индуктивности нагрузки (к задаче 5.16).
рассматриваться для этого процесса как чисто индуктивная. Относительные значения составят (см. рис. 5.13):
20
лаке — / 3 о йо ~-' 'макс з.о^.
L*K = 2; С*экв — 2,35.
Поскольку
макс
'00 . Л ^-^32 =10,19 Ом,
то имеем:
£к = ffi«d>*& =-■ 10,19.25-2 = 509 мкГн;
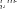 Смев
—'
Смев
—'
50-2,35 ^г~3" 10,19
= 11,55 мкФ;
=2,885 мкФ.
Циркулирующий ток /д(0)=9,82 А. Длительность процесса затухания этого тока равна:
4 = W|(p=i09^82 = 2500 MKc:<7,/2_
Таким образом, затухание циркулирующего тока удовлетворительное.
Задача 5.17. Инвертор с параллельной схемой выключения тиристоров (рис. 5.46) работает на чисто активную нагрузку с со-
205
 Рис.
5.46.
Однофазный
инвертор со схемой выключения
тиристоров параллельного типа и
обратными диодами, присоединенными
к ответвлениям обмотки трансформатора
(задача 5.17).
Рис.
5.46.
Однофазный
инвертор со схемой выключения
тиристоров параллельного типа и
обратными диодами, присоединенными
к ответвлениям обмотки трансформатора
(задача 5.17).
J
1 гт2
J
фициент трансформации транс- Ed форматора &Тр=2, время вос-
становления запирающей способности тиристора Гвос = =25 мкс. Определить параметры цепи коммутации, если до-—О пустимый максимальный ток
ТИрИСТОра /макс.к=40 А.
Коэффициент трансформации ответвления трансформатора &отв=оу р/шР=0,9б. Проверить, достаточно ли напряжение на этом ответвлении для демпфирования циркулирующего тока. Трансформатор и полупроводниковые элементы идеальные, £d=100 В, f— =500 Гц.
Решение. Коэффициент трансформации на ответвлении не влияет на время, предоставляемое для восстановления запирающей способности тиристора, .и поэтому вычисления могут производиться так же, как, например, в задаче 5.15. Находим:
R |
20 |
|
= 4 |
Eg _ |
100 |
^экв |
5 ~ |
макс.к |
40 |
|
~ 20 " |
С
Сэкв
— '
С якв^вос 1»^б * 25
= 9,25 мкФ;
: 2,31 мкФ.
Перезаряд коммутирующего конденсатора заканчивается, когда
% и в -2Е*
-2~kOTD = Ed, т. е ис т—
Если включился тиристор Т\, то обратный диод Д\ включается и возникает циркулирующий ток (рис. 5.47). В этом случае
УслОВиеМ равновесия Намагничивающих сил является
т. е.
(1 —ko т в ) /х,—f-feo roid—(/гтр=0,
отсюда циркулирующий ток равен
, % . .
lL — ld = g — * % '
"-OTB "•от в
где 1ь — ток в обмотке LK в момент включения обратного диода Д|. Так как
^тр Ед
то
1
40
d
0,95
on п осг == 20 А.
20 0.952 Демпфирующее напряжение равно: 1 ^отв
/1 — 0^5 \
^дем — &d '
 Время
затухания циркулирующего тока Cl
—WAk
_
20-268,5
Время
затухания циркулирующего тока Cl
—WAk
_
20-268,5
'
_1_
1
'2-500
Т_ 2
1032 мке;
Таким образом, теоретически демпфирование недостаточно. Однако на практике оно будет удовлетворительным, так как в приведенных выше вычислениях не учитывались падения напряжения на диодах и тиристорах и активное сопротивление демпфирующей цепи. Учитывая только падения напряжения на тиристорах и диодах и предполагая их равными Д£/Т==ДГ/Д===1 В, находим:
£/„вм=5,2+2-1=7,2 В
и
2
4
=
7,2
:745 мке.
В представленном в этой задаче решении не вся энергия циркулирующего тока рассеивается в виде тепла. Часть этой энергии возвращается в нагрузку через обмотку трансформатора. В результате улучшается КПД инвертора.
Задача 5.18. Трехфазный инвертор с последовательной схе-мой выключения тиристоров (см. рис. 5.10) питает индуктивную нагрузку, соединенную в звезду. Определить параметры коммутирующих конденсаторов Ск и индуктивности цепи коммутации LK, если £d=100 В, fc=100 Гц, L=10 мГн и *Лос=50 мке.
Решение. Схема работает подобно идеальной схеме, описанной в задаче 5.5 (см. рис. 5.25). Соответственно формулы, указанные в задаче 5.5, могут использоваться для нахождения максимального коммутируемого тока. Максимальный коммутируемый ток /макс определяется в соответствии с рис. 5.27 следующим образом:
2 / Ёа 2 10-10-8 100 'макс— * з 12 L — 2 з \2 10-Ю-3 —И'Н А.
Поскольку во время коммутации ток нагрузки изменяется незначительно, трехфазная схема при рассмотрении процессов коммутации может быть разделена на три однофазные и элементы цепи коммутации могут рассчитываться так же, как для схемы на рис. 5.3.
В соответствии с порядком расчета, изложенным в начале главы, находим:
#*=Яа//макс=Ю0/11,П=9 Ом. Подставив /макс.к//макс=^2, получим (см. рис. 5.13): Z.*k=2; С*к=2,37
и, следовательно,
1к*= #%ю<Х*к = 9.50-2= 900 мкГн; Ск = CVbqc/^* 2,37-50/9 = 13,17 мкФ.
Индуктивность одной половины спаренного реактора должна быть вдвое меньше вычисленного значения LK.
Задача 5.19. Однофазный инвертор со схемой, представленной на рис. 5.8, питает индуктивную нагрузку с незначительным активным сопротивлением. Тиристоры управляются таким образом, что кривая напряжения на нагрузке соответствует кривой, показанной на рис. 5.16. Вообще же система управления такого инвертора может обеспечивать коммутации в отдельных ветвях в разные интервалы времени, при этом исключается взаимное влияние коммутаций в различных ветвях. Определить параметры цепи коммутации, если £d=10 В, L=l мГн, f=»100 "Гц и /Вос~50 мке.
Решение. Определение параметров производится так же, как указывалось в начале главы. Было отмечено, что обычно при- нимают В0=\ (это приводит к оптимальным параметрам элементов цепи коммутации). В этом случае (см. рис. 5.14) В0 1
arctg#0 arctgl ~" Ь2732.
Максимальный коммутируемый ток нагрузки для таких же, как в данной задаче, условий был вычислен в задаче 5.1: /Макс=25 А. Используя приведенные в начале главы формулы, получаем:
Ск=
В;
R „
!127з2^
= 159,16 мкФ;
K arctg£0 Ed 10
^-'"ircipre ^,.2732^-° = 25,46 мкГн.
За мечание. Основная цель авторов при составлении рассмотренных задач состояла в содействии более глубокому пониманию теории инверторов. Именно поэтому здесь не рассматривались некоторые вопросы, требующие более тонкого анализа, без которого нельзя обойтись при определении параметров реального инвертора. Например, параметры контура выключения всегда определялись для нагрузок в установившемся режиме. В действительности же переходные процессы во время включения инвертора и резкие изменения нагрузки могут привести к появлению токов нагрузки, отличающихся от токов в установившемся режиме и превышающих нх. Поэтому параметры цепи коммутации должны быть соответствующим образом изменены по сравнению с требованиями установившегося режима.
I

Рис. 5.48. Однофазный инвертор со схемой выключения тиристоров параллельного типа и фильтром, присоединенным к его выводам
(задача 5.20).
Указанные замечания учтены в решении задачи 5.20.
Задача 5.20. Преобразователь со схемой соединений, представленной на рис. 5.48, работает на нагрузку, состоящую из последовательно соединенных резистора и реактора. Определить параметры фильтра и цепи коммутации, а также уровень затухания циркулирующих токов. Элементы схемы идеальные. Обратные диоды присоединены к ответвлениям от 5% витков обмотки трансформатора. Дано: £d = 48 В, напряжение на нагрузке Г/н = 220 В, /= =50 Гц, ток нагрузки /=5 А, коэффициент мощности нагрузки (coscp) изменяется в пределах от 1 до 0,866, fBoc=50 мкс. Амплитуда любой гармоники напряжения на нагрузке не должна превышать 3% амплитуды этого напряжения.
Решение. Проанализируем работу фильтра без нагрузки. Фильтр состоит из последовательного и параллельного резонансных контуров LSCS и LpCp. Далее для простоты омическими составляющими индукпивностей и емкостей будом пренебрегать. Однако при точном расчете параметров фильтра этими активными сопротивлениями пренебрегать нельзя.
14-9 209
Последовательный и параллельный резонансные контуры" должны быть настроены на резонанс при основной частоте. Чрезмерного падения напряжения на фильтре можно избежать путем настройки последовательного контура, а протекания чрезмерно большого тока через инвертор— путем настройки параллельного контура [38]. Обозначим реактивные сопротивления элементов LE, Св, Lp и Ср через
Xsl, ХцС, XpL, ХрС-
Условие резонанса в последовательном и параллельном контурах:
Xbl—Xsc и Хрl=Xpc-
Полное сопротивление настроенного последовательного резонансного -контура для я-й гармоники
zsn=i -jrxsc(n2 — О-
Полное сопротивление настроенного параллельного резонансного контура для я-й гармоники
*рп— я2 —1 '
•Коэффициент фильтрации фильтра для я-й гармоники равен отношению действующих значений напряжений иа нагрузке и на трансформаторе:
Sn = -7
Zsn Л" Zpn
Подставив' выражения Zsn и Zpn в эту формулу, находим:
XsC
Таким образом, сдвиг фазы на фильтре равен нулю или 180°, что соответствует предположению об идеальности элементов цепи. Другими словами, коэффициент фильтрации выражается положительным или отрицательным вещественным числом.
Знаменатель полученного выражения — многочлен четвертой степени. Приравнивая знаменатель нулю и находя корни v2i и v% биквадратного уравнения, можем представить коэффициент фильтрации в виде
я2
^""(я2 —>2,)(я2 —v22)*
Корни vi и V2 зависят от ХвС и Хрс и удовлетворяют условиям 0<vi<l и V2>1. Зависимость коэффициента фильтрации от частоты качественно показана на рис. 5.49. Видно, что фильтр усиливает гармоники с номерами Vi и v2, поэтому его параметры должны быть так выбраны, чтобы значения Vi и Vs не совпадали ни с одной из гармоник спектра, генерируемого инвертором. С учетом этого наиболее рациональной последовательностью выбора фильтра является следующая: выбираем емкость Св предпочтительно малой (ограничением является падение напряжения на конденсаторе, когда через него будет протекать полный ток нагрузки /). Реактивное сопротив-
ление фильтра XsC можно вычислить по максимальному току нагрузки и номинальному напряжению конденсатора;
индуктивность Ls находится из условия XsCr=XaL;
по заданному значению коэффициента фильтрации sn вычисляется отношение kn=Xec/XPc, что в свою очередь позволяет определить значение ХаС;
индуктивность Lp определяется из условия ХРс=ХРь',
для полученных таким образом значений вычисляются относительные резонансные частоты Vi и V2- Далее проверяется, достаточно ли они далеки от гармоник, содержащихся в выходном напряжении. Если результат неудовлетворителен, следует сделать поправку.

*ТР |
|
U тр. макс |
|
|
|
|
|
|
|
|
|
|
г/г |
Г |
ЗГ/2 |
Рис. 5.50. Диаграмма напряжения на трансформаторе в схеме инвертора, изображенной на рнс. 5.48.
Определение параметров фильтра для характеристик нагрузки, приведенных в задаче. Как и в предыдущих задачах, можно считать, что от инвертора на трансформатор подается приблизительно прямоугольное напряжение (рис. 5.50). При отсутствии нагрузки действующее значение составляющей напряжения основной частоты на выходе трансформатора должно быть равно Г_/тр]=220 В, откуда ее максимальное значение
^тр. макс = 2201^2"= 311 В.
Из разложения напряжения прямоугольной формы в ряд Фурье следует:
Цгр.макс~ U-rpi макс — "4 311 = 244,2 В.
Амплитуды высших гармоник напряжения при этом будут равны:
^трэ макс =ЮЗ,8 В; 0^,»*—в2,2 В; Г7ТП7 макс = 44,4 В; Urpsмакс — 34,88 В; £Агри макс—28,3 В; С/тр13 макс == 23,85 В; £>тР1бмакс = 20,45 В; £/тр17макс = 18,31 В.
В общем случае на коэффициент фильтрации влияет также нагрузка. При указанной в задаче нагрузке это влияние незначительно, поэтому далее мы будем рассматривать характеристику фильтра без учета нагрузки.
Из рис. 5.49 видно, что достаточно выбрать параметры фильтра по условию фильтрации гармоники низшего порядка (третьей). До- пустимое значение VSH&KC в соответствии с условиями задачи мо- U* 211
жет быть установлено равным:
3 _2-220
^змакс— ^макс jQQ jqq 3 — 9,33 в.
Коэффициент фильтрации для л=3 будет отрицательным (см. рис. 5.49):
^змакс — 9,33
ss = tj — ,03 о = —0,0901.
•^трэ макс ivo,o
Формула для коэффициента фильтрации может быть представлена в виде
Подставив значения s3, получим:
З2 / 1 \
ks = (32 — 1)2 ^3 — —0,0901 у ^
Допустим, что используются конденсаторы с номинальным напряжением переменного тока 220 В, что определяют максимально допустимое значение Хвс как
220 220 Л
Следовательно, минимально допустимая емкость будет: 10е 106
с* = 1^= 314^44 ==72'35 мкФ"
Ближайшее стандартное значение емкости Св=75 мкФ, и, следовательно,
1 106
Условие резонанса предполагает, что
^- = ^ = 42,4 Ом.
т. е.
(О
По условию фильтрации
т. е. Ср=С8йз=72,35-1,702=123,2 мкФ, 212
Выберем ближайшее стандартное значение Cj,= l25 мкФ, тогда из условия резонанса получим:
_ 1 106
ЛрС = XpL = с
откуда
^ 25,45 Л Л ^ 314-=0,0в1 Гн.
Сравним полученное значение коэффициента фильтрации с необходимым значением:
ss— _ 42,4/25,45(З8 — 1)2-f З8 ~ —0,0906.
Сравнение показывает, что эти значения расходятся незначительно.
Для проверки вычислим резонансные частоты. Значения V| и v?. представляют собой корни многочлена в знаменателе выражения для 8s». Решение уравнения
-V— (/г2 — l)2-f я2 = 0
ЛрС
дает
Подставив параметры фильтра, получим:
2
f
/
25,45 \2
У
(1+2T2T4J-
1+2^4274 ±1/ f l + tt-l) "I =1.3 ±0,83,
откуда Vj=0,685, чему соответствует критическая частота 40,2 Гц, и va= 1,458, чему соответствует критическая частота 72,9 Гц. Оба значения достаточно далеки от частот нечетных гармоник, возникающих в идеальном случае в напряжении с7тр, и от частот четных гармоник, которые могут появиться при асимметричных режимах работы инвертора.
Анализ коммутации в инверторе. Для такого анализа необходимо построить кривую тока iTp, протекающего через выходной трансформатор инвертора.
Ток iTp состоит из основной составляющей £тр, обусловленной током нагрузки, и высших гармоник тока £Тр:
СО
n-l
где i'Tpi =&
Оценим амплитуды высших гармоник тока.
Из сделанных вычислений видно, что коэффициент фильтрации для п=3 равен:
S3=—0,0906,
т. е. третья гармоника напряжения на выходе фильтра уменьшается приблизительно в 10 раз.
С
U.
трп
UTpn
4-^^-1)
П
*'тра
— ]
^^5С(32-1) -т-42.4(9-1)
= 0,648 А;
V.
трв
макс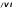 6
6
/тре — j
И=~*с(52-1) -г 42,4(25- 1)
= 0,2165 А.
и
и
1накс
7![]()
t
2-3
г-з
L
i-TP
LTZ3
<-Г7Л![]() а
а
ю

г)
М . д)
*Af,« LA2,3
ГУ М. h
Рис. 5.51. Диаграммы токов и напряжений для установившегося режима работы инвертора по схеме на рис. 5.48,
Отсюда видно, что амплитуды рассчитанных гармоник тока не превышают 15% тока нагрузки /, поэтому ими можно пренебречь, когда проводится анализ цепи коммутации.
Иа рис. 5.51 показаны кривые напряжений и токов инвертора. Кривые а, б и в относятся к чисто активной нагрузке, кривые а, г, д и е — к нагрузке, состоящей из активного сопротивления и индуктивности. При изображении кривой напряжения на нагрузке и тока инвертора влияние высших гармоник не учитывалось. Не отражены также процессы коммутации (т. е. предполагалось, что коммутация происходит мгновенно).
Определение параметров цепи коммутации. Индуктивность последовательного резонансного контура Ls настолько велика, что можно считать ток нагрузки tTp инвертора постоянным в течение всего процесса коммутации. Для расчета параметров цепи коммутации иеоб-
хбДимо в качестве исходных данных звать наибольший возможный ток через тиристор в момент, непосредственно предшествующий коммутации.
Из рис. 5.51,5 видно, что непосредственно перед коммутацией ток тиристора меньше максимального тока нагрузки, отнесенного к первичной обмотке трансформатора.
Было бы совершенно неправильным определять параметры цепи коммутации для этого тока, т. е. во время переходных процессов могут возникнуть гораздо большие токи.
Учитывая сложность задачи, лучше всего проводить исследование поведения системы в переходных процессах методами аналогового или цифрового моделирования.

* U
Рис. 5.52. Диаграммы токов и напряжений для переходного процесса после включения инвертора по схеме на рис. 5.48.
Рассмотрим пример включения инвертора на номинальную нагрузку (cos <р=0,866). На рис. 5.52 показаны кривые напряжения «тр на трансформаторе напряжения на выходе инвертора и, напряжения на последовательно включенном конденсаторе «св и тока нагрузки инвертора is-
Видно, что напряжения на последовательно включенном конденсаторе могут значительно превышать напряжения, возникающие в установившемся режиме, поэтому следует выбирать номинальное напряжение конденсатора значительно большим напряжения, вычисленного для установившегося режима.
Наибольший коммутируемый ток, отнесенный к стороне нагрузки, равен приблизительно семи или восьми амперам. Будем с запасом считать его равным десяти амперам.
Коэффициент трансформации трансформатора равен: t/тр.макс 244,2
Таким образом, получаем:
/т==^тр/тр.макс=5,09-10=50,9 А;
^*=£d//T=48/50,9=0,944 Ом.
Будем считать допустимым, что максимальный ток тиристора в интервале коммутации в 2 раза превышает наибольший коммутируемый ток, т. е. /*макС.к==/т.ыакс.к//т.макс=2, тогда в соответствии с рис. 5.13 получим:
1*к=2 и С*к=2,4,
т. е.
Lk = £*к/?*гвос = 2-0.944-50- 10-в = 94,4 мкГн;
2
4-50-10-6
CK=C*KtBOC/R*
=
q>Q44—
= 127 мкФ.
Проверка затухания циркулирующего тока. Поскольку обратные диоды присоединены к ответвлениям от 5% витков обмотки трансформатора, демпфирующее напряжение равно:
LW=£dOr05=48- 0,05=2,4 В.
Циркулирующий ток (см. задачу 5.16) равен:
/Д'(0)=50,9 А.
Время затухания циркулирующего тока равно:
•Мд(О)
94,4-10 - 6-50,9
3' 2-2,4
=
1000-10-* = 1000 мкс,
т. е. г3<7/2=10 мс.
Таким образом, можно считать, что циркулирующий ток затухает удовлетворительно.
