Расчетное задание Вариант 1

Задача 1. Определение вероятности событий.

На кубиках нанесены цифры от 0 до 9. Последовательно случайным образом извлекают 2 кубика. Какова вероятность того, что на первом кубике цифра будет меньше 3, а на втором – больше 6?

Задача 2. Правила сложения и умножения вероятностей.

В урне 4 шара, пронумерованные цифрами 1, 2, 3, 4. Извлекают первый шар, записывают номер, затем – второй. Опишите: а) пространство элементарных исходов, представляющих двузначные числа из различных цифр; б) событие = {число делится на 2}; в) событие = {число делится на 4}; г) событие = {число делится на 3}. Являются ли эти события попарно несовместными? Вычислите: .

Задача 3. Условная вероятность. Формула полной вероятности. Формула Бейеса.

Имеется 5 винтовок, из которых 2 – с оптическим прицелом. Вероятность попадания в цель при выстреле из винтовки с оптическим прицелом составляет для данного стрелка 0,95; без оптического прицела – 0,8. Найти вероятность попадания в цель, если стрелок сделает один выстрел из наудачу взятой винтовки.

Задача 4. Повторение испытаний. Формула Бернулли. Локальная и интегральная теоремы Лапласа.

1. Монету бросают 5 раз. Найти вероятность того, что герб выпадает не менее четырех раз.

1. Среди семян ржи – 0,4 % семян сорняков. Какова вероятность при случайном отборе 500 семян обнаружить 5 семян сорняков?

2. Производится стрельба по цели. Вероятность попадания при одном выстреле - . Производится 100 выстрелов. Какова вероятность того, что цель поражена в большинстве выстрелов?

3. Сколько нужно взять деталей, чтобы наивероятнейшее число годных было равно 50, если вероятность того, что наудачу взятая деталь будет бракованной, равна 0,1? Какова вероятность появления 50 годных деталей в указанной партии?

Задача 5. Дискретная случайная величина.

В партии, состоящей из 10 деталей, имеется 4 бракованных. Наугад извлекают 3 детали. Составить закон распределения случайной величины , представляющей собой количество бракованных деталей среди 3 выбранных. Вычислить математическое ожидание случайной величины , дисперсию , среднее квадратичное отклонение , а также начертить многоугольник распределения и график функции распределения.

Задача 6. Непрерывная случайная величина.

Случайная величина задана функцией плотности распределения . Найти:

1. Функцию распределения и необходимые константы.

1. Математическое ожидание, дисперсию и среднее квадратичное отклонение.

2. Вероятность попадания случайной величины в интервал .

Построить графики функции плотности распределения и функции распределения :

.

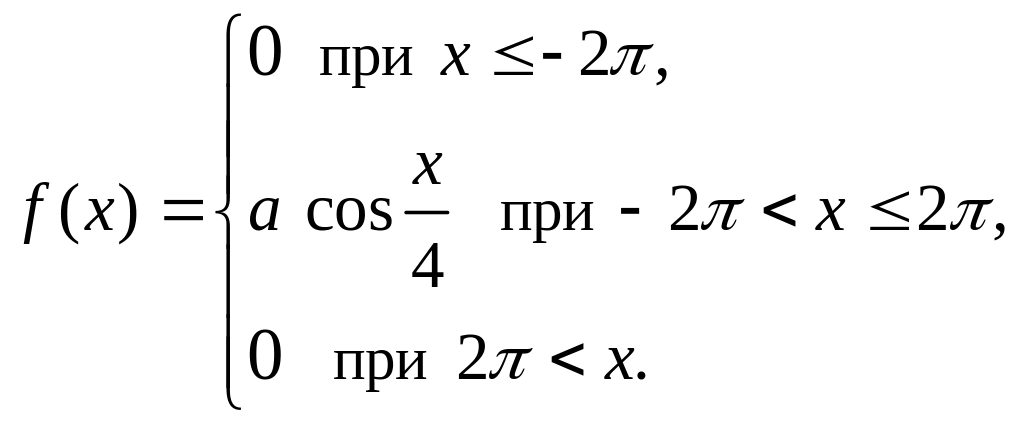
Задача 7. Найти выборочное уравнение прямой линии регрессии У на Х и оценить тесноту корреляционной связи для случайных величин, приведенных в таблице

	5	10	15	20	25	30
10 20 30 40 50	3 - - - -	5 4 - - -	- 4 7 2 -	- - 35 10 5	- - 8 8 6	- - - - 3	8 8 50 20 14
	3	9	13	50	22	3