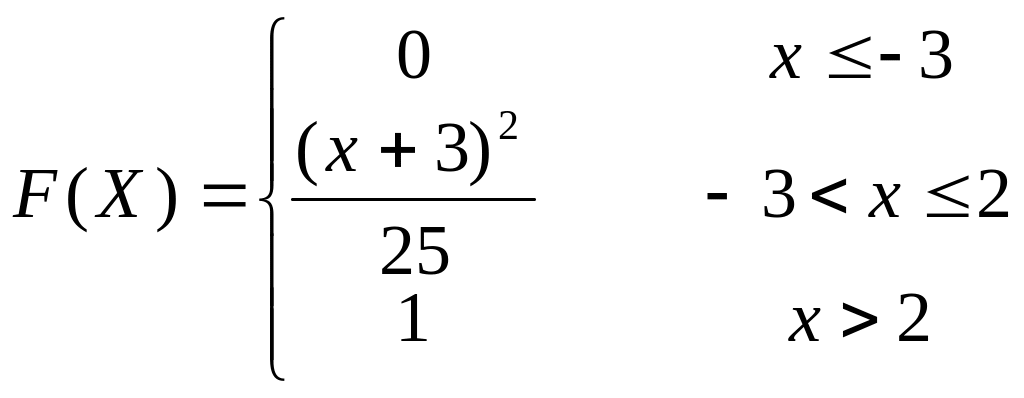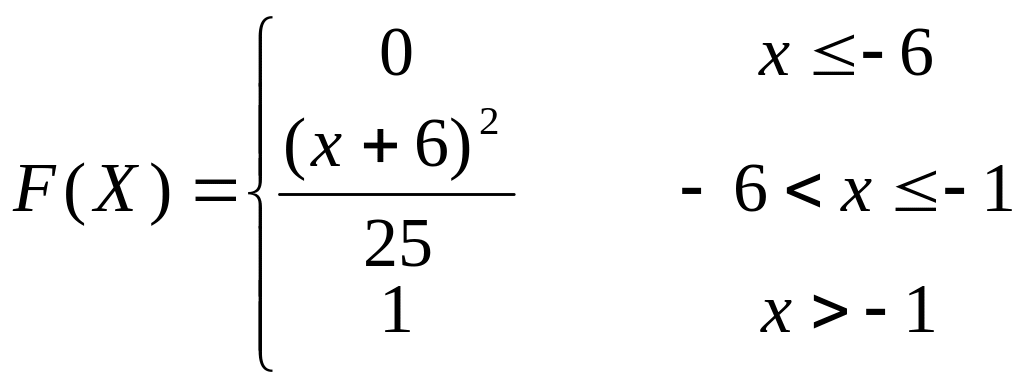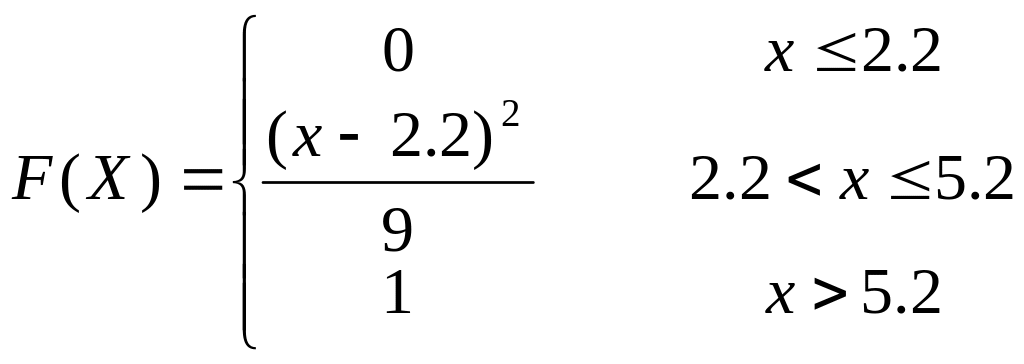Глоссарий

Благоприятствующее элементарное событие. Элементарное событие, при наступлении которого наступает событие А, называется элементарным событием, благоприятствующим событию А.

Вероятность — числовая мера правдоподобия события. Вероятность прини­мает значения от 0 до 1.

Выбор наудачу (случайный выбор) — выбор одного предмета из некото­рого набора, при котором шансы на выбор любого предмета одинаковы.

Выборка — часть всей совокупности людей или предметов, отобранная для исследования. Например, выборкой является группа избирателей, которую опрашивают для предварительного выяснения шансов кандидатов на избрание в парламент страны.

Демография — наука о закономерностях изменения численности и состава населения.

Диаграмма — метод графического представления данных, который исполь­зуется для наглядного их отображения и сравнения. Как правило, диаграммы не дают точных значений, но лишь приблизительные.

Диаграмма круговая — диаграмма в виде круга, разделенного на секто­ры. Каждый сектор показывает, какую долю целого составляет та или иная величина в наборе данных. Обычно круговые диаграммы применяются для изображения состава населения, деления экономики на отрасли и т. п.

Диаграмма рассеивания — диаграмма, составленная из точек на коорди­натной плоскости. Диаграммы рассеивания применяются для изучения связей между различными характеристиками, например ростом и весом животного и т. д. Абсцисса и ордината каждой точки — значения этих характеристик.

Диаграмма столбиковая — диаграмма, наглядно показывающая соотноше­ние между различными значениями. Каждое значение представляется в виде столбика, высота которого пропорциональна этому значению.

Диаграмма Эйлера — способ графического изображения событий в виде фигур на плоскости. Каждое событие изображается некоторой фигурой, пере­сечение событий — общей частью этих фигур, объединение событий — объеди­нением фигур. Диаграммы Эйлера позволяют наглядно показать связь между различными событиями. Несовместные события изображаются фигурами, не имеющими общих точек.

Дисперсия случайной величины — мера рассеивания (разброса) значений случайной величины, определяемая формулой

D(X) = E(X – E(X))².

Дисперсию также можно вычислять по формуле

D(X) = E(X²) – E²(X).

У постоянной случайной величины дисперсия равна нулю.

Дисперсия набора чисел — мера разброса значений числовых наборов (чи­словой выборки). Дисперсия набора равна среднему квадрату отклонения чисел набора от среднего арифметического значения:

=

Достоверное событие — событие, вероятность которого равна 1. Это собы­тие обязательно происходит при проведении опыта. Примером достоверного события является событие «выпал либо орел, либо решка» при бросании мо­неты.

Событие, противоположное достоверному, называется невозможным.

Дюйм — мера длины, равная 2,54 сантиметра. Один фут состоит из 12 дюй­мов. Один дюйм равен 10 линиям. В дюймах и линиях, например, измеряется калибр оружия. Знаменитая винтовка Мосина называется трехлинейкой, по­скольку имеет калибр 3 линии, т. е. 7,62 мм. Трехдюймовка—орудие, имеющее калибр три дюйма — 76,2 мм.

Футы и дюймы — основные единицы измерения роста людей, длин и высот сооружений в США.

Закон больших чисел — собирательное название группы математических теорем, утверждающих, что среднее значение суммы случайных величин мало отличается от среднего значения их математических ожиданий при различных условиях. Основное условие — большое число складываемых величин, откуда и происходит название закона.

Испытание Бернулли—эксперимент, который заканчивается одним из двух элементарных событий: успехом или неудачей.

Комбинаторная задача — задача, связанная с необходимостью перечисле­ния предметов или их комбинаций.

Легенда диаграммы — изображение условных обозначений с разъяснения­ми. Легенды также бывают у географических карт.

Маловероятное событие — событие, вероятность которого в обычных усло­виях считается малой. Пример — выигрыш в лотерею.

Математическая монета — «идеальная» монета, которая падает вверх орлом с вероятностью . Все свойства настоящей монеты — размер, материал, достоинство — для математической монеты несущественны. Математическую монету еще называют симметричной монетой.

Математическая игральная кость — «идеальный» игральный кубик, для

которого вероятность выпадения любой грани равна . Математическую кость называют также симметричной. Наилучшим приближением к математической кости является обычная правильная кость.

Математическое ожидание случайной величины — числовая характери­стика случайной величины, показывающая ее среднее значение. Математиче­ское ожидание случайной величины вычисляется по формуле

Е(Х) = + + …+ ,

где — вероятность того, что X= .

Медиана числового набора. Медиана набора — число, которое характери­зует расположение набора на числовой прямой.

Чтобы найти медиану, набор чисел можно упорядочить по возрастанию. Если в полученном наборе нечетное количество чисел, то медиана —это число, стоящее посередине; если в полученном наборе четное количество чисел, то медиана равна полусумме двух чисел, стоящих посередине.

Мера рассеивания (мера разброса) — числовая характеристика, показы­вающая, насколько близко к среднему значению группируются числа в наборе или значения случайной величины. Наиболее употребительные меры рассеива­ния — размах набора, средний модуль отклонения, дисперсия (средний квадрат отклонения) и стандартное отклонение (арифметический квадратный корень из дисперсии).

Наибольшее значение набора — число в наборе, которое не меньше, чем любое другое число этого набора.

Наименьшее значение набора — число в наборе, которое не больше, чем любое другое число этого набора.

Невозможное событие — событие, вероятность которого в данном опыте равна нулю. Невозможное событие противоположно достоверному.

Независимые события. Два события А и В называются независимыми, если вероятность их пересечения равна произведению их вероятностей:

Р(А∩В)=Р(А)-Р(В).

Часто независимость событий объясняется независимостью опытов, к ко­торым они относятся. Например, независимы два события, относящиеся к различным испытаниям Бернулли.

Независимые случайные величины. Если любые два события, одно из которых связано со случайной величиной X, а другое — со случайной величи­ной Y, независимы, то случайные величины Xи Yназываются независимыми.

Аналогично определяется произвольное количество независимых величин.

Важным примером независимых величин является число успехов в различ­ных независимых испытаниях Бернулли.

Для независимых случайных величин Xи Yверны следующие свойства:

1) Е(ХУ) = Е(Х)-Е(У);

2) D(X + Y)=D(X)+D(Y).

Несовместные события — два события, которые не могут наступить в од­ном и том же опыте вместе (одновременно). Примером несовместных событий являются противоположные события.

Номинальный вес изделия — вес изделия, который должен получиться со­гласно технологии производства. Вес изделия при массовом производстве — величина изменчивая, поэтому для каждого изделия вес может немного отли­чаться от номинального.

Объединение (сумма) событий. Объединением событий А и В называется событие, которое происходит в том и только в том случае, когда происходит хотя бы одно из событий А и В.

Орел — одна из сторон монеты (реверс). Другая сторона (аверс) называется решкой. Выпадение орла —одно из двух элементарных событий при бросании монеты.

Отклонение стандартное (среднее квадратичное) — мера рассеивания, ко­торая равна арифметическому квадратному корню из дисперсии случайной величины:

σ=

Пересечение (произведение) событий. Пересечением событий А и В на­зывается событие, которое происходит в том и только в том случае, когда наступают оба события А и В.

Перестановка — один из способов нумерации элементов некоторого множества. Если в множестве п элементов, то существует п! перестановок этих элементов.

Правило сложения вероятностей — правило, по которому вычисляется вероятность объединения событий. Для двух произвольных событий А и В верна формула

Р (АUВ)=Р(А)+Р(В)-Р(А∩В).

Если события А и В несовместны, то формула принимает более простой вид:

P(AUB)=P(A)+P(B).

Правило умножения вероятностей — правило, которое гласит, что

вероятность пересечения независимых событий равна произведению их вероятностей:

Р(А∩В) = Р(А)∙Р(В).

Правило умножения комбинаторное — правило, которое гласит, что число пар из двух предметов двух типов равно

т ∙n,

где т—число предметов первого типа, п—число предметов второго типа. Имеется в виду, что в паре на первом месте стоит предмет первого типа, на втором – предмет второго типа.

Аналогично вычисляется число упорядоченных наборов, состоящих из предметов трех, четырех и более типов.

Противоположное событие. Событием, противоположным событию А называется событие , состоящее в том, что событие А не наступило. Можно сказать иначе: событие наступает тогда и только тогда, когда не наступает событие А.

Равновозможные элементарные события — элементарные события, у которых одинаковые шансы на наступление. Примером может служить опыт, состоящий в бросании правильной игральной кости. В этом опыте шесть элементарных событий, и все они равновозможны.

Равновероятные события — события, вероятности которых равны.

Приме ром равновероятных событий могут служить равновозможные элементарные события. В опыте с бросанием игральной кости вероятность каждого из элементарных событий равна , поэтому все они равновероятны.

Размах набора — разность между наибольшим и наименьшим значением этого набора.

Распределение вероятностей — закон, по которому каждому значению слу­чайной величины в соответствие ставится вероятность того, что величина при­мет это значение. Распределение для конечной случайной величины можно задать таблицей, диаграммой или формулой.

Решка — одна из сторон монеты (аверс). Другая сторона (реверс) называется орлом. Выпадение решки — одно из двух элементарных событий при бросании монеты.

Серия испытаний Бернулли — случайный эксперимент, состоящий в по­следовательном проведении нескольких отдельных независимых испытаний Бернулли с одной и той же вероятностью успеха.

Систематическая ошибка — одна и та же ошибка, возникающая при любом измерении или наблюдении и связанная с настройкой прибора. Например, если весы не отрегулированы, то они все время могут показывать на 10 г больше, чем надо. Здесь 10 г — систематическая ошибка.

Если систематической ошибки нет, то все другие отклонения связаны со случайной изменчивостью и называются случайными ошибками измерения.

Случайная величина—величина, которая принимает те или иные значения в ходе случайного опыта под воздействием случая.

Случайная изменчивость — способность некоторой величины принимать различные значения по воле случая, т. е. под воздействием различных обстоя­тельств, которые нет возможности ни предвидеть, ни изменить.

Случайное событие—событие, которое может наступить в ходе некоторого опыта, а может не наступить. Наступит случайное событие или нет — дело случая.

Случайный выбор — см. выбор наудачу.

Случайный опыт (случайный эксперимент) — математическая абстрак­ция, описывающая реальный опыт, который может оканчиваться различны­ми случайными событиями. Под случайным опытом можно также понимать наблюдение за некоторым явлением природы или измерение некоторой ве­личины (длины, массы и т. п.). Иногда случайный опыт проводят намерен­но. Примером может служить любая игра или лотерея, спортивное состя­зание.

Социологическое обследование — сбор информации об обществе с помо­щью опроса специально отобранной группы населения (выборки). Примером социологического обследования может служить предварительный опрос изби­рателей, тестирование учащихся или абитуриентов, изучение спроса и предло­43жения товаров.

Сочетание. Любой набор к предметов, отобранных из набора, в котором п предметов, называется сочетанием из п по к.

Среднее набора чисел — среднее арифметическое чисел этого набора, т. е. их сумма, деленная на их количество.

Статистика — наука, посвященная методам систематизации, обработки и использования большого количества числовых данных. Такие данные назы­ваются статистическими. Важным примером статистических данных может служить численность групп населения страны, данные о производстве того или иного вида продукции, сведения о спросе и предложении какого-либо товара.

Теория вероятностей — раздел математики, изучающий вероятности собы­тий. Теория вероятностей разрабатывает методы, с помощью которых можно вычислить вероятности одних событий, зная вероятности других. Теория веро­ятностей изучает также случайные величины и их распределения.

Точность измерения. Под точностью измерения часто понимают допусти­мую ошибку, которую можно сделать при измерении. Например, измеряя рост человека, говорят об измерении с точностью до сантиметра.

Под точностью измерения также понимают разность между результатом измерения и истинным значением величины (длины, массы и т. п.).

Факториал. Факториалом натурального числа п называется произведение всех натуральных чисел, не превосходящих п. Факториал числа п обозначает­ся n!.

Таким образом, для натурального п факториал вычисляется по формуле

n!=1∙2∙3∙4∙…∙n

Факториал нуля по определению полагают равным единице: 0! = 1.

Частота. Пусть при проведении п случайных опытов событие А наступило

к раз. Частотой события А называется отношение .

Число сочетаний. Число различных сочетаний из п по к обозначается С^к и вычисляется по формуле =

Число успехов в серии испытаний Бернулли. Вероятность того, что в результате серии из п испытаний Бернулли наступит ровно к успехов, равна

P(S= k)=

где р и q — соответственно вероятности успеха и неудачи.

Численность (объем) выборки — количество чисел, людей, предметов в исследуемой выборке.

Элементарное событие — простейшее событие, которое наступает в ре­зультате случайного опыта. Элементарное событие нельзя разложить на более простые.

Любое событие опыта состоит из некоторых элементарных событий в том смысле, что является их объединением. Еще говорят, что элементарное событие может благоприятствовать некоторому событию.

Приложение 1

Задание 1. Классическое определение вероятности.

1. В отделе работают 7 мужчин и 3 женщины. В командировку отобраны 5 человек. Определить вероятность того, что среди них две женщины.

2. Из шести карточек с буквами И К С Т У Э наугад одну за другой выбирают четыре карточки и располагают в ряд в порядке появления. Какова вероятность того, что получится слово «СТУК»?

3. Совет директоров состоит из трех бухгалтеров и четырех менеджеров. Планируется создать подкомитет из его членов. Какова вероятность того, что все трое в подкомитете будут менеджеры.

4. На складе имеется 15 телевизоров, причем 10 из них изготовлены Симферопольским заводом «Фотон». Найти вероятность, что среди четырех выбранных наудачу телевизоров, нет изготовленных в Симферополе.

5. В папке 10 квитанций, три из которых заполнены неверно. Наудачу извлечены 6 квитанций. Найти вероятность того, что среди извлеченных – две квитанции заполнены неверно.

6. В группе 13 студентов, среди которых 5 отличников. По списку наудачу отобраны 8 студентов. Найти вероятность того, что среди них трое отличников.

7. В компьютерном классе 10 машин, 7 из которых подключены к сети Internet. Наудачу выбраны три машины. Найти вероятность того, что одна из них подключена к сети Internet.

8. Устройство содержит 7 элементов, из которых три изношены. При включении устройства включаются случайным образом три элемента. Найти вероятность того, что включенными окажутся два изношенных элемента.

9. В ящике содержится 10 деталей, из них 4 бракованные. Наудачу извлечены три детали. Найти вероятность того, что среди извлеченных только одна бракованная.

10. Набирая номер телефона абонент забыл три последние цифры и, помня лишь, что эти цифры разные набрал их наугад. Найти вероятность того, что набраны нужные цифры.

11. В чемпионате института по футболу участвуют 6 команд, 4 из которых представляют факультет экономики. Для жеребьевки декан пригласил трех капитанов команд, какова вероятность того, что все они с факультета экономики?

12. В отделе работают 7 мужчин и 3 женщины. В командировку отобраны 5 человек. Определить вероятность того, что среди них только одна женщина.

13. Совет директоров состоит из трех бухгалтеров и четырех менеджеров. Планируется создать подкомитет из его членов. Какова вероятность того, что среди трех членов подкомитета два бухгалтера.

14. На складе имеется 15 телевизоров, причем 10 из них изготовлены Симферопольским заводом «Фотон». Найти вероятность, что среди четырех выбранных наудачу телевизоров, два телевизора Симферопольского завода.

15. Устройство содержит 7 элементов, из которых три изношены. При включении устройства включаются случайным образом три элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.

16. В ящике содержится 10 деталей, из них 4 бракованные. Наудачу извлечены три детали. Найти вероятность того, что среди извлеченных нет бракованных.

17. Из шести карточек с буквами И К С Т У Э наугад одну за другой выбирают четыре карточки и располагают в ряд в порядке появления. Какова вероятность того, что получится слово «КУСТ»?

18. Из 30 вопросов, входящих в билеты зачета студент подготовил 26. Какова вероятность того, что взятый наудачу студентом билет, содержащий два вопроса, будет состоять из подготовленных им вопросов?

19. В папке 10 квитанций, три из которых заполнены неверно. Наудачу извлечены 6 квитанций. Найти вероятность того, что среди извлеченных нет неверно заполненных квитанций.

20. В компьютерном классе 10 машин, 7 из которых подключены к сети Internet. Наудачу выбраны три машины. Найти вероятность того, что все три подключены к сети Internet.

21. Декан пригласил на беседу двоих студентов, имеющих задолженности по высшей математике, через старосту группы. Староста забыл фамилии приглашенных, и отправил двоих из имеющихся пяти задолжников. Какова вероятность того, что это нужные декану студенты?

22. Среди 16 студентов группы, из которых семь девушки, разыгрывается 6 билетов, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билетов окажутся четыре девушки?

23. В отделе работают 6 мужчин и 4 женщины. В командировку отобраны 5 человек. Определить вероятность того, что среди них нет женщин.

24. Совет директоров состоит из трех бухгалтеров и четырех менеджеров. Планируется создать подкомитет из его членов. Какова вероятность того, что среди трех членов подкомитета два менеджера.

25. На складе имеется 15 телевизоров, причем 10 из них изготовлены Симферопольским заводом «Фотон». Найти вероятность, что среди четырех выбранных наудачу телевизоров, все телевизоры Симферопольского завода.

26. Устройство содержит 7 элементов, из которых три изношены. При включении устройства включаются случайным образом три элемента. Найти вероятность того, что включенными окажутся все изношенные элементы.

27. В ящике содержится 10 деталей, из них 4 бракованные. Наудачу извлечены три детали. Найти вероятность того, что среди извлеченных нет годных.

28. В чемпионате института по футболу участвуют 6 команд, 4 из которых представляют факультет экономики. Для жеребьевки декан пригласил трех капитанов команд, какова вероятность того, что двое из них с факультета экономики?

29. Из шести карточек с буквами И К С Т У Э наугад одну за другой выбирают четыре карточки и располагают в ряд в порядке появления. Какова вероятность того, что можно будет прочесть СИЭУ?

30. В папке 10 квитанций, три из которых заполнены неверно. Наудачу извлечены 6 квитанций. Найти вероятность того, что среди извлеченных только одна квитанция заполнена неверно.

Задание 2. Теоремы сложения и умножения вероятностей

1. В мешке смешаны нити, среди которых 80% белые, а остальные – красные. Определить вероятность того, что вынутые наудачу две нити окажутся одного цвета.

2. Рабочий обслуживает три станка. Вероятность того, что в течение смены его внимания потребует первый станок равна 0.3, второй – 0.35, третий – 0.15. Найти вероятность того, что в течение смены внимания рабочего потребуют какие-либо два станка.

3. Вероятность того, что пришедший в библиотеку студент закажет учебное пособие по теории вероятностей равна 0.05. Найти вероятность того, что среди троих первых студентов, пришедших в библиотеку, только один закажет учебное пособие по теории вероятностей.

4. Среди производимых рабочим деталей 6% брака. Какова вероятность того, что среди взятых на испытание четырех деталей хотя бы одна бракованная.

5. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов равна 0.4, второй – 0.7, третий – 0.3. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент услышит вызов радиста.

6. По цели стреляют два торпедных катера. Вероятность попадания в цель для первого катера равна 0.7, для второго – 0.85. Для поражения цели достаточно попадания в нее одной торпеды. Каждый катер делает по одному выстрелу. Определить вероятность того, что цель поражена.

7. Для сообщения об аварии установлены два независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство равна 0.7, второе – 0.9. Найти вероятность того, что при аварии сработает только одно устройство.

8. Деталь проходит три операции обработки. Вероятность того, что она окажется бракованной после первой операции равна 0.05, после второй – 0.07, после третьей – 0.1. Найти вероятность того, что после трех операций деталь окажется бракованной, предполагая, что появление брака на отдельных операциях – независимые события.

9. В механизм входят три детали. Работа механизма нарушается, если хотя бы одна деталь выйдет из строя. Вероятность выйти из строя для первой детали – 0.1, для второй – 0.15, для третьей – 0.05. Найти вероятность нормальной работы механизма.

10. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос равна 0.9, на второй – 0.6, на третий – 0.8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить по крайней мере на один вопрос.

11. Заводом послана автомашина за различными материалами на четыре базы. Вероятность наличия нужного материала на первой базе равна 0.7, на второй – 0.9, на третьей – 0.75, на четвертой – 0.8. Найти вероятность того, что хотя бы на одной базе не окажется нужного материала.

12. Из партии деталей контролер отбирает стандартные. Вероятность того, что наудачу взятая деталь стандартная, равна 0.85. Найти вероятность того, что из трех проверенных деталей только две будут стандартные.

13. В первом ящике 1 белый, 3 красных и 1 синий шар, во втором 3 белых, 2 красных и 5 синих шаров. Из каждого ящика вынули по шару. Какова вероятность того, что среди вынутых шаров хотя бы один красный шар?

14. Вероятности того, что нужная сборщику деталь содержится в первом, втором, третьем ящике соответственно равны 0.7, 0.5, 0.9. Найти вероятность того, что деталь содержится хотя бы в одном ящике.

15. Студент записан в три библиотеки, в которых он разыскивает нужную ему книгу по комбинаторике. Вероятность найти книгу в первой библиотеке равна 0.2, во второй – 0.7, в третьей – 0.5. Найти вероятность того, что книгу можно найти хотя бы в одной библиотеке.

16. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него будут сброшены три бомбы с вероятностями попадания соответственно равными 0.7, 0.2, 0.85.

17. В одном ящике 3 белых и 7 красных шаров, в другом 6 белых и 4 красных. Из каждого ящика наудачу извлекают по одному шару. Найти вероятность того, что хотя бы из одного ящика будет извлечен белый шар.

18. Вероятность того, что в течение одной смены станок выйдет из строя равна 0.1. Какова вероятность того, что не произойдет ни одной неполадки за три смены?

19. В первом ящике 1 белый, 3 красных и 1 синий шар, во втором 3 белых, 2 красных и 5 синих шаров. Из каждого ящика вынули по шару. Какова вероятность того, что среди вынутых шаров нет синих?

20. В мешке смешаны нити, среди которых 80% белые, а остальные – красные. Определить вероятность того, что вынутые наудачу две нити окажутся разных цветов.

21. Рабочий обслуживает три станка. Вероятность того, что в течение смены его внимания потребует первый станок равна 0.3, второй – 0.35, третий – 0.15. Найти вероятность того, что в течение смены внимания рабочего потребует хотя бы один станок.

22. Для сообщения об аварии установлены два независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство равна 0.7, второе – 0.9. Найти вероятность того, что при аварии сработает хотя бы одно устройство.

23. В механизм входят три детали. Работа механизма нарушается, если хотя бы одна деталь выйдет из строя. Вероятность выйти из строя для первой детали – 0.1, для второй – 0.15, для третьей – 0.05. Найти вероятность того, что работа механизма будет нарушена.

24. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на первый вопрос равна 0.9, на второй – 0.6, на третий – 0.8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить по крайней мере на два вопроса.

25. Заводом послана автомашина за различными материалами на четыре базы. Вероятность наличия нужного материала на первой базе равна 0.7, на второй – 0.9, на третьей – 0.75, на четвертой – 0.8. Найти вероятность того, что только на одной базе не окажется нужного материала.

26. Из партии деталей контролер отбирает стандартные. Вероятность того, что наудачу взятая деталь стандартная, равна 0.85. Найти вероятность того, что из трех проверенных деталей хотя бы одна нестандартная.

27. Вероятности того, что нужная сборщику деталь содержится в первом, втором, третьем ящике соответственно равны 0.7, 0.5, 0.9. Найти вероятность того, что деталь содержится по крайней мере в двух ящиках.

28. Студент записан в три библиотеки, в которых он разыскивает нужную ему книгу по комбинаторике. Вероятность найти книгу в первой библиотеке равна 0.2, во второй – 0.7, в третьей – 0.5. Найти вероятность того, что книгу можно найти по крайней мере в двух библиотеках.

29. В одном ящике 3 белых и 7 красных шаров, в другом 6 белых и 4 красных. Из каждого ящика наудачу извлекают по одному шару. Найти вероятность того, что оба извлеченных шара красные.

30. В первом ящике 1 белый, 3 красных и 1 синий шар, во втором 3 белых, 2 красных и 5 синих шаров. Из каждого ящика вынули по шару. Какова вероятность того, что среди вынутых шаров нет белых шаров?

Задание 3. Формула полной вероятности. Формула Бейеса

1. Имеется два одинаковых ящика с шарами. В первом ящике 4 белых и 6 красных шаров, во втором 5 белых и 10 красных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется белым?

2. Предприятие имеет три источника поставки комплектующих – фирмы А, В, С. на долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, В – 5% и С – 6%. Какова вероятность того, что наугад взятая деталь стандартная?

3. В студенческой группе 20 человек. из них 4 человека сдали экзамен по высшей математике на «отлично», 11 на «хорошо» и 5 на «удовлетворительно». Вероятность решить предложенную задачу для отличника составляет 0.9, для хорошиста 0.8, для троечника 0.7. Определить вероятность того, что наудачу выбранный студент не решит задачу.

4. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника 0.9, для велосипедиста 0.8 и для бегуна 0.75. Найти вероятность того, что наудачу выбранный спортсмен не выполнит норму.

5. В первой урне 3 белых и 7 черных шаров, во второй – 6 белых и 4 черных шаров. Из второй урны в первую переложили один шар, а затем из первой урны вынули наугад один шар. Какова вероятность того, что вынутый шар ранее находился во второй урне, если известно, что он белый.

6. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы второго курса 4 студента, из второй группы 6 студентов, из третьей группы 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равны 0.6, 0.9, 0.5. Найти вероятность того, что наудачу выбранный студент не попадет в сборную.

7. В первом ящике 20 деталей, из них 15 стандартные. Во втором ящике 25 деталей, из них 20 стандартные. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика – стандартная.

8. Сборщик получил 5 коробок деталей изготовленных заводом №1 и 4 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна равна 0.9, а завода №2 – 0.72. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.

9. В студенческой группе 25 человек. из них 5 человека сдали экзамен по высшей математике на «отлично», 12 на «хорошо» и 8 на «удовлетворительно». Вероятность решить предложенную задачу для отличника составляет 0.9, для хорошиста 0.8, для троечника 0.7. Определить вероятность того, что наудачу выбранный студент решит задачу.

10. На заводе изготовляют комплектующие детали. Первая машина производит 25% всех изделий, вторая 35%, третья 40%. Брак составляет соответственно 5%, 4% и 10%. Какова вероятность того, что случайно выбранная деталь имеет дефект?

11. В группе спортсменов 15 лыжников, 9 велосипедистов и 6 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника 0.95, для велосипедиста 0.9 и для бегуна 0.7. Найти вероятность того, что наудачу выбранный спортсмен выполнит норму.

12. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы второго курса 5 студентов, из второй группы 4 студента, из третьей группы 6 студентов. Вероятности того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равны 0.6, 0.9, 0.7. Найти вероятность того, что наудачу выбранный студент попадет в сборную.

13. Предприятие имеет три источника поставки комплектующих – фирмы А, В, С. на долю фирмы А приходится 45% общего объема поставок, В – 25% и С – 30%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, В – 8% и С – 7%. Какова вероятность того, что взятая наугад и оказавшаяся бракованной деталь получена от фирмы А?

14. В первом ящике 30 деталей, из них 20 стандартные. Во втором ящике 20 деталей, из них 15 стандартные. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика – бракованная.

15. Имеется два одинаковых ящика с шарами. В первом ящике 10 белых и 5 черных шаров, во втором 3 белых и 7 черных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется белым?

16. Сборщик получил 4 коробки деталей изготовленных заводом №1 и 6 коробок деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна равна 0.7, а завода №2 – 0.8. Сборщик наудачу извлек деталь из наудачу взятой коробки. Извлечена стандартная деталь. Определить вероятность того, что она изготовлена заводом №2.

17. На заводе изготовляют комплектующие детали. Первая машина производит 30% всех изделий, вторая 50%, третья 20%. Брак составляет соответственно 7%, 6% и 10%. Какова вероятность того, что случайно выбранная деталь стандартная?

18. Предприятие имеет три источника поставки комплектующих – фирмы А, В, С. на долю фирмы А приходится 40% общего объема поставок, В – 25% и С – 35%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, В – 4% и С – 6%. Какова вероятность того, что наугад взятая деталь бракованная?

19. В первой урне 5 белых и 15 черных шаров, во второй – 13 белых и 7 черных шаров. Из второй урны в первую переложили один шар, а затем из первой урны вынули наугад один шар. Определить вероятность того, что вынутый шар – белый.

20. В студенческой группе 20 человек. из них 4 человека сдали экзамен по высшей математике на «отлично», 11 на «хорошо» и 5 на «удовлетворительно». Вероятность решить предложенную задачу для отличника составляет 0.9, для хорошиста 0.8, для троечника 0.7. Наудачу выбранный студент решил задачу. Определить вероятность того, что это отличник.

21. Имеется два одинаковых ящика с шарами. В первом ящике 14 белых и 6 красных шаров, во втором 15 белых и 10 красных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется красным?

22. В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника 0.9, для велосипедиста 0.8 и для бегуна 0.75. Наудачу выбранный спортсмен выполнил норму. Определить вероятность того, что это велосипедист.

23. На заводе изготовляют комплектующие детали. Первая машина производит 25% всех изделий, вторая 35%, третья 40%. Брак составляет соответственно 6%, 4% и 9%. Случайно выбранная деталь оказалась бракованной. Какова вероятность того, что она была произведена первой машиной?

24. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы второго курса 4 студента, из второй группы 6 студентов, из третьей группы 5 студентов. Вероятность того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равна 0.6, 0.8, 0.5. Наудачу выбранный студент попал в сборную. Определить вероятность того, что это студент из первой группы.

25. Сборщик получил 6 коробок деталей изготовленных заводом №1 и 4 коробки деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна равна 0.8, а завода №2 – 0.75. Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена бракованная деталь.

26. На заводе изготовляют комплектующие детали. Первая машина производит 40% всех изделий, вторая 35%, третья 25%. Брак составляет соответственно 5%, 4% и 9%. Случайно выбранная деталь оказалась стандартной. Какова вероятность того, что она была произведена третьей машиной?

27. Имеется два одинаковых ящика с шарами. В первом ящике 10 белых и 15 черных шаров, во втором 13 белых и 17 черных. Наудачу выбирают один ящик и извлекают из него шар. Какова вероятность того, что извлеченный шар окажется черным?

28. Предприятие имеет три источника поставки комплектующих – фирмы А, В, С. на долю фирмы А приходится 35% общего объема поставок, В – 25% и С – 40%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, В – 5% и С – 7%. Какова вероятность того, что взятая наугад и оказавшаяся стандартной деталь получена от фирмы В?

29. В первой урне 15 белых и 5 черных шаров, во второй – 14 белых и 6 черных шаров. Из второй урны в первую переложили один шар, а затем из первой урны вынули наугад один шар. Определить вероятность того, что вынутый шар – черный.

30. Сборщик получил 14 коробок деталей изготовленных заводом №1 и 16 коробок деталей, изготовленных заводом №2. Вероятность того, что деталь завода №1 стандартна равна 0.75, а завода №2 – 0.8. Сборщик наудачу извлек деталь из наудачу взятой коробки. Извлечена нестандартная деталь. Определить вероятность того, что она изготовлена заводом №1.

Задание 4. Повторные независимые испытания по схеме Бернулли

1. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди 600 взятых наугад изделий 25 бракованных.

2. Вероятность получения хорошего результата при проведении маркетинговых исследований равна 0.7. Найти вероятность наивероятнейшего числа удачных исследований, если общее их количество равно 8.

3. Среди семян ржи имеется 0.2% семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить не более 3 семян сорняков?

4. Вероятность появления успеха в каждом испытании равна 0.4. Найти вероятность того, что при 550 испытаниях успех наступит не менее 210 и не более 240 раз.

5. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна 0.01. Телефонная станция обслуживает 900 абонентов. Какова вероятность того, что в течение часа позвонят пять абонентов?

6. В первые классы должно быть принято 400 детей. Определить вероятность того, что среди них окажется 200 девочек, если вероятность рождения мальчика равна 0.515.

7. Вероятность рождения мальчика равна 0.515, а девочки – 0.485. в некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.

8. Имеется группа, состоящая из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день равна 1/365.

9. Вероятность поражения мишени при одном выстреле равна 0.8. Найти вероятность того, что при 300 выстрелах мишень будет поражена не менее 230 раз.

10. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Какова вероятность того, что из четырех вынутых шаров окажется два черных?

11. Известно, что 5% продукции, поставляемой заводом на торговую базу, не удовлетворяет всем требованиям стандарта. На базу поступило 9 изделий. Найти наивероятнейшее число изделий, удовлетворяющих требованиям стандарта, и вычислить вероятность того, что среди поступивших окажется наивероятнейшее число годных изделий.

12. Найти вероятность того, что событие А наступит ровно 75 раз в 400 испытаниях, если вероятность события А в каждом испытании равна 0.2.

13. Вероятность изготовления нестандартной детали на станке-автомате равна 0.003. Найти вероятность того, что среди 1000 деталей окажется 4 нестандартных.

14. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди семи взятых наугад изделий два бракованных.

15. Вероятность выхода за границы поля допуска при обработке деталей на токарном станке равна 0.07. Определить вероятность того, что из шести наудачу отобранных в течение смены деталей у одной размеры диаметра не соответствуют заданному допуску.

16. Монету подбрасывают 6 раз. Какова вероятность того что она упадет гербом вверх не менее пяти раз?

17. Вероятность появления события А равна 0.6. Какова вероятность того, что при 800 испытаниях событие А появится не более 470 раз?

18. Вероятность появления успеха в каждом испытании равна 0.3. Найти вероятность того, что при 400 испытаниях успех наступит 110 раз.

19. В первые классы должно быть принято 200 детей. Определить вероятность того, что среди них окажется 100 девочек, если вероятность рождения мальчика равна 0.515.

20. Вероятность рождения мальчика равна 0.515, а девочки – 0.485. в некоторой семье шестеро детей. Найти вероятность того, что среди них нет девочек.

21. Вероятность появления события А равна 0.4. Какова вероятность того, что при 600 испытаниях событие А появится не менее 230 раз?

22. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Какова вероятность того, что из четырех вынутых шаров окажется два белых?

23. Вероятность получения хорошего результата при проведении маркетинговых исследований равна 0.6. Найти наивероятнейшее число удачных исследований, если общее их количество равно 7 и вероятность этого числа исследований.

24. Вероятность попадания стрелком в цель равна 0.85. Сделано 7 выстрелов. Определить вероятность наивероятнейшего числа промахов.

25. Найти вероятность того, что событие А наступит не менее 75 и не более 90 раз в 400 испытаниях, если вероятность события А в каждом испытании равна 0.2.

26. Вероятность изготовления нестандартной детали на станке-автомате равна 0.003. Найти вероятность того, что среди 1000 деталей окажется не более 2 нестандартных.

27. Вероятность появления события А равна 0.6. Какова вероятность того, что при 8 испытаниях событие А появится не более трех раз?

28. Среди семян ржи имеется 0.4% семян сорняков. Какова вероятность при случайном отборе 5000 семян обнаружить 5 семян сорняков?

29. Вероятность поражения мишени при одном выстреле равна 0.9. Найти вероятность того, что при 200 выстрелах мишень будет поражена ровно 175 раз.

30. Четыре элемента вычислительного устройства работают независимо друг от друга. Вероятность безотказной работы для каждого элемента равна 0.75. Найти вероятность того, что ни один элемент не будет работать безотказно.

Задание 5. Дискретные случайные величины и их числовые характеристики

Закон распределения дискретной случайной величины задан в виде таблицы.

Найти:

1) математическое ожидание ;

2) дисперсию ;

3) среднее квадратическое отклонение ;

4) начальные и центральные моменты первого, второго и третьего порядков.

Построить многоугольник распределения.

1.		20	25	30	35	40		2.		10	20	30	40	50
		0.2	0.3	0.2	0.1	0.2				0.1	0.3	0.2	0.1	0.3
3.		15	25	35	45	55		4.		10	30	50	70	90
		0.2	0.3	0.1	0.2	0.2				0.3	0.1	0.2	0.1	0.3
5.		20	30	40	50	60		6.		15	35	55	75	95
		0.1	0.4	0.1	0.3	0.1				0.1	0.3	0.1	0.4	0.1
7.		10	35	50	75	90		8.		5	25	50	75	80
		0.2	0.3	0.1	0.3	0.1				0.1	0.4	0.1	0.3	0.1
9.		40	50	60	70	80		10.		35	50	75	80	90
		0.1	0.2	0.1	0.5	0.1				0.1	0.5	0.1	0.2	0.1
11.		11	22	33	44	55		12.		55	66	77	88	99
		0.2	0.4	0.1	0.2	0.1				0.1	0.2	0.1	0.4	0.2
13.		3	23	33	43	53		14.		6	16	26	46	66
		0.1	0.1	0.5	0.1	0.2				0.2	0.1	0.5	0.1	0.1
15.		17	27	47	57	77		16.		4	14	44	64	94
		0.3	0.1	0.2	0.1	0.3				0.2	0.3	0.2	0.1	0.2
17.		9	29	59	69	99		18.		7	47	57	67	77
		0.1	0.3	0.2	0.1	0.3				0.2	0.3	0.1	0.2	0.2
19.		8	18	58	68	88		20.		22	62	72	82	92
		0.3	0.1	0.2	0.1	0.3				0.1	0.4	0.1	0.3	0.1
21.		10	40	55	60	90		22.		5	12	19	26	33
		0.1	0.3	0.1	0.4	0.1				0.2	0.3	0.1	0.3	0.1
23.		27	53	61	82	95		24.		36	41	55	77	89
		0.1	0.4	0.1	0.3	0.1				0.1	0.5	0.1	0.2	0.1
25.		33	43	67	81	99		26.		27	77	85	91	98
		0.1	0.5	0.1	0.2	0.1				0.2	0.4	0.1	0.2	0.1
27.		12	22	52	82	92		28.		13	23	63	73	83
		0.1	0.2	0.1	0.4	0.2				0.1	0.1	0.5	0.1	0.2
29.		11	21	51	61	91		30.		25	35	55	75	80
		0.2	0.1	0.5	0.1	0.1				0.3	0.1	0.2	0.1	0.3

Задание 6. Система двух случайных величин

Распределение вероятностей дискретной двумерной случайной величины задано таблицей.

Найти: 1) законы распределения составляющих и ;

2) математические ожидания и дисперсии составляющих;

3) коэффициент корреляции;

1.		4	9	12	2.		7		12		16
	6	0.16	0.14	0.35		6	0.13		0.15		0.18
	7	0.20	0.10	0.05		8	0.26		0.17		0.11
3.		5	10	15	4.		8		13		17
	3	0.19	0.11	0.25		10	0.18		0.21		0.04
	4	0.15	0.25	0.05		12	0.27		0.17		0.13
5.		3	11	14	6.		9		12		18
	7	0.18	0.02	0.3		11	0.19		0.34		0.07
	8	0.21	0.10	0.19		12	0.17		0.18		0.05
7.		2	8	17	8.		10		13		19
	5	0.22	0.18	0.03		12	0.21		0.07		0.15
	6	0.12	0.32	0.13		13	0.06		0.32		0.19
9.		3	5	12	10.			11		17	20
	2	0.17	0.06	0.12		13		0.06		0.31	0.07
	4	0.24	0.15	0.26		15		0.18		0.17	0.21
11.		4	7	15	12.			12		14	21
	3	0.14	0.27	0.08		14		0.04		0.22	0.09
	5	0.23	0.04	0.24		15		0.29		0.08	0.28
13.		5	10	14	14.			13		18	24
	4	0.13	0.21	0.07		15		0.15		0.03	0.16
	6	0.08	0.29	0.22		17		0.12		0.31	0.23
15.		6	11	15	16.			11		18	22
	5	0.11	0.22	0.08		16		0.26		0.11	0.07
	7	0.21	0.36	0.02		17		0.04		0.39	0.13
17.		21	25	29	18.			12		22	32
	17	0.03	0.31	0.08		20		0.04		0.24	0.06
	18	0.14	0.28	0.16		21		0.27		0.11	0.28
19.		19	24	28	20.			17		27	37
	17	0.12	0.03	0.14		21		0.08		0.25	0.11
	19	0.21	0.27	0.23		22		0.23		0.06	0.27
21.		17	20	27	22.			31		35	39
	18	0.20	0.03	0.24		25		0.15		0.20	0.25
	19	0.11	0.29	0.13		26		0.16		0.15	0.09
23.		18	21	26	24.			29		36	41
	18	0.21	0.04	0.13		26		0.06		0.23	0.09
	20	0.15	0.30	0.17		27		0.27		0.13	0.22
25.		15	23	24	26.			30		37	43
	19	0.16	0.27	0.14		26		0.14		0.05	0.16
	21	0.03	0.32	0.08		28		0.21		0.31	0.13
27.		15	20	25	28.			45		51	56
	20	0.23	0.06	0.17		29		0.17		0.08	0.26
	22	0.12	0.16	0.26		30		0.12		0.26	0.11
29.		11	21	31	30.			19		24	29
	21	0.05	0.38	0.07		31		0.06		0.21	0.04
	23	0.18	0.13	0.19		32		0.29		0.09	0.31

Задание 7. Непрерывная случайная величина

Непрерывная случайная величина задана интегральной функцией.

Найти: а) дифференциальную функцию и построить ее график;

б) вероятность того, что в результате испытания примет значение, принадлежащее интервалу ;

в) математическое ожидание и среднее квадратическое отклонение .

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.
17.	18.
19.	20.
21.	22.
23.	24.
25.	26.
27.	28.
29.	30.

Задание 8. Функция двух случайных аргументов.

Даны законы распределения независимых случайных величин и . Найти закон распределения случайной величины .

1.		1	3	5		12	13	15
		0.1	0.7	0.2		0.5	0.1	0.4
2.		2	4	6		11	12	14
		0.6	0.1	0.3		0.2	0.5	0.3
3.		1	3	6		10	12	13
		0.2	0.7	0.1		0.6	0.1	0.3
4.		1	2	5		13	17	19
		0.5	0.1	0.4		0.1	0.1	0.8
5.		3	4	7		13	16	18
		0.1	0.7	0.2		0.4	0.1	0.5
6.		4	6	8		10	18	20
		0.2	0.6	0.2		0.6	0.3	0.1
7.		5	7	9		19	21	23
		0.4	0.2	0.4		0.2	0.6	0.2
8.		5	6	8		18	20	21
		0.3	0.4	0.3		0.1	0.8	0.1
9.		3	5	7		17	19	21
		0.4	0.1	0.5		0.1	0.7	0.2
10.		2	4	8		21	25	27
		0.1	0.2	0.7		0.6	0.3	0.1
11.		0	1	3		25	27	28
		0.1	0.6	0.3		0.8	0.1	0.1
12.		1	2	5		0	3	4
		0.7	0.1	0.2		0.1	0.3	0.6
13.		0	2	4		5	7	10
		0.2	0.6	0.2		0.2	0.3	0.5
14.		1	7	9		0	2	10
		0.1	0.4	0.5		0.7	0.1	0.2
15.		0	10	20		4	14	34
		0.2	0.6	0.2		0.1	0.7	0.2
16.		9	10	11		0	1	3
		0.3	0.1	0.6		0.2	0.7	0.1
17.		0	3	5		9	11	16
		0.1	0.2	0.7		0.1	0.6	0.3
18.		7	9	10		5	6	9
		0.2	0.5	0.3		0.4	0.1	0.5
19.		1	2	8		0	6	13
		0.5	0.1	0.4		0.3	0.6	0.1
20.		0	8	10		8	10	20
		0.3	0.1	0.6		0.1	0.8	0.1
21.		10	11	15		3	7	12
		0.5	0.1	0.4		0.1	0.8	0.1
22.		12	13	20		5	12	17
		0.6	0.3	0.1		0.2	0.3	0.5
23.		15	16	19		6	9	13
		0.7	0.2	0.1		0.4	0.2	0.4
24.		14	17	18		3	4	8
		0.1	0.8	0.1		0.2	0.6	0.2
25.		11	13	15		6	8	12
		0.4	0.5	0.1		0.6	0.1	0.3
26.		17	18	20		8	10	13
		0.3	0.1	0.6		0.5	0.2	0.3
27.		1	9	10		3	4	13
		0.2	0.5	0.3		0.4	0.1	0.5
28.		0	5	12		7	14	26
		0.1	0.7	0.2		0.3	0.6	0.1
29.		12	14	16		0	2	6
		0.6	0.1	0.3		0.2	0.7	0.1
30.		0	7	9		12	14	23
		0.5	0.2	0.3		0.1	0.6	0.3

Задание 9. Математическая статистика

По данному статистическому распределению выборки, извлеченной из генеральной совокупности нормально распределенного признака .

Построить полигон относительных частот.

Найти: 1) эмпирическую функцию распределения и построить ее график;

2) несмещенные оценки генеральной средней и генеральной дисперсии ;

3) моду , медиану и размах варьирования ;

4) доверительный интервал для оценки с надежностью математического ожидания , если известно генеральное среднее квадратическое отклонение .

Приложение 2