3.Теорема Ролля с доказательством.

Если функция y=f(x)-непрерывна на отрезке ab, дифференцируема во всех внутренних точках на ab, и f(a)=f(b), то существует хотябы одна точка c из интервала ab, такая, что f’(c)=0.

Док-во: Т.к. функция непрерывна на отрезке ab, то она достигает на этом отрезке своего наименьшего (m) и наибольшего (M) значения. Возможны 2 случая:

1) m=M, тогда функция f(x)-постоянна на ab и производная равна 0 на всем отрезке.

2) m≠M, пусть f(xM)=M, a f(xm)=m, т.к. f(a)=f(b), то f(xM)>f(xm), тогда либо xm, либо xM лежит внутри отрезка ab. Эту точку обозначим через с.

Вопрос №16

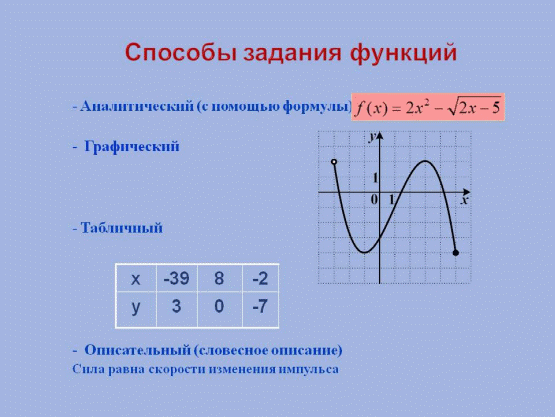
1.2. Функция, способы её задания, простейшие свойства

Основные обозначения:

N – натуральные числа,

Q – рациональные(дробные),

Z – целые числа,

R – действительные числа;

Вопрос 17

ВОПРОС №18

ВОПРОС №19

Вопрос №20