
- •Передмова
- •Критерії оцінювання
- •Завдання 1 на тему: «Прийняття рішень в умовах невизначеності. Методи оцінки ризику для прийняття рішень»
- •Хід роботи
- •Завдання до проведення роботи 1
- •Завдання 2 на тему: «Програмно-цільове управління та управлінські рішення. Моделі оптимізації господарської діяльності підприємства» (симплексний метод)
- •Нормативи витрат ресурсів і прибуток на ват «Меблева фабриці «Либідь» у 2009 р.
- •Хід роботи
- •Розрахунок дефіцитності ресурсів
- •Звіт з обмеження та міцності
- •Завдання до виконання роботи 2
- •Вихідні дані задачі
- •Завдання 3 на тему: «Прогнозування податкових надходжень»
- •Проміжні результати розрахунків
- •Результати розрахунків теоретичних значень податкових надходжень та їх залишків
- •Регресійний аналіз податкових надходжень
- •Завдання до виконання роботи 3
- •Мобілізовано податку з доходів фізичних осіб* до бюджету,
- •Рекомендована літературА
Проміжні результати розрахунків
n |
Y |
t |
Yt |
y2 |
t2 |
1 |
5,5 |
1 |
5,5 |
1 |
30,25 |
2 |
6,0 |
2 |
12,0 |
4 |
36,00 |
3 |
6,0 |
3 |
18,0 |
9 |
36,00 |
4 |
6,5 |
4 |
26,0 |
16 |
42,25 |
5 |
7,0 |
5 |
35,0 |
25 |
49,00 |
6 |
7,5 |
6 |
45,0 |
36 |
56,25 |
7 |
7,5 |
7 |
52,5 |
49 |
56,25 |
8 |
8,0 |
8 |
64,0 |
64 |
64,00 |
9 |
8,0 |
9 |
72,0 |
81 |
64,00 |
10 |
8,5 |
10 |
85,0 |
100 |
72,25 |
|
70,5 |
55 |
415,0 |
385 |
506,25 |
Розрахуємо оцінки параметрів моделі:
![]() =5,5;
=5,5;
![]() =7,05.
=7,05.
 =
=![]() .
.
![]() =
=![]() =
=![]() =5,233.
=5,233.
Отже,
побудована модель має вигляд:
![]() .
.
Це означає, що якщо збільшити часовий проміжок на одну одиницю, то Y в середньому буде збільшуватись на 0,33 одиниці.
4. Розрахувати вектор залишків та його дисперсію.
Таблиця 3.3
Результати розрахунків теоретичних значень податкових надходжень та їх залишків
|
|
|
|
|
1 |
5,5 |
5,564 |
-0,064 |
0,004 |
2 |
6,0 |
5,894 |
0,1060 |
0,011 |
3 |
6,0 |
6,224 |
-0,224 |
0,050 |
4 |
6,5 |
6,555 |
-0,054 |
0,003 |
5 |
7,0 |
6,885 |
0,115 |
0,013 |
6 |
7,5 |
7,215 |
0,285 |
0,081 |
7 |
7,5 |
7,543 |
-0,045 |
0,002 |
8 |
8,0 |
7,876 |
0,124 |
0,015 |
9 |
8,0 |
8,206 |
-0,206 |
0,042 |
10 |
8,5 |
8,536 |
-0,036 |
0,001 |
|
|
|
0 |
0,224 |
Отже,
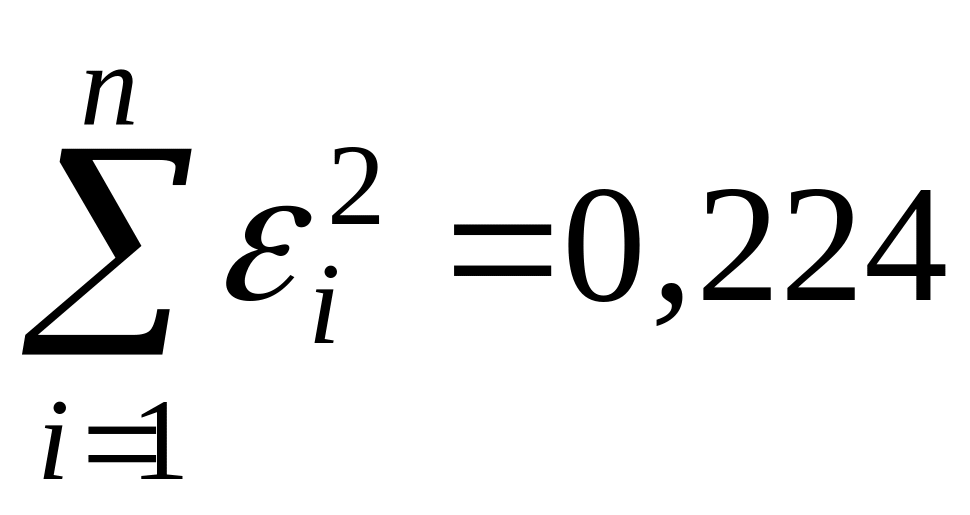 .
.
Розрахувати стандартну помилку залишків:
 .
.
95 %-тні довірчі інтервали для b1 : b1 b1= 0,33 0,018; 0,312 b1 0,348.
Для прийняття рішення про значимість розрахованої оцінки розрахуємо критерій Стьюдента:
![]() .
.
Критичне значення t-критерію при (n-2)=8 та =0,05 дорівнює 2,9. Оскільки воно набагато менше за розраховане, то нульова гіпотеза відхиляється, а отже, оцінка є значимою.
Індивідуальний
довірчий інтервал для
![]() буде дорівнювати:
буде дорівнювати:
![]() ,
,
3,74 b0 7,424.
Оскільки з інформаційної точки зору вільний член не становить особливого інтересу, то формально нема особливого сенсу у цих обрахунках. Разом з тим цікаво отримати відповідь на питання про значимість цієї оцінки. Для цього розрахуємо відповідний критерій Стьюдента і порівняємо його з критичним для n – 2 = 8 ступенів свободи та =0,05 рівня значимості.
 .
.
5. Розрахувати критерії адекватності:
а) коефіцієнт детермінації
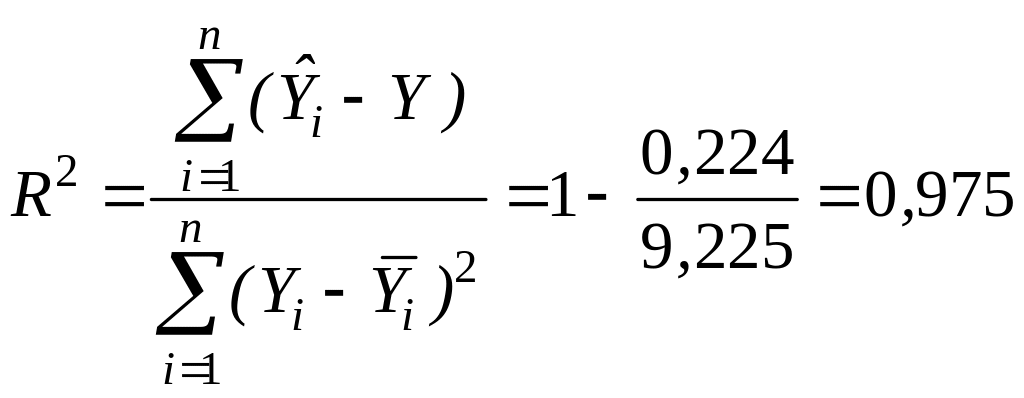 або
97,5% .
або
97,5% .
Це означає, що варіація податкових надходжень на 97,5 % залежить від часового фактора
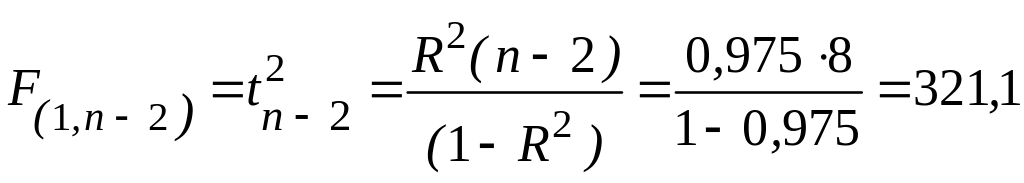 ,
Fтабл=3,4.
,
Fтабл=3,4.
Так як Fрозр. > Fтабл , то модель побудована якісно і може бути використана для прогнозу.
6. Розрахувати прогноз для точки t0 =10+N=10+11=21 .
![]() .
.
У середовищі Excel викликаємо процедуру регресійного аналізу:
Сервис>Анализ данных > Регрессия. Результати використання процедури регресійного аналізу наведені в табл. 3.4 і рис. 3.2.
Таблиця 3.4
