Лекция № 9-10 Содержание
1. Разомкнутые системы управления электроприводом.
1 Механические переходные процессы в разомкнутой системе электропривода.
Электромеханические аппараты и устройства управления.
Схемы управления ЭД постоянного тока.
. Пуск электродвигателя постоянного тока.
Схема торможения электродвигателя.
Схемы управления асинхронным короткозамкнутым двигателем (пуск и торможение).
Устройства плавного пуска, ДПТ и асинхронного короткозамкнутого двигателя.
Разомкнутые системы управления электроприводом
Механические переходные процессы в разомкнутых электроприводах
В простейших электромеханических системах привода обычно пренебрегают электрическими переходными процессами, считая, что изменение тока в цепях ЭД происходит гораздо быстрее, чем изменение скорости. При абсолютно жестких механических передачах движение привода описывается дифференциальным уравнением
M(w) - вращающий момент двигателя;
Mc(w) - момент cопротивления механизма;
I -момент инерции;
Mg(w) - динамический момент;
w - угловая скорость.
Рассмотрим случай, наиболее простой, когда Мg - линейная функция скорости, а момент сопротивления не зависит от скорости, Для привода имеющего линейную механическую характеристику момент равен
М(w)= (w0 -w)
- жёсткость механической характеристики двигателя.
Подставляя это выражение в (1) и деля всё , получим
где TM - электромеханическая постоянная времени.
Структурная схема простейшей электромеханической системы привода приведена на рисунке 1.
Рисунок 1 - Структурная схема привода, имеющего линейную
механическую характеристику
Привод представлен инерциальным звеном первого порядка (апериодичным звеном) с двумя внешними воздействиями: управляющим воздействием, или заданием скорости w0 и возмущением по моменту Мс / . Поскольку уравнение (2) и структурная схема содержат только механические параметры, то они образуют электромеханическую модель электропривода.
В установившемся режиме
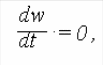
угловая скорость w=wуст для этого случая получим
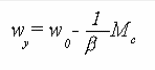
и тогда из (2), получим
Решение уравнения (3) при начальных условиях w(0)= wнач
w(t)=wy + ( wнач.- wy ) exp(-t/TM ) , (4)
если wнач=0, то w(t)=wy (1-exp( -t/TM ) (5)
График изменения скорости в переходном процессе при разгоне привода от начальной скорости до установившегося значения имеет вид (1) (смотри рисунок 2).
Рисунок 2 - Механические переходные процессы
в системе разомкнутого привода
Используя зависимость (4) можно определить изменение скорости привода при изменении момента сопротивления.
Например, от скорости
wy1=w0 - Mc1 / до скорости wy2=w0 - Mc2 /если Мс2>Мс1 то wy2<wy1 , в
результате, из (4)
w(t)=wy2+(wy1 - wy2 ) exp(-t / TM )
Кривая 2 на рисунке 2 показывает, как уменьшается скорость привода при увеличении нагрузки. Электромеханическая постоянная времени TM определяет темп механических переходных процессов. При t=TM скорость привода w=0.632 wy. Это соотношение часто принимают за определение электромеханической постоянной времени.
Также как и для постоянной времени нагрева, если провести касательную к графику w(t) до пересечения с установившимся уровнем скорости из точки w(0), то абсцисса точки пересечения будет ТМ. Отсюда вытекает другое определение ТМ, как времени разгона электропривода до установившейся скорости при постоянном ускорении, равном начальному.
Время переходного процесса при изменении скорости от w1 до w2 можно найти из уравнения привода (1).
Для вычисления этого интеграла необходимо знать зависимости движущего момента и момента сопротивления от скорости. В простейшем случае, если принять I - момент инерции постоянным (I=const) , M=const и Mc=const , тогда время переходного процесса tnn будет определяться уравнением 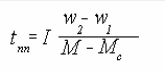(7).
(7)
Если w1=0 ,w2=wном , т.е. осуществляется пуск двигателя, тогда время пуска tnn будет равным (8).
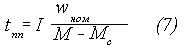
При торможении привода момент движения меняет знак, и время торможения tт будет равным (9).
При тех же условиях- постоянстве моментов M и Мс и момента инерции I,
(10)
Время торможения tт от номинальной скорости w1=wном до скорости w2 =0 будет равна
(11)