ТЕМА № 23

ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ

23.1. Корпускулярные и волновые свойства частиц вещества

Французский физик Луи де Бройль в 1924 году пришел к выводу, что корпускулярно-волновой дуализм свойств характерен не только свету. Если по мере возрастания частоты света его волновые свойства все труднее обнаружить, то можно предположить существование еще более коротких волн, чем у γ- излучения, связанных каким-то образом с частицами вещества ― электронами, нейтронами, атомами, молекулами и т.д.

Де Бройль обобщил соотношение Pф=h/λ, предложив , что оно имеет универсальный характер для любых волновых процессов, связанных с частицами, обладающими импульсом Р:

𝛌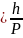 (23.1)

Формула (23.1) называется формулой де Бройля и является одним из соотношений, лежащих в основе современной физики.

Для частиц с массой m, движущейся со скоростью υ<c,

λ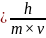 .(формула 2)

Если частица имеет кинетическую энергию К, то, учитывая, что , можно записать формулу 2 в виде

λ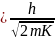 (формула 3)

В частности, для электрона, ускоряющегося в электрическом поле с разностью потенциалов ΔY, имеем 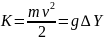. Подставим это выражение в формулу 3 и вычислим все постоянные, получим формулу, обычно применяемую в практических расчетах( [ΔY]-B,[λ]-10^-10м)

.

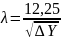Т.О. с каждым микрообьектом связывается, с одной стороны, корпускулярные характеристики-энергия Е и импульс Р, а с другой – волновые характеристики – частота V и длина волны λ .

Количественные характеристики, такие же, как для фотонов:

23.2. Опыты по дифракции электронов

Формула де Бройля, экспериментально подтверждалась в опытах К.Дэвиссона и Л.Джермера(1927), наблюдавших рассеяние электронов монокристаллами никеля.

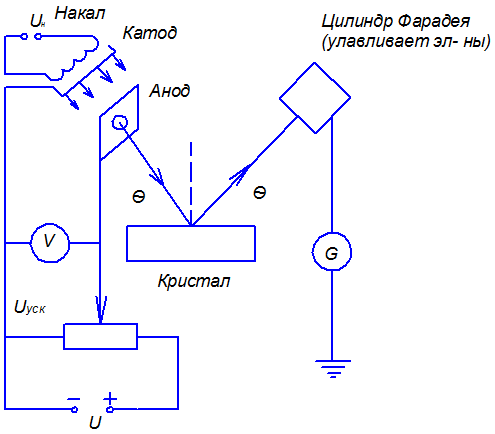
Схема опыта 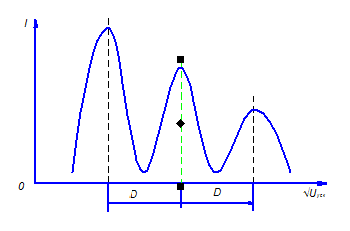Результаты опыта

Результаты опытов Дэвиссона и Джермера можно обьяснить, если привлечь идею де Бройля о волновых свойствах электронов.

Выразим скорость электрона через ускоряющее напряжение по формуле

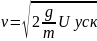
Теперь можно найти импульм и вычислить дебройлевскую длину волны:

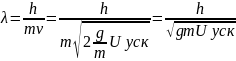
Если пучок электронов обладает волновыми свойствами, то он должен отражаться от кристалла так же, как и ренгеновское излучение, т.е. в соответствии с условиями Вульфа-Брэгга

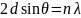(n=1,2,3,…)

Учитывая выражение для длины волны де Бройля, получаем

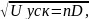
где - величина, являющаяся постоянной в условиях опыта.

Входящее в это соотношение ускоряющее напряжение 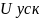соответствует максимумам отражения, т.к. именно к этим случаям относится условия Вульфа-Брэгга.

Как мы видим, значения , соответствующее соседним максимумам отражения, отстоят друг от друга на одинаковые расстояние D в соответствии с опытом.

Больше того, подстановка реальных числовых данных, соответствующих условиям опыта(значения d и θ), в полученную формулу для D дано прекрасное согласие с результатами опытов Дэвиссона и Джермера.

Таким образом, идея де Бройля о волновых свойствах частиц и количественное выражение этой идеи- формула де Бройля-получим блестящее подтверждение.