2. Световая волна

Свет (видимый свет) представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других - как поток особых частиц (фотонов). В начале книги излагается волновая оптика, т.е. круг явлений, в основе которых лежит волновая природа света. Совокупность явлений, обусловленных корпускулярной природой света, т.е. квантовой оптика, будет рассмотрена в конце книги.

В электромагнитной волне колеблются векторы и . Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие действия света вызываются колебаниями электрического вектора. В соответствии с этим мы будем в дальнейшем говорить о световом векторе, подразумевая под ним вектор напряженности электрического поля. О магнитном векторе световой волны мы упоминать почти не будем.

Модуль амплитуды светового вектора мы будем обозначать, как правило, буквой (иногда ). Соответственно измерение во времени и пространстве проекции светового вектора на направление, вдоль которого он колеблется, будет описываться уравнением

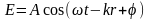. (1.18)

Здесь ― волновое число, 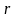― расстояние, отсчитываемое вдоль направления распространения световой волны и т.д.

2.1. Показатель преломления среды

Отношение скорост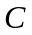и световой волны в вакууме к фазовой скорости 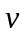в некоторой среде называется абсолютным показателем преломления этой среды и обозначается буквой . Таким образом,

(1.19)

С другой стороны согласно Максвеллу (1.5)

. (1.20)

Из выражений (1.19) и (1.20) имеем

(1.21)

Соотношение (1.21) называется законом Максвелла. Оно устанавливает связь между оптическими, электрическими и магнитными константами вещества.

Для среды, не обладающей магнитными свойствами, и практически можно считать, что

. (1.22)

Относительным показателем преломления двух сред (второй среды по отношению к первой) называется величина , равная отношению показателей преломления этих сред:

(1.23)

Для немагнитных сред

. (1.24)

Значения показателя преломления характеризуют оптическую плотность среды. Среда с большим показателем преломления является оптически более плотной, чем среда с меньшим показателем преломления Соответственно, среда с меньшим показателем преломления является оптически менее плотной, чем среда с большим показателем преломления .

2.2. Интенсивность света

Длины волн видимого света в вакууме заключены в пределах

(1.25)

В веществе длины световых волн будут иными. В случае колебаний частоты длина волны в вакууме равна . В среде, в которой фазовая скорость световой волны 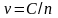, длина волны имеет значение 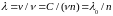. Таким образом, длина световой волны в среде с показателем преломления связана с длиной волны в вакууме соотношением

(1.26)

С учетом (1.26) аналогичное соотношение можно получить и для волнового числа

(1.27)

Здесь ― волновое число в вакууме.

Частоты видимых световых волн лежат в пределах

Гц. (1.27)

Частота изменений вектора плотности потока энергии, переносимой волной, будет еще больше (она равна ). Ни глаз, ни какой-либо иной приемник световой энергии не может уследить за столь частыми изменениями потока энергии, вследствие чего они регистрируют усредненный по времени поток. Модуль среднего по времени значения плотности потока энергии, переносимой световой волной, носит название интенсивности света 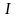в данной точке пространства. Плотность потока электромагнитной энергии определяется вектором Пойнтинга . Следовательно,

. (1.28)

Усреднение производится за время "срабатывания" прибора, которое, как отмечалось, много больше периода колебаний волны. Измеряется интенсивность либо в энергетических единицах (например в ваттах на квадратный метр). либо в световых единицах, носящих название "люмен на квадратный метр".

Модули амплитуд векторов и в электромагнитной волне связаны соотношением (1.10). Положив в этом соотношении 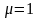, найдем

,

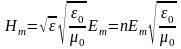где ― показатель преломления среды, в которой распространяется волна. Таким образом, пропорционально и :

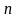. (1.29)

Модуль среднего значения вектора Пойнтинга пропорционален 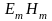. Поэтому можно написать, что

(1.30)

(коэффициент пропорциональности равен ). Следовательно, интенсивность света пропорциональна показателю преломления среды и квадрату амплитуды световой волны.

Заметим, что при рассмотрении распространении света в однородной среде можно считать, что интенсивность пропорциональна квадрату амплитуды световой волны:

(1.31)

Однако в случае прохождения света через границу раздела сред выражение для интенсивности, не учитывающее множитель , приводит к несохранению светового вектора.